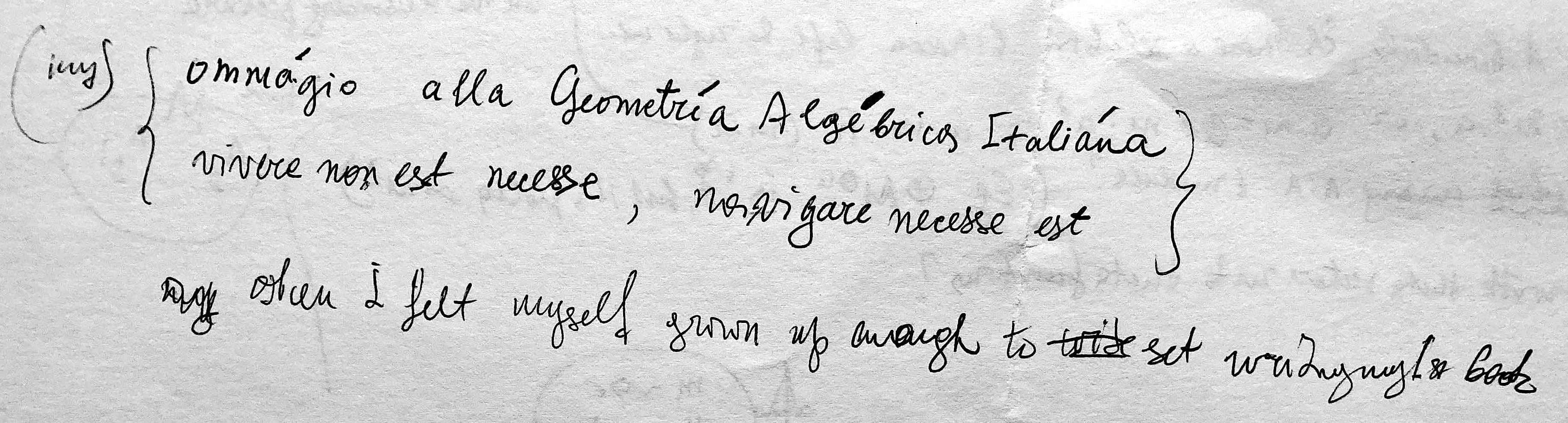Ognuno sta solo sul cuor della terra, trafitto da un raggio di sole: ed è subito sera. (Salvatore Quasimodo)1Everyone stands alone over the earth’s core, / pierced by a sun ray: / and immediately it’s nightfall.
Nostalgia, in Greek, is the pain of returning: the νόστος of the Homeric heroes trying to find their way back in a world forever altered. Return and remembrance are a painful illusion, our longing for a past that can speak to us in a familiar voice.
I promised him I would come in the spring. By the time I was done with my cancer treatment and able to travel again, I was four months too late. I ended up spending a week in his MPI office, looking through the writings he left behind: one week for an entire lifetime. That’s when I started writing this piece. On the small board outside the door of his office, along with his photograph and the cover pages of his recent preprints, he had posted a copy of Quasimodo’s poem Ed è subito sera (Figure 1). Indeed, even after a long life full of so many remarkable achievements, that final nightfall still comes very suddenly and unexpectedly. It still comes much too soon. There was still so much joy of life, of thought, so much energy and creativity left in him, up until the very end of his life.
I used to spend late night hours at the institute, in the eight years when I was his colleague at the MPI. Yuri and Xenia used to tease me when I would walk back to my office, instead of going home, as we were coming back from a concert or a movie and a dinner together. Yes, I used to work at the MPI late at night, but I had never before seen the dawn from the institute windows, like I am doing now every night. I am seeing it from his office windows: a beautiful sight of the first light of day on Bonn’s Münsterplatz. I use this time during the night, before anyone else comes in, to reflect on what all this had meant to me over the past twenty years, to read through stacks of his handwritten notes, to look through his books on the shelves – still where I remember them –, to experience the last remnants of his physical presence in the place where he spent the last thirty years of his life.
The oldest handwritten notes I came across in his office are in a small notebook dated 1965. They are notes about results from the Italian school of algebraic geometry: on the first page a commentary on a 1948 paper by Predonzan, Intorno agli giacenti sulla varietà intersezione completa di più forme (Figure 2). Just the previous evening I had found among the recent papers left on the desk of his home office a short note expressing his enthusiasm for the classical Italian algebraic geometry (Figure 3).
Two events in the 1960s influenced significantly his view of this field of mathematics: a visit to Pisa, during which he learned Italian, read Dante and an extensive combination of writings by Italian algebraic geometers, and the subsequent visit to Grothendieck at the IHES in Paris, which lead him to write what became the very first published paper on Grothendieck’s theory of motives [10 Yu. I. Manin, Correspondences, motifs and monoidal transformations. (in Russian) Mat. Sb. (N.S.) 77 (119), 475–507 (1968); English translation: Math. USSR Sb. 6, 439–470 (1968) ]. During the second half of the 20th century the field of algebraic geometry witnessed a sharp divide between the abstract categorical language of the Grothendieck approach, on one side, and the hands-on geometric example-driven approach that can be traced back to the older Italian school. We all know algebraic geometers who fall squarely into one or the other of these two camps, but fewer embrace both views simultaneously, finding ways to combine them with ease in their own work. Yuri always carried with him this simultaneous dual view of algebraic geometry that came to characterize his approach to the field.
By that time, Yuri was already widely famous for his proof, in 1963, of the Mordell Conjecture over function fields [9 Yu. I. Manin, Rational points on algebraic curves over function fields. (in Russian) Izv. Akad. Nauk SSSR Ser. Mat. 27, 1395–1440 (1963) ]. The conjecture establishes a relation between topological and arithmetic properties of curves: if the genus is , then the number of rational points is finite. The case over function fields can be restated in terms of a pencil of curves over a projective algebraic surface. The main tool involved in the proof is an abstract formulation of Picard–Fuchs equations in the form of a connection on a bundle whose fibers are de Rham cohomologies, and whose flat sections are the differential equations that govern the structure of period integrals [8 Yu. I. Manin, Algebraic curves over fields with differentiation. (in Russian) Izv. Akad. Nauk SSSR Ser. Mat. 22, 737–756 (1958); ]. It was Grothendieck who started calling this construction the Gauss–Manin connection. It has since then become a fundamental and widely applied tool in algebraic and arithmetic geometry.
Classical algebraic geometry works by Enriques, Segre, and especially Fano formed the background for his result with Iskovskih [6 V. A. Iskovskih and Yu. I. Manin, Three-dimensional quartics and counterexamples to the Lüroth problem. (in Russian) Mat. Sb. (N.S.) 86(128), 140–166 (1971); English translation: Math. USSR Sb. 15, 141–166 (1971) ] on the existence of smooth quartic threefolds that are unirational but not rational, which provided a negative answer to the Lüroth problem in 1971.
The beginning of the 1970s is also the time when he published his first book. When I felt myself grown up enough to set writing my first book, he says in the short note left on his home desk, alongside the words omaggio alla geometria algebrica italiana, homage to Italian algebraic geometry (Figure 3). The note also contains the Latin translation of Plutarch’s πλεῖν ἀνάγκη, ζῆν οὐκ ἀνάγκη (to sail is indispensable, to live is not). Yuri must have likely written it just weeks before his death. In Greek ἀνάγκη is necessity by way of fate. Yuri used to say that mathematics chooses us, not the other way around: to him it was fate, destiny, and indispensable vital need.
At the end of the introduction to the book Cubic forms [12 Yu. I. Manin, Cubic forms: Algebra, geometry, arithmetic. (in Russian) Izdatel’stvo “Nauka”, Moscow (1972); English translation: North-Holland, Amsterdam (1974) ], Yuri quotes works of Grothendieck, Segre, and Châtelet as main sources of inspiration. The book assembles a significant amount of Yuri’s work in algebraic geometry over the preceding years, combined into a beautiful narrative. What happens to the group law of elliptic curves when one moves up to rational points of a cubic surface? The surprising answer is non-associative commutative Moufang loops. The classical geometry of the lines on a cubic surface leads to a modern interpretation in terms of a birational invariant of the surface given by the Galois cohomology group (that can also be described in terms of Brauer groups), which can be computed from the partition of the lines into Galois orbits. The book is a treasure trove: minimal cubic surfaces and birational transformations, Brauer–Grothendieck group and Brauer equivalence via Azumaya algebras, and other intriguing connections between arithmetic and geometry.
Cubic forms was for a long time the only one of Yuri’s books I did not have. It is hard to find, and only last fall I was able to order a good copy from a bookseller. It did not come for a long time, and I assumed it had been lost in the mail. It was delivered to my home in the evening of January 7, the same day when Yuri died. Carl Gustav Jung (another interest Yuri and I shared) called these meaningful coincidences: random acausal events that happen to take place at crucial times in our lives and that our psyche therefore invests with meaning.
There are no more lights in the institute windows at night: there used to be plenty, not just mine, but the MPI was a different place at that time. I left in 2008. Yes, I left. It seemed like a good decision at the time – the MPI was changing and my job in California was attractive, but the years kept passing and I never quite felt like I had rooted my life elsewhere. My center of coordinates had stayed in this room, which is now about to disappear. I kept coming back, year after year.
We started working together almost immediately after I joined the MPI faculty in the summer of 2000. Yuri suggested that we revisit his theory of modular symbols [13 Yu. I. Manin, Parabolic points and zeta functions of modular curves. (in Russian) Izv. Akad. Nauk SSSR Ser. Mat. 36, 19–66 (1972); English translation: Math. USSR Izv. 6, 19–64 (1972) ] from a different perspective, related to noncommutative geometry and the “invisible boundary” of modular curves determined by the irrational points in the boundary of the upper half plane [26 Yu. I. Manin and M. Marcolli, Continued fractions, modular symbols, and noncommutative geometry. Selecta Math. (N.S.) 8, 475–521 (2002) ]. While the rational points, the cusps, have an algebro-geometric interpretation in terms of degenerations of elliptic curves to the multiplicative group, the irrational points can be regarded as degenerations that no longer exist algebro-geometrically but only as noncommutative tori. Limiting modular symbols exist at such invisible points, determined by an ergodic average of classical modular symbols, and the arithmetic contributions of this part of the geometry can be seen by expressing Mellin transforms of cusp forms in terms of quantities defined entirely on this boundary [26 Yu. I. Manin and M. Marcolli, Continued fractions, modular symbols, and noncommutative geometry. Selecta Math. (N.S.) 8, 475–521 (2002) ], leading to a more general formalism of modular shadows, Lévy functions, and Lévy–Mellin transforms [27 Yu. I. Manin and M. Marcolli, Modular shadows and the Lévy–Mellin ∞-adic transform. In Modular forms on Schiermonnikoog, Cambridge University Press, Cambridge, 189–238 (2008) ]. The role of noncommutative tori as non-algebro-geometric degenerations of elliptic curves and of the noncommutative boundary of modular curves as their moduli space was the source of Yuri’s real multiplication program [23 Yu. I. Manin, Real multiplication and noncommutative geometry (ein Alterstraum). In The legacy of Niels Henrik Abel, pp. 685–727, Springer, Berlin, Heidelberg (2004) ], based on the beautiful idea that noncommutative tori with real multiplication (non-trivial Morita self-equivalences) should play the role of the missing geometry behind the explicit class field theory problem for real quadratic fields, like elliptic curves with complex multiplication for the imaginary quadratic case. This promising program still remains unfulfilled.
Modular symbols, periods of modular forms, and -functions formed the central theme of a series of papers Yuri wrote in the 1970s, relating cusp forms and their period integrals and Hecke series. Results include explicit formulae for Hecke eigenvalues, algebraicity results for periods of cusp forms, -adic Hecke series through -adic measures associated to cusp forms and the -adic Mellin transform, an effective algorithm for the computation of the Tate–Shafarevich group of elliptic curves based on Mellin transforms of -functions and modular symbols. In the Helsinki ICM address [15 Yu. I. Manin, Modular forms and number theory. In Proceedings of the International Congress of Mathematicians (Helsinki, 1978), pp. 177–186, Academia Scientiarum Fennica, Helsinki (1980) ], Yuri summarizes several of these results, presenting as the central theme of number theory the interaction between the two classes of -functions, associated to varieties through cohomologies, and associated to modular and automorphic forms.
There are two extensive sets of handwritten notes I found in his office, one on Lévy functions and what was supposed to be our continuation of [26 Yu. I. Manin and M. Marcolli, Continued fractions, modular symbols, and noncommutative geometry. Selecta Math. (N.S.) 8, 475–521 (2002) ] and [27 Yu. I. Manin and M. Marcolli, Modular shadows and the Lévy–Mellin ∞-adic transform. In Modular forms on Schiermonnikoog, Cambridge University Press, Cambridge, 189–238 (2008) ], and one on the real multiplication project. Both were likely written in the mid-2000s, probably 2005 or 2006. We had frequent conversations at the time on all of these topics, but during those years I got diverted into other projects (perhaps unwisely handled in retrospect) and much remained undone: here is where the pain of returning becomes especially hard to bear.
But I am here again, night and day, going through these written remnants of Yuri’s work: many more sets of carefully organized handwritten notes, references he was reading along with them, drafts of papers, printouts of email exchanges, lecture notes for courses he taught in Moscow, at MIT, at the MPI, at Northwestern. I am reading through all of this, in whatever order the folders come into my hands: everything has already been sorted out, during these months after his death, when I still could not be here.
His work: it makes me think of the ocean, with big waves and deep currents. That’s what I see, as I go over folder after folder of manuscripts and notes, those huge waves of work stretching over the years. When I moved to Bonn from Boston in 2000, I arrived in time to catch the last years of the long wave of quantum cohomology and Frobenius manifolds, that started shortly after he had himself moved to the MPI from MIT in 1993, and that dominated his interests for a decade. His work with Kontsevich, starting in 1994 [7 M. Kontsevich and Yu. Manin, Gromov–Witten classes, quantum cohomology, and enumerative geometry. Comm. Math. Phys. 164, 525–562 (1994) ], set the foundation for the algebro-geometric form of quantum cohomology and Gromov–Witten invariants, a mathematical construction that originated in the physical theory of quantum strings propagating on a spacetime manifold. This string theory setting leads to a deformation of the usual product on the cohomology of algebraic varieties, where instead of counting the intersection points between cycles, one uses an appropriate counting of algebraic curves connecting them. This algebro-geometric counting requires the geometry of moduli spaces of stable maps and the delicate notion of virtual fundamental classes. The axiomatic treatment of Gromov–Witten invariants and quantum cohomology leads naturally to the study of Frobenius manifolds as the underlying structure (a notion originally introduced by Dubrovin), with diverse applications in singularity theory and integrable systems. A motivic viewpoint on quantum cohomology was developed in his work with Behrend [3 K. Behrend and Yu. Manin, Stacks of stable maps and Gromov–Witten invariants. Duke Math. J. 85, 1–60 (1996) ], where the moduli spaces of stable maps are shown to determine correspondences between the motive of a variety and the motives of moduli spaces of curves, giving rise to an action of the modular operad on motives. This large body of work on Frobenius manifolds, moduli spaces, and quantum cohomology culminated in his very extensive research monograph on the subject, published in 1999 [22 Yu. I. Manin, Frobenius Manifolds, Quantum Cohomology, and Moduli Spaces. Amer. Math. Soc. Colloq. Publ. 47, American Mathematical Society, Providence, RI (1999) ]. My gift for Yuri’s 65th birthday was a Frobenius manifolds conference.
The relation between algebraic geometry and physics is the deeper current underlying this long wave of work on quantum cohomology and Frobenius manifold structures. Yuri was the first to clearly demonstrate the importance of algebraic geometry for string theory with the 1986 results (in [18 Yu. I. Manin, Theta-function representation of the partition function of a Polyakov string. JETP Lett. 43, 204–206 (1986) ], and with Beilinson in [4 A. A. Beĭlinson and Yu. I. Manin, The Mumford form and the Polyakov measure in string theory. Comm. Math. Phys. 107, 359–376 (1986) ]) expressing the Polyakov measure of the bosonic string path integral in terms of moduli spaces of curves, theta-functions, Green functions considered by Faltings in the setting of Arakelov geometry, and holomorphic quadratic differentials. The interaction between algebraic geometry and string theory has deeply transformed, in the decades that followed, both the field of high energy physics and algebraic geometry itself.
At various times, Yuri proposed the idea that not only algebraic geometry, but also arithmetic geometry and number theory should play a fundamental role in physics [20 Yu. I. Manin, Reflections on arithmetical physics. In Conformal invariance and string theory (Poiana Braşov, 1987), pp. 293–303, Perspect. Phys., Academic Press, Boston, MA (1989) ]. One of our first joint papers proposed the use of -adic geometry in the AdS/CFT holographic correspondence of string theory [25 Yu. I. Manin and M. Marcolli, Holography principle and arithmetic of algebraic curves. Adv. Theor. Math. Phys. 5, 617–650 (2001) ], reinterpreting in holographic terms an earlier result of Yuri on the fiber at infinity of Arakelov geometry [21 Yu. I. Manin, Three-dimensional hyperbolic geometry as ∞-adic Arakelov geometry. Invent. Math. 104, 223–243 (1991) ]. This idea of a -adic form of the AdS/CFT correspondence became popular with physicists fifteen years later. I have to admit that Yuri’s paper on the fiber at infinity of Arakelov geometry [21 Yu. I. Manin, Three-dimensional hyperbolic geometry as ∞-adic Arakelov geometry. Invent. Math. 104, 223–243 (1991) ] is probably the single paper that was most influential in the development of my own view of mathematics, not only in terms of work directly inspired by it, but more generally in terms of exemplifying what I find beautiful and valuable in mathematical research. Along with the published version of that paper, I kept a copy of the unpublished preprint that preceded it [19 Yu. I. Manin, Closed fibers at infinity in Arakelov’s geometry (Christmas tale at R. Coleman’s seminar, November 1989). Preprint (1989) ], full of his heuristic explanations, drawings, and analogies that formed the background to the final polished result (Figure 4).
Within his overall geometrization program, envisioning algebraic geometry as a unifying language in number theory, physics, and information theory, another large wave of work one comes across is the one that happened in the 1980s and early 1990s, encompassing the geometry of Yang–Mills instantons, supergeometry, and symmetries of quantum spaces. The ADHM (Atiyah–Drinfeld–Hitchin–Manin) construction and classification of Yang–Mills instantons on the -sphere is certainly the most famous result of this period [1 M. F. Atiyah, N. J. Hitchin, V. G. Drinfel’d and Yu. I. Manin, Construction of instantons. Phys. Lett. A 65, 185–187 (1978) ]. Solutions of Yang–Mills equations on -dimensional manifolds became, some years later, a major tool in low-dimensional topology, in the form of Donaldson invariants. Yuri’s extensive development of an algebro-geometric formulation of supergeometry was motivated by his interest in the physical theories of supergravity and supersymmetric Yang–Mills, for which he gave a precise mathematical formulation. A broad overview of the developments in mathematical physics, around the topics of Yang–Mills instantons, Penrose’s twistors, and supergeometry, obtained by him and his students, is presented in his book Gauge field theory and complex geometry [17 Yu. I. Manin, Gauge field theory and complex geometry. (in Russian) Nauka, Moscow (1984); English translation: Grundlehren der mathematischen Wissenschaften 289, Springer-Verlag, Berlin (1988) ]. Work with Kuperschmidt and Lebedev on integrable systems focused on the hierarchy of higher hydrodynamic equations of Benney type. In this context he also introduced the noncommutative residue of pseudodifferential operators, generalized by his student Wodzicki. After Drinfeld introduced quantum groups, Yuri showed that they can be realized as symmetries of quantum spaces, a natural point of view from the perspective of both physics and noncommutative geometry.
Yuri was the first person who suggested the idea of quantum computing, in his 1980 book Computable and uncomputable [14 Yu. I. Manin, Computable and noncomputable. (in Russian) Cybernetics, Soviet. Radio, Moscow (1980) ] (Figure 5), a good two years before Feynman made the same suggestion along similar lines of thought.
In the same period he promoted in his seminar the importance of algebro-geometric constructions in the theory of classical error-correcting codes (first used by Goppa in 1981), a topic that his students Tsfasman and Vlăduţ then widely developed. He introduced in [16 Yu. I. Manin, What is the maximum number of points on a curve over 𝑭2? J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28, 715–720 (1982) ] the asymptotic bound in the geography of error-correcting codes, relating the asymptotic theory of codes to the problem of constructing algebraic curves with sufficiently many algebraic points over finite fields. His impact on the theory of information epitomizes how topics that have by now become huge fields of research had germinated very early inside his mind: nowadays algebro-geometric codes lie at the heart of the edifice of cryptography and quantum information has become an enormous landscape, stretching across mathematics, physics, and computer science.
The themes of computability, of classical and quantum information, and of error-correcting codes resurfaced frequently in his later work, and became a very significant interest in the last years of his life, including a considerable part of our own joint work, for instance [28 Yu. Manin and M. Marcolli, Kolmogorov complexity and the asymptotic bound for error-correcting codes. J. Differential Geom. 97, 91–108 (2014) , 30 Yu. I. Manin and M. Marcolli, Computability questions in the sphere packing problem. (2022) arXiv:2212.05119]. This is another example of what I see as the deep currents in Yuri’s work, those long visions that stretched through the decades, acting as a background structure, and emerging periodically to the forefront of his research activities.
Another long-term current in Yuri’s work is Diophantine equations and the properties of rational points of varieties. The Hasse principle asserts that the existence of rational points of a variety over a number field can be deduced from the existence of points over all the non-Archimedean and Archimedean completions (that is, one can go from local to global solutions). Yuri first showed that the Brauer–Grothendieck group determines an obstruction (the Brauer–Manin obstruction) to the Hasse principle [11 Yu. I. Manin, Le groupe de Brauer–Grothendieck en géométrie diophantienne. In Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1, pp. 401–411, Gauthier-Villars, Paris (1971); also in: Selected papers of Yu. I. Manin, World Sci. Ser. 20th Century Math. 3, pp. 191–201, World Scientific Publishing, Singapore (1996) ]. The existence of this general obstruction changed the perspective on Diophantine problems, and the understanding of local-to-global principles. His extensive investigation of rational points of bounded height on cubic surfaces brought him to develop a broad research program relating geometry and topology of varieties to Diophantine properties. Varieties with ample canonical class (intuitively, hyperbolic or negatively curved, like the algebraic curves of genus ) are expected to have fewer rational points, lying on lower-dimensional submanifolds. For large anticanonical class (elliptic or positively curved, like Fano varieties) one expects many rational points. Work with Batyrev [2 V. V. Batyrev and Yu. I. Manin, Sur le nombre des points rationnels de hauteur borné des variétés algébriques. Math. Ann. 286, 27–43 (1990) ] showed two important aspects of the structure of rational points: the presence of accumulating subvarieties and the linear growth of the number of points with bounded anticanonical height on the complement of accumulating subvarieties (Manin’s linear growth conjecture). A series of papers in the late 1980s and early 1990s, starting with [5 J. Franke, Yu. I. Manin and Yu. Tschinkel, Rational points of bounded height on Fano varieties. Invent. Math. 95, 421–435 (1989) ] with Franke and Tschinkel, provided evidence for the explicit form of the asymptotic behavior for the number of points of bounded height for varieties over number fields, in the ample anticanonical case, with . During the last two years of his life, Yuri became interested in the possibility of categorifying the height zeta function, so as to encode, in the form of scissor-congruence type relations, the presence of accumulating subvarieties, and suggested the relevance of homotopy-theoretic methods to this goal [31 Yu. I. Manin and M. Marcolli, Homotopy spectra and Diophantine equations. (2021) arXiv:2101.00197; to appear in The Literature and History of Mathematical Science, International Press, Boston ]. He very much considered this a line of thought that he meant to continue developing.
There are so many other things left in these folders, in his office. It’s a beautiful large office, with a lot of light, windows overlooking the central Münsterplatz, a beautiful place from where to watch the ending of a world (Figure 7). All of this will be gone soon, though I am trying to help making it digitally available at some point in the future. Among the things I keep finding: a typewritten manuscript of the Strugatsky brothers (which appears to be unpublished to my inexperienced eyes), writings on a variety of subjects (including the original manuscripts of several essays of [24 Yu. I. Manin, Les mathématiques comme métaphore. Les Belles Lettres, Paris (2021) ]), and especially poetry, his own as well as his translations of other poets. Poetry is everywhere: it forms a pervasive ubiquitous subtext both in and around his mathematical thoughts.
I came across some of his old writings in linguistics (Figure 6). I often go by as a linguist these days, but our paths to the subject have been very different and in many ways complementary. He wrote about glottogenesis and protolanguages (like the hypothetical Nostratic) and about psycho-linguistics. He was interested in mathematics as language. I have been interested in language as mathematics, but he often voiced criticism of generative linguistics, as an excess of abstraction away from the more intricate specific functioning of languages. On Christmas day of 2015, as Yuri and I met to work on our own joint paper in linguistics [29 Yu. I. Manin and M. Marcolli, Semantic spaces. Math. Comput. Sci. 10, 459–477 (2016) ], I received an email from Chomsky about my work on syntactic parameters. Speak of the devil… – I told Yuri as I showed it to him. It remained an inside joke between us, whenever the topic of linguistics came up in our discussions. In another of those uncanny Jungian coincidences, Noam reappeared in my life on the same day when the MPI held the memorial service for Yuri, in January, to start our currently ongoing linguistic collaboration. Months after Yuri’s death, it is still impossible for me to return to thinking about mathematics. He was in every part of mathematics I ever happened to think about (gauge theory, noncommutative geometry, motives, mathematical physics…), and now everything hurts. I always remained an outsider to the world of mathematicians and the one who was able to make me feel at home there is now forever gone. I will return to it one day, probably, but right now I just cannot. By a strange twist of fate, the formal mathematical abstraction of generative linguistics that Yuri used to criticize turned out to be now the only thing that made it possible for me to continue working during the past few months.
I’ll take the liberty of ending this piece on a personal note. This is the third time I am asked to write some form of obituary, reminiscence, tribute, commentary on Yuri’s death: making a public spectacle of the pain of losing the closest friend I ever had, navigating the acceptable boundary of words. It hurts, every time more. Because I miss him more and more as the months are passing. Because I am here trying to invent implausible motivations for why the show must go on, for why I ought to keep doing the things I used to do, without a main reason for why I did them. I am not requesting that you would all stop asking me: I understand it that, as a long term collaborator and close personal friend, it is my duty to do this kind of writing in his memory. I would just like you to reflect on how duty becomes a proxy for pain when the latter has no proper venue of expression, and on how much we lose as a community if we try to separate our mathematical achievements from the deeper core we stand on, the value of our humanity.
ἀλλά με κακκῆαι σὺν τεύχεσιν, ἅσσα μοι ἔστιν, σῆμά τέ μοι χεῦαι πολιῆς ἐπὶ θινὶ θαλάσσης (Homer, Odyssey, XI, 74–75)2But burn me with my armor and all my belongings, and drop a sign of me on the shore of the grey sea.
- 1
Everyone stands alone over the earth’s core, / pierced by a sun ray: / and immediately it’s nightfall.
- 2
But burn me with my armor and all my belongings, and drop a sign of me on the shore of the grey sea.
References
- M. F. Atiyah, N. J. Hitchin, V. G. Drinfel’d and Yu. I. Manin, Construction of instantons. Phys. Lett. A 65, 185–187 (1978)
- V. V. Batyrev and Yu. I. Manin, Sur le nombre des points rationnels de hauteur borné des variétés algébriques. Math. Ann. 286, 27–43 (1990)
- K. Behrend and Yu. Manin, Stacks of stable maps and Gromov–Witten invariants. Duke Math. J. 85, 1–60 (1996)
- A. A. Beĭlinson and Yu. I. Manin, The Mumford form and the Polyakov measure in string theory. Comm. Math. Phys. 107, 359–376 (1986)
- J. Franke, Yu. I. Manin and Yu. Tschinkel, Rational points of bounded height on Fano varieties. Invent. Math. 95, 421–435 (1989)
- V. A. Iskovskih and Yu. I. Manin, Three-dimensional quartics and counterexamples to the Lüroth problem. (in Russian) Mat. Sb. (N.S.) 86(128), 140–166 (1971); English translation: Math. USSR Sb. 15, 141–166 (1971)
- M. Kontsevich and Yu. Manin, Gromov–Witten classes, quantum cohomology, and enumerative geometry. Comm. Math. Phys. 164, 525–562 (1994)
- Yu. I. Manin, Algebraic curves over fields with differentiation. (in Russian) Izv. Akad. Nauk SSSR Ser. Mat. 22, 737–756 (1958);
- Yu. I. Manin, Rational points on algebraic curves over function fields. (in Russian) Izv. Akad. Nauk SSSR Ser. Mat. 27, 1395–1440 (1963)
- Yu. I. Manin, Correspondences, motifs and monoidal transformations. (in Russian) Mat. Sb. (N.S.) 77 (119), 475–507 (1968); English translation: Math. USSR Sb. 6, 439–470 (1968)
- Yu. I. Manin, Le groupe de Brauer–Grothendieck en géométrie diophantienne. In Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 1, pp. 401–411, Gauthier-Villars, Paris (1971); also in: Selected papers of Yu. I. Manin, World Sci. Ser. 20th Century Math. 3, pp. 191–201, World Scientific Publishing, Singapore (1996)
- Yu. I. Manin, Cubic forms: Algebra, geometry, arithmetic. (in Russian) Izdatel’stvo “Nauka”, Moscow (1972); English translation: North-Holland, Amsterdam (1974)
- Yu. I. Manin, Parabolic points and zeta functions of modular curves. (in Russian) Izv. Akad. Nauk SSSR Ser. Mat. 36, 19–66 (1972); English translation: Math. USSR Izv. 6, 19–64 (1972)
- Yu. I. Manin, Computable and noncomputable. (in Russian) Cybernetics, Soviet. Radio, Moscow (1980)
- Yu. I. Manin, Modular forms and number theory. In Proceedings of the International Congress of Mathematicians (Helsinki, 1978), pp. 177–186, Academia Scientiarum Fennica, Helsinki (1980)
- Yu. I. Manin, What is the maximum number of points on a curve over 𝑭2? J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28, 715–720 (1982)
- Yu. I. Manin, Gauge field theory and complex geometry. (in Russian) Nauka, Moscow (1984); English translation: Grundlehren der mathematischen Wissenschaften 289, Springer-Verlag, Berlin (1988)
- Yu. I. Manin, Theta-function representation of the partition function of a Polyakov string. JETP Lett. 43, 204–206 (1986)
- Yu. I. Manin, Closed fibers at infinity in Arakelov’s geometry (Christmas tale at R. Coleman’s seminar, November 1989). Preprint (1989)
- Yu. I. Manin, Reflections on arithmetical physics. In Conformal invariance and string theory (Poiana Braşov, 1987), pp. 293–303, Perspect. Phys., Academic Press, Boston, MA (1989)
- Yu. I. Manin, Three-dimensional hyperbolic geometry as ∞-adic Arakelov geometry. Invent. Math. 104, 223–243 (1991)
- Yu. I. Manin, Frobenius Manifolds, Quantum Cohomology, and Moduli Spaces. Amer. Math. Soc. Colloq. Publ. 47, American Mathematical Society, Providence, RI (1999)
- Yu. I. Manin, Real multiplication and noncommutative geometry (ein Alterstraum). In The legacy of Niels Henrik Abel, pp. 685–727, Springer, Berlin, Heidelberg (2004)
- Yu. I. Manin, Les mathématiques comme métaphore. Les Belles Lettres, Paris (2021)
- Yu. I. Manin and M. Marcolli, Holography principle and arithmetic of algebraic curves. Adv. Theor. Math. Phys. 5, 617–650 (2001)
- Yu. I. Manin and M. Marcolli, Continued fractions, modular symbols, and noncommutative geometry. Selecta Math. (N.S.) 8, 475–521 (2002)
- Yu. I. Manin and M. Marcolli, Modular shadows and the Lévy–Mellin ∞-adic transform. In Modular forms on Schiermonnikoog, Cambridge University Press, Cambridge, 189–238 (2008)
- Yu. Manin and M. Marcolli, Kolmogorov complexity and the asymptotic bound for error-correcting codes. J. Differential Geom. 97, 91–108 (2014)
- Yu. I. Manin and M. Marcolli, Semantic spaces. Math. Comput. Sci. 10, 459–477 (2016)
- Yu. I. Manin and M. Marcolli, Computability questions in the sphere packing problem. (2022) arXiv:2212.05119
- Yu. I. Manin and M. Marcolli, Homotopy spectra and Diophantine equations. (2021) arXiv:2101.00197; to appear in The Literature and History of Mathematical Science, International Press, Boston
Cite this article
Matilde Marcolli, Pierced by a sun ray. Eur. Math. Soc. Mag. 129 (2023), pp. 25–31
DOI 10.4171/MAG/159