RICAM, the Johann Radon Institute for Computational and Applied Mathematics

1 Introduction: The structure of RICAM

The Johann Radon Institute for Computational and Applied Mathematics (RICAM) was founded in 2003 by Heinz Engl, who is now acting as the Rector of the University of Vienna, with the goal of establishing an internationally visible and successful research institute in the field of applied mathematics. Since then, RICAM has carried out basic research in computational and applied mathematics according to highest international standards and has emphasized interdisciplinary cooperation between its workgroups and with institutions with similar scope and universities around the globe. The researchers also cooperate with other disciplines, in particular within the framework of Special Semesters on topics of major current interest. One of the institute’s goals is to support young scientists. Indeed, the positions at the institute are usually for PhD students and PostDocs, and most of the members are young scientists who are in a stage of their career between the very beginning of their doctorate and the final step of obtaining a permanent position at a university or another research institution. The leaders of the work groups, which usually comprise 2–10 members, are typically university professors in Austrian universities. Through its position as the biggest mathematical non-university institute in Austria, through its work, and by its efforts in public outreach, RICAM promotes the role of mathematics in science, industry, and society.

RICAM currently consists of the following work groups with their corresponding leaders:

• Computational Methods for PDEs led by Ulrich Langer/Herbert Egger (Johannes Kepler University Linz),

• Geometry in Simulations led by Bert Jüttler (Johannes Kepler University Linz),

• Inverse Problems and Mathematical Imaging led by Otmar Scherzer (University of Vienna),

• Mathematical Data Science led by Philipp Grohs (University of Vienna),

• Mathematical Methods in Medicine and Life Sciences led by Luca Gerardo-Giorda (Johannes Kepler University Linz),

• Optimization and Optimal Control led by Karl Kunisch (Karl Franzens University Graz),

• Symbolic Computation led by Josef Schicho (Johannes Kepler University Linz),

• Transfer Group led by Ronny Ramlau (Johannes Kepler University Linz),

• Applied Discrete Mathematics and Cryptography led by Arne Winterhof (RICAM),

• Multiscale Modeling and Simulation of Crowded Transport in the Life and Social Sciences led by Marie-Therese Wolfram (University of Warwick), being phased out in 2021,

• Multivariate Algorithms and Quasi-Monte Carlo Methods led by Peter Kritzer (RICAM).

Prof. Heinz Engl was the first Director of the Institute until the end of 2011, when he became Rector of the University of Vienna.

Currently, the institute is led by Managing Director Prof. Ronny Ramlau and Deputy Director Prof. Karl Kunisch.

In the following sections, we would like to present selected recent research activities at RICAM.

2 Scientific machine learning

The usage of (data-driven) machine learning methods to tackle model-based problems, for example from the natural sciences, has recently evolved into a promising research area often termed “scientific machine learning”. In this section we describe partly related efforts in this direction by the two research groups “Mathematical Data Science” and “Optimization and Optimal Control”.

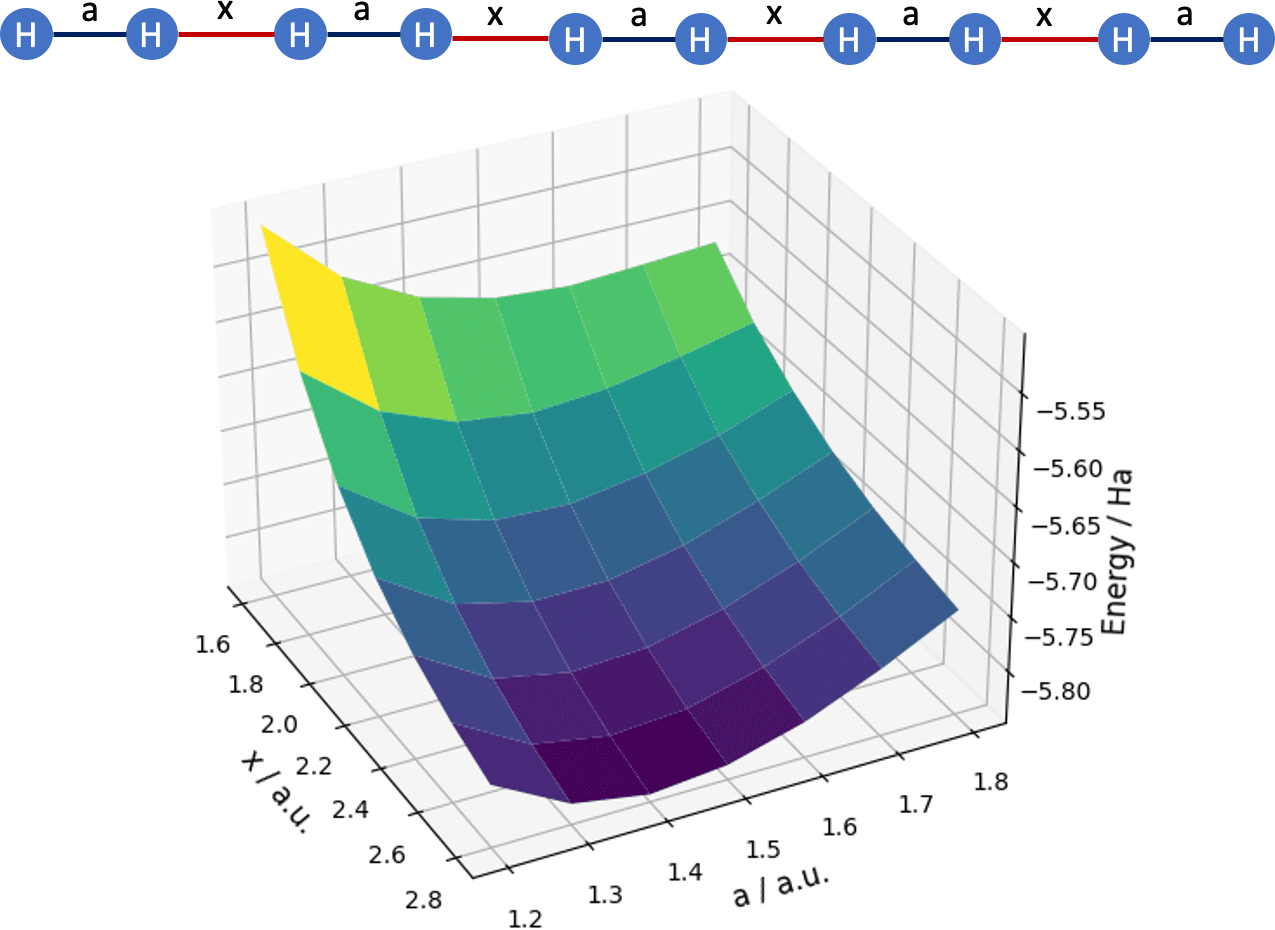
The group “Mathematical Data Science” represents the area of data science, particularly in relation to different aspects of applied mathematics. Its research is motivated by interdisciplinary applications and ranges from theory over algorithm development to the solution of real-world problems. A particular focus is currently put on the use and analysis of deep learning methods for the numerical solution of mostly high dimensional partial differential equations (PDEs) that are burdened by the curse of dimensionality in the sense that the computational complexity of most known algorithms scales at least exponentially in the underlying problem dimension. Prominent examples include the Black–Scholes (BS) PDE from computational finance, the Hamilton–Jacobi–Bellmann (HJB) PDEs arising from stochastic optimal control problems, or the many-electron Schrödinger equation from computational chemistry. For BS PDEs and certain nonlinear HJB PDEs we were recently able to prove that neural networks are capable of representing their solutions without incurring the curse of dimensionality [⁠9⁠ P. Grohs and L. Herrmann, Deep neural network approximation for high-dimensional parabolic Hamilton–Jacobi–Bellman equations. arXiv:2103.05744 (2021) , ⁠10⁠ P. Grohs, F. Hornung, A. Jentzen and P. Von Wurstemberger. A proof that artificial neural networks overcome the curse of dimensionality in the numerical approximation of Black–Scholes partial differential equations. Memoirs of the AMS, to appear (2020) ], and that such solutions can be numerically found by solving an empirical risk minimization (ERM) problem of a size scaling only polynomially in the problem dimension [⁠3⁠ J. Berner, P. Grohs and A. Jentzen, Analysis of the generalization error: empirical risk minimization over deep artificial neural networks overcomes the curse of dimensionality in the numerical approximation of Black–Scholes partial differential equations. SIAM J. Math. Data Sci.2, 631–657 (2020) ]. While the analysis of the computational complexity of the ERM problem remains wide open, there are some empirical results suggesting that its scaling does not suffer from the curse of dimensionality either, see [⁠2⁠ J. Berner, M. Dablander and P. Grohs, Numerically solving parametric families of high-dimensional Kolmogorov partial differential equations via deep learning. In Advances in Neural Information Processing Systems, volume 33, pages 16615–16627, edited by H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan and H. Lin, Curran Associates, Inc. (2020) ] and Figure ⁠3⁠. In another direction, we investigate the numerical solution of the many-electron Schrödinger equation using a deep learning based Quantum Monte Carlo ansatz. We show that a judicious weight sharing strategy enables the efficient computation of potential energy surfaces with chemical accuracy, see [⁠15⁠ M. Scherbela, R. Reisenhofer, L. Gerard, P. Marquetand and P. Grohs, Solving the electronic Schrödinger equation with weight-sharing deep neural networks for multiple nuclear geometries. arXiv:2105.08351 (2021) ] and Figure ⁠4⁠. We see that the use of modern machine learning methods for problems in scientific computing has the potential to overcome the curse of dimensionality for several important problems arising for example in computational finance, computational chemistry or optimal control. It therefore presents exciting opportunities to render previously intractable problems in these fields feasible. The extent to which this potential can be fully realized will constitute a central topic in future work.

The “Optimization and Optimal Control” group combines techniques from scientific machine learning with efforts to efficiently solve deterministic closed loop optimal control problems governed by partial differential equations, and problems in computer vision and medical imaging.

In [⁠6⁠ S. Dolgov, D. Kalise and K. K. Kunisch, Tensor decomposition methods for high-dimensional Hamilton–Jacobi–Bellman equations. SIAM J. Sci. Comput.43, A1625–A1650 (2021) ] a tensor decomposition approach for the solution of high-dimensional, fully nonlinear HJB equations arising in deterministic optimal feedback control of nonlinear dynamics is presented. It combines a tensor train approximation for the value function with a Newton-like iterative method for the solution of the resulting nonlinear system. In numerical tests the tensor approximation leads to a polynomial scaling with respect to the dimension, thus partially circumventing the curse of dimensionality. In an alternative approach [⁠13⁠ K. Kunisch and D. Walter, Semiglobal optimal feedback stabilization of autonomous systems via deep neural network approximation. ESAIM Control Optim. Calc. Var.27, Paper No. 16 (2021) ], rather than obtaining the feedback from the HJB equation directly, the feedback gains are approximated by neural networks, which are trained by open loop optimal controls. A third promising approach for the computation of high-dimensional optimal feedback laws is based on sparse regression exploiting the control-theoretical link between HJB equations and first-order optimality conditions via Pontryagin’s Maximum Principle [⁠1⁠ B. Azmi, D. Kalise and K. Kunisch, Optimal feedback law recovery by gradient-augmented sparse polynomial regression. Journal of Machine Learning Research, 22, 1–32 (2021) ]. Combined with model reduction techniques these methods have the potential of solving closed loop optimal control for complex partial differential equations. In another line of research [⁠7⁠ A. Effland, E. Kobler, K. Kunisch and T. Pock, Variational networks: an optimal control approach to early stopping variational methods for image restoration. J. Math. Imaging Vision62, 396–416 (2020) ], variational formulations of mathematical imaging problems are combined with deep learning techniques by introducing a data-driven total deep variation regularizer. We take advantage of the well-known phenomenon that typically the best image quality is achieved when the gradient flow process is stopped before converging to a stationary point. This paradox originates from a trade-off between optimization and modeling errors of the underlying variational model. An optimal stopping time is introduced, which is learned from data by means of an optimal control approach.

3 Inverse problems in science and industry

For many years, Linz has been a center of research in the area of “Inverse Problems”. Given – possibly noisy – measured data $y$, the goal of this research area is the development and analysis of methods that allow for a reconstruction of the underlying quantity $x$ using a suitable model $F$ that connects $y$ and $x$. This results in the task of solving a (possible) nonlinear operator equation $F(x)=y$. In many applications of interest the solution $x$ of the operator equation does not depend continuously on the data $y$, and requires the use of regularization techniques for a stable reconstruction [⁠8⁠ H. W. Engl and R. Ramlau. Regularization of inverse problems. In Encyclopedia of Applied and Computational Mathematics, edited by B. Engquist, Springer, Heidelberg (2015) ]. A well known example is Computerized Tomography (CT), where the measured damping of x-rays passing through a body is used to reconstruct the density distribution of the body. In this case, the connection between the density and the data is given by the Radon transform $R$ [⁠14⁠ R. Ramlau and O. Scherzer (eds.), The Radon transform. The First 100 Years and Beyond. Radon Ser. Comput. Appl. Math. 22, De Gruyter, Berlin (2019) ].

An active research area of the “Inverse Problems and Imaging Group” concerns the analysis and implementation of regularization methods, in particular total variation (TV) regularization (Figure ⁠5⁠) and tomographic inversions with uncertainties in the model (cf., e.g., [⁠12⁠ J. A. Iglesias and G. Mercier, Influence of dimension on the convergence of level-sets in total variation regularization. ESAIM Control Optim. Calc. Var.26, Paper No. 52 (2020) ]). One particular application of the latter is 3D visualization of optically and acoustically trapped particles from recorded diffraction images.

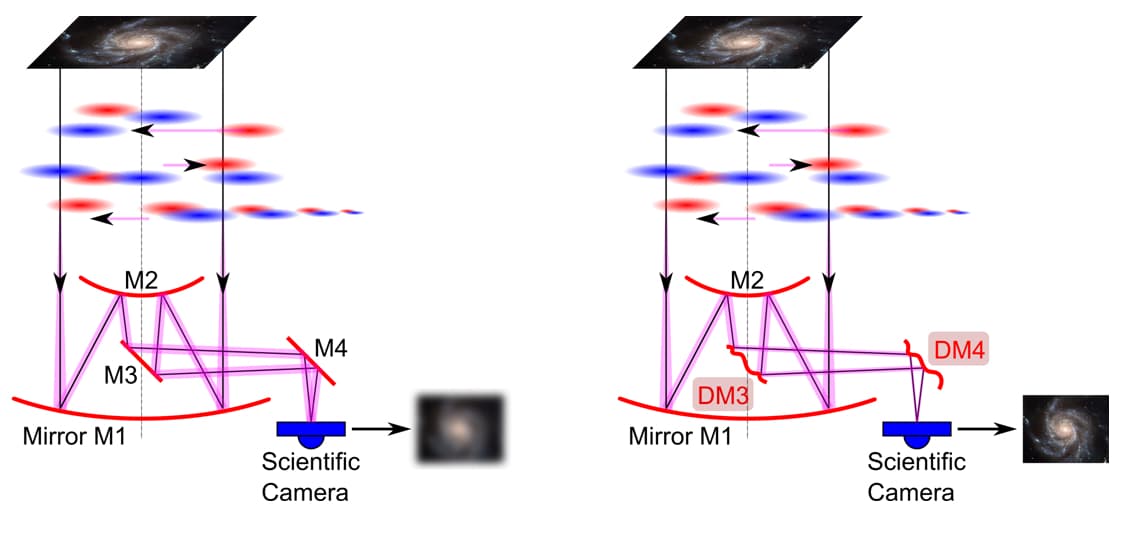
The “Transfer Group” is involved in several research projects with industry as well as other branches of science, with the goal of developing state of the art mathematical methods for applications. The group has a very tight collaboration with the “Inverse Problems and Imaging Group” within the special research program (SFB) Tomography across the Scales, which is formed by a group of researchers from mathematics, physics, astronomy and medical engineering. The Transfer Group has been particularly active in the field of Adaptive Optics (AO). AO was initially invented for the correction of degraded images from astronomical images, caused by turbulences in the atmosphere above earth-bound telescopes. To this end, incoming wavefront data from reference guide stars is measured by a wavefront sensor, and the reconstructed wavefront is used to compute an appropriate shape of deformable mirrors that are employed to correct the science images of the telescope (Figure ⁠6⁠). The whole correction process involves a series of mathematical tasks, e.g., modeling, analyzing and simulation of wavefront sensor devices, stable reconstruction of wavefronts from measured data [⁠11⁠ V. Hutterer, R. Ramlau and I. Shatokhina, Real-time adaptive optics with pyramid wavefront sensors: part I. A theoretical analysis of the pyramid sensor model. Inverse Problems35, 045007 (2019) ], reconstruction of the turbulence distribution above the telescope, optimal control of the correction of the deformable mirrors and computation of the overall Point Spread function of the observation. All the computations involved in this process must be done in real time, as the atmosphere changes every few milliseconds. RICAM is a partner of the European consortia developing the instruments METIS and MICADO [⁠5⁠ R. Davies, J. Alves, R. Ramlau, R. Wagner, V. Hutterer, J. Niebsch et al., The MICADO first light imager for the ELT: overview, operation, simulation. In Proceedings of the SPIE Astronomical Telescopes and Instrumentation Conference, Vol. 10702 (Austin, Texas, June 2018): Ground-based and Airborne Instrumentation for Astronomy VII, edited by C. J. Evans, L. Simard and H. Takami, SPIE, 570–581 (2018) ] for the Extremely Large Telescope of the European Southern Observatory (ESO), focusing on developing methods and software for its AO systems.

More recently, AO systems have also been used for image improvement in Ophthalmology and Microscopy. Within the aforementioned SFB, the Transfer Group works, in cooperation with the Medical University of Vienna, on the development of methods for AO systems in ophthalmic OCT systems that achieve an improved imaging quality of, e.g., the human retina, see Figure ⁠7⁠.

4 Cooperations between groups

As visible from the research work presented above, RICAM is more than just the sum of its individual work groups; cooperations between the groups and an atmosphere of creativity and innovation are among the strengths of the institute. Another is the special mix of mathematical disciplines present at RICAM. Apart from the groups highlighted in the previous sections, there is a group working on computational methods for PDEs, which has been led by Ulrich Langer until this year, and which is now in a transition phase after which it will be taken over by Langer’s successor, Herbert Egger. The group will focus on the development, analysis, and efficient realization of numerical methods for the simulation of coupled and multiscale phenomena in physics, engineering, and material and life sciences. Tight collaborations and synergies with several existing RICAM groups can be expected. In particular, this group is strongly connected to the “Geometry in Simulations” group, led by Bert Jüttler.

What is more, in contrast to several other large mathematics institutes, RICAM has a very strong and productive group working on symbolic computation, algebra, and combinatorics. A recent addition to the work groups is a team led by Luca Gerardo-Giorda focusing on applications to the life sciences. Further teams working on cryptography, simulation of crowded transport, and quasi-Monte Carlo methods round off the picture.

5 Special Semesters

RICAM Special Semesters attract world leaders in their respective research fields, and are the starting point for many international cooperations with RICAM scientists. Furthermore, they contribute significantly to the international visibility of the institute and to the exchange of the newest trends and developments. In general, at least one group leader, one other member of a group, and one member of the administrative staff are responsible for the organization of each Special Semester, frequently in cooperation with leading scientists from international research institutions. RICAM Special Semesters regularly attract around 200–300 guests. These may be either short term guests, who usually attend selected workshops, or long-term guests staying for longer periods during the Special Semester. The next Special Semester, “Tomography Across the Scales”, will be held in the fall of 2022, subject to positive developments with respect to the current global pandemic.

Philipp Grohs is professor at the University of Vienna and group leader at RICAM. His main research interests are in numerical analysis, signal processing, and mathematics of machine learning. He was awarded the ETH Latsis Prize and selected for an Alexander-von-Humboldt Professorship award. philipp.grohs@ricam.oeaw.ac.at Peter Kritzer is leading the RICAM work group “Multivariate Algorithms and Quasi-Monte Carlo Methods”. His research interests include high-dimensional numerical integration, function approximation, and information-based complexity. He received the Prize for Achievement in IBC in 2015. peter.kritzer@ricam.oeaw.ac.at Karl Kunisch is professor emeritus at the Karl-Franzens University Graz and group leader at RICAM. He is an applied mathematician whose main research interests lie in control and optimization in the context of partial differential equations. He was awarded an ERC advanced grant, and received the W. T. and Adalia Reid Prize. karl.kunisch@ricam.oeaw.ac.at Ronny Ramlau is professor for Industrial Mathematics at the Johannes Kepler University Linz and director of RICAM. His main research is on inverse problems and imaging, with a focus on astronomical and medical applications. Additionally, he is involved in several cooperations with industrial partners. ronny.ramlau@ricam.oeaw.ac.at Otmar Scherzer is professor at the University of Vienna and group leader at RICAM. He is working in applied mathematics, with a special focus on inverse problems and computational microscopic imaging. Furthermore, he is the editor-in-chief of the flagship journal “Inverse Problems”. otmar.scherzer@univie.ac.at

References

1. B. Azmi, D. Kalise and K. Kunisch, Optimal feedback law recovery by gradient-augmented sparse polynomial regression. Journal of Machine Learning Research, 22, 1–32 (2021)
2. J. Berner, M. Dablander and P. Grohs, Numerically solving parametric families of high-dimensional Kolmogorov partial differential equations via deep learning. In Advances in Neural Information Processing Systems, volume 33, pages 16615–16627, edited by H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan and H. Lin, Curran Associates, Inc. (2020)
3. J. Berner, P. Grohs and A. Jentzen, Analysis of the generalization error: empirical risk minimization over deep artificial neural networks overcomes the curse of dimensionality in the numerical approximation of Black–Scholes partial differential equations. SIAM J. Math. Data Sci.2, 631–657 (2020)
4. E. F. Brunner, I. Shatokhina, M. F. Shirazi, W. Drexler, C. K. F. Hitzenberger, R. A. Leitgeb, R. Ramlau and M. Pircher, In-vivo demonstration of AO-OCT with a 3-sided pyramid wavefront sensor (Conference Presentation). In Ophthalmic Technologies XXX, volume 11218, edited by F. Manns, A. Ho and P. G. Söderberg, International Society for Optics and Photonics, SPIE (2020)
5. R. Davies, J. Alves, R. Ramlau, R. Wagner, V. Hutterer, J. Niebsch et al., The MICADO first light imager for the ELT: overview, operation, simulation. In Proceedings of the SPIE Astronomical Telescopes and Instrumentation Conference, Vol. 10702 (Austin, Texas, June 2018): Ground-based and Airborne Instrumentation for Astronomy VII, edited by C. J. Evans, L. Simard and H. Takami, SPIE, 570–581 (2018)
6. S. Dolgov, D. Kalise and K. K. Kunisch, Tensor decomposition methods for high-dimensional Hamilton–Jacobi–Bellman equations. SIAM J. Sci. Comput.43, A1625–A1650 (2021)
7. A. Effland, E. Kobler, K. Kunisch and T. Pock, Variational networks: an optimal control approach to early stopping variational methods for image restoration. J. Math. Imaging Vision62, 396–416 (2020)
8. H. W. Engl and R. Ramlau. Regularization of inverse problems. In Encyclopedia of Applied and Computational Mathematics, edited by B. Engquist, Springer, Heidelberg (2015)
9. P. Grohs and L. Herrmann, Deep neural network approximation for high-dimensional parabolic Hamilton–Jacobi–Bellman equations. arXiv:2103.05744 (2021)
10. P. Grohs, F. Hornung, A. Jentzen and P. Von Wurstemberger. A proof that artificial neural networks overcome the curse of dimensionality in the numerical approximation of Black–Scholes partial differential equations. Memoirs of the AMS, to appear (2020)
11. V. Hutterer, R. Ramlau and I. Shatokhina, Real-time adaptive optics with pyramid wavefront sensors: part I. A theoretical analysis of the pyramid sensor model. Inverse Problems35, 045007 (2019)
12. J. A. Iglesias and G. Mercier, Influence of dimension on the convergence of level-sets in total variation regularization. ESAIM Control Optim. Calc. Var.26, Paper No. 52 (2020)
13. K. Kunisch and D. Walter, Semiglobal optimal feedback stabilization of autonomous systems via deep neural network approximation. ESAIM Control Optim. Calc. Var.27, Paper No. 16 (2021)
14. R. Ramlau and O. Scherzer (eds.), The Radon transform. The First 100 Years and Beyond. Radon Ser. Comput. Appl. Math. 22, De Gruyter, Berlin (2019)
15. M. Scherbela, R. Reisenhofer, L. Gerard, P. Marquetand and P. Grohs, Solving the electronic Schrödinger equation with weight-sharing deep neural networks for multiple nuclear geometries. arXiv:2105.08351 (2021)