A Diophantine equation concerning epimoric ratios

Preda Mihăilescu; Daniel Muzzulini

doi:10.4171/mag/84

In this paper, we solve an interesting Diophantine equation that is born from classical questions of music theory.

1 Introduction

This paper investigates a Diophantine equation derived from a principle of construction for musical harmonies and scales advocated in antiquity by Claudius Ptolemy (c. 85–160 AD), known also for his geocentric model of celestial motion. Ptolemy’s “Harmonics” was one of the main sources for Greek music theory in the Middle Ages and remained influential in the Renaissance up to the 17th century [⁠3⁠ A. Barker, Scientific method in Ptolemy’s “Harmonics”. Cambridge University Press, New Haven (2000) , ⁠4⁠ A. Barker, Mathematical beauty made audible: Musical aesthetics in Ptolemy’s “Harmonics”. Classical Philology 105, 403–420 (2010) , ⁠16⁠ J. Solomon, Ptolemy, “Harmonics”: Translation and commentary. Brill, Leiden (2000) ].

Retrospectively, the theory of proportions in the Pythagorean tradition can be considered a theory for rational numbers greater than one under multiplication⁠¹⁠We are aware that the antique ratios are not yet fully fledged rational numbers, i.e., classes of ordered pairs of integers. Whereas ratios were considered equivalent to their representations in lowest terms, the order of the terms of a ratio was not constitutive. The ratios $3 : 4$ and $4 : 3$ , for instance, represent the same relationship (the epitriti or sesquitertia) corresponding to the musical interval of the fourth (the diatessaron, see Figure ⁠1⁠) in the sense of a perceptual distance. For our purpose the restriction to rational numbers greater than 1 is sufficient and convenient.. In its application to musical harmonies and scales, adding musical intervals corresponds to the multiplication of rational numbers, and therefore piling equal intervals, i.e., multiplying a given interval by an integer, is equivalent with raising its ratio to the respective integer power⁠²⁠The term musical interval refers to logarithms of frequency ratios. Many quantifiable sensory phenomena and their physical counterparts are in a logarithmic or nearly logarithmic relationship, as loudness or brightness sensation with respect to the intensity of sound or light..

*Figure 1.* Arc diagram showing a complete graph with epimoric ratios. The nodes are labelled with numbers and note names, and the arcs with the Greek and Latin names of the related intervals. The six pairs of numbers *tonus* (whole tone), *diatessaron* (fourth), *diapente* (fifth), *diapason* (octave) form epimoric ratios. The diagram is remarkable because it represents equal intervals, i.e., logarithms of ratios, as equal semicircles, and not on a linear scale. It is a marginal note by Swiss music theorist Heinrich Loriti Glareanus (1488–1563) added to a manuscript copy from c. 1200 of the “Micrologus” by Guido of Arezzo (c. 991–992 until after 1033). ©
All rights reserved.

According to Ptolemy’s music-aesthetic premises, the multiple and the so-called epimoric ratios are the building blocks of musical harmonies and scales. Epimoric ratios (also called superparticular ratios) are positive rational numbers of the form $\frac{n + 1}{n}$ , whereas multiple ratios of the form $\frac{n}{1}$ are ordinary natural numbers. Since they can be written as the unit plus a unit fraction ( $1 + \frac{1}{n}$ ), epimoric ratios can be regarded as an elementary form of improper fractions accessible to perception guided by the intellect, see [⁠3⁠ A. Barker, Scientific method in Ptolemy’s “Harmonics”. Cambridge University Press, New Haven (2000) , pp. 60–62], [⁠4⁠ A. Barker, Mathematical beauty made audible: Musical aesthetics in Ptolemy’s “Harmonics”. Classical Philology 105, 403–420 (2010) ] and [⁠7⁠ P. Gozza, Number to sound: The musical way to the scientific revolution. The Western Ontario Series in Philosophy of Science 64, Springer, Dordrecht (2000) , pp. 191–200]. The role of epimoric ratios in music theory and pitch perception was repeatedly emphasized and problematized throughout the course of history – in the second half of the 16th century for instance, they were debated by Gioseffo Zarlino (1517–1590) and Vincenzo Galilei⁠³⁠The father of Galileo. (1520–1591) [⁠14⁠ B. V. Rivera, Theory ruled by practice: Zarlino’s reversal of the classical system of proportions. Indiana Theory Review 16, 145–160 (1995) , ⁠15⁠ F. Sargolini, La critica di Vincenzo Galilei al misticismo numerico di Gioseffo Zarlino. Nuncius 15, DOI 10.1163/182539100X00038 (2000) ]. On the other hand, epimoric ratios also played a crucial role in the development of novel calculation techniques: Simon Stevin (1548/49–1620) used various epimoric bases in his tables of compound interest, and Jost Bürgi (1552–1632) created a fine-grained and very accurate exponential table with more than 23,000 entries for the epimoric base $1 + \frac{1}{10 , 000}$ , see [⁠17⁠ S. Stevin, Tafelen van interest, midtgaders de constructie der selver … Christoffel Plantijn, Antwerpen (1582) ], [⁠18⁠ S. Stevin, The principal works of Simon Stevin. Vol. IIA: Mathematics. C. V. Swets & Zeitlinger, Amsterdam (1958) , p. 75] and [⁠11⁠ D. Muzzulini, The geometry of musical logarithms. Acta Musicologica 87, 193–216, DOI 10.5281/zenodo.5541790 (2015) , pp. 199–200, 209–210].

*Figure 2.* Triangular table used by Boethius to calculate finite geometric sequences of integers with the common epimoric factor $5/4$ . Only the first row requires repeated multiplication by $4$ . The numbers in any row can be found by adding neighbors from the previous one: $1 + 4 = 5, 4 + 16 = 20, 16 + 64 = 80, etc.$ The main diagonal direction holds the powers of $5$ , and the columns contain the geometric sequences in lowest terms. From the fourth column one can read that three major thirds $5/4$ are smaller than an octave because $(5/4) 3 (128/125) = 2$ . The method can be used for arbitrary epimoric ratios. There are examples for $3/2$ , $4/3$ , $5/4$ and $9/8$ in medieval Boethius manuscripts. ©
All rights reserved.

Archytas of Tarentum (c. 420–c. 350 BC) proved that the equation

(\frac{n + 1}{n})^{k} = \frac{s + 1}{s}

has no integer solutions in $n, s$ for integer exponents $k > 1$ (see [⁠2⁠ A. Barker, Ptolemy’s Pythagoreans, Archytas, and Plato’s conception of mathematics. Phronesis 39, 113–135 (1994) ]). Archytas’ reasoning was discussed by Boethius (c. 477–524 AD) [⁠9⁠ C. A. Huffman, Archytas of Tarentum: Pythagorean, philosopher and mathematician king. Cambridge University Press, Cambridge (2007) , pp. 451–470], who also quotes a more general result and its proof from the Euclidean “Sectio Canonis”⁠⁴⁠See [⁠1⁠ A. Barker, Greek musical writings: II Harmonic and acoustic theory. Cambridge University Press, Cambridge (1989) , p. 195]; the assignment of the “Sectio Canonis” to Euclid is insecure., stating that epimoric ratios can be decomposed in no way into products of two or more equal integer ratios – [⁠5⁠ Boethius, De institutione arithmetica libri duo: De institutione musica libri quinque. B. G. Teubner, Leipzig (1867) , Inst. Mus. IV.2, p. 303], [⁠6⁠ Boethius, Fundamentals of music. Yale University Press, New Haven (1989) , p. 118].

*Figure 3.* *Left*: Since twice the number on top 262,144 ( $= 8^{6}$ ) is less than 531,441 ( $= 9^{6}$ ), six epimoric tones ( $9/8$ ) are by a Pythagorean comma ( $531, 441/524, 288 = 3^{12} / 2^{19}$ ) greater than the octave, as the diagram by Jacobus Leodiensis (14th century) illustrates. *Right*: Twelve epimoric semitones of the ratio $18/17$ , however, are a little smaller than an octave, as Gioseffo Zarlino’s monochord calculations show. The epimoric ratio $18/17$ was proposed by Vincenzo Galilei as a substitute for the 12th root of two – it is the best epimoric approximation to the semitone of our modern piano tuning. The monochord string AB is divided at C in the middle, the horizontal system of lines $d, e, f, \dots, p$ indicate fret positions on the string, which is to be plucked between the frets and B (*estremo acuto*) to give the corresponding notes of this regular scale with a small non-epimoric gap between $p$ and C. ©
All rights reserved.

In other words, musical intervals of an epimoric ratio, such as the octave $(s = 1)$ or the fourth $(s = 3)$ , cannot be divided equally into smaller intervals of epimoric ratios, i.e., equal division results in “irrational ratios”⁠⁵⁠Irrationality had a precarious ontological status as being defined only ex negativo, and it was linked to incommensurable (geometric) quantities, see also [⁠12⁠ P. Pesic, Hearing the irrational: Music and the development of the modern concept of number. Isis 101, 501–530 (2010) ].. This fact makes it impossible to construct musical scales or scale segments with several equal intervals of epimoric ratios spanning for example a fourth or an octave. Our theorem, the main result of this paper, proves that a similar restriction holds for the partition of an epimoric ratio into a power of an epimoric ratio and a single epimoric cofactor: It shows that for positive integers $q, r, s$ and exponent $k > 2$ , equation (⁠1⁠) below has no solutions⁠⁶⁠The conjecture that (⁠1⁠) has no solutions was formulated by the second author, from the study of music theory and on the basis of his mathematical background. It was eventually settled in a joint effort of the two authors.. Introducing an epimoric cofactor, $\frac{r + 1}{r}$ , into the decomposition raises the upper bound $k$ for solvability only by $1$ .

2 The main theorem

We will prove the following theorem.

Theorem 1.

The Diophantine equation

(\frac{q + 1}{q})^{k} \cdot \frac{r + 1}{r} = \frac{s + 1}{s}, q, r, s \in N, k > 2,

has no integer solutions.

The following derivation holds for all $k \geq 2$ . The value $k = 2$ allows for an infinity of solutions; it will be considered in detail in a separate paper. By removing denominators, we obtain the following two equivalent formulations of (⁠1⁠):

(q + 1)^{k} \cdot (r + 1) s = q^{k} r (s + 1);

((q + 1)^{k} - q^{k}) (r + 1) s = q^{k} (rs + r - rs - s) = q^{k} (r - s) .

The last identity in (⁠3⁠) implies that $r - s > 0$ , so we can in particular divide by $r - s$ .

We define $δ = (q + 1)^{k} - q^{k}$ and note that

δ = k q^{k - 1} \cdot (1 + \frac{k - 1}{2} \frac{1}{q} + O (\frac{1}{q ^{2}})) < k q^{k - 1} \cdot (q (e^{1/ q} - 1)) .

In both equations (⁠2⁠) and (⁠3⁠), we encounter various pairs of factors of the type $(x, x + 1)$ for some $x \in N$ , for instance $s, s + 1$ in (⁠2⁠). These are coprime and in order to exploit this useful fact, we define a series of factors whose existence follows from such relations of coprimality. Namely, we set $A = (r + 1, r - s) = (r + 1, s + 1)$ and $B = (s, r - s) = (r, s)$ . We assume $A, B > 0$ and let the cofactors be $A C = s + 1$ and $B D = s$ for some $C, D \in N$ . Since $(q^{k}, (q + 1)^{k}) = 1$ , it follows that $q^{k} ∣ (r + 1) s$ and $δ ∣ r - s$ . By combining the last relations of divisibility with the definitions of $A$ and $B$ , we get

(r + 1) s = A B \cdot q^{k}, r - s = A B \cdot δ,

\frac{q ^{k}}{δ} = s \cdot (1 + \frac{s + 1}{r - s}) > s .

Using the upper bound on $δ$ in (⁠4⁠), we obtain the following estimates for $s$ .

Lemma 1. Assuming that (⁠1⁠) has non-trivial integral solutions, $s$ obeys the bounds

\frac{q}{k μ} < s < \frac{q ^{k}}{δ} < \frac{q}{k}, with μ = q (e^{1/ q} - 1) \cdot (1 + \frac{s + 1}{r - s}) .

In particular, $q > k$ .

Proof. The upper bound for $s$ follows from (⁠5⁠); the lower bound follows from the same identity, in conjunction with the upper bound in (⁠4⁠). Since $s \geq 1$ , we obtain our first lower bound for $q$ , namely $\frac{q}{k} > s \geq 1$ , hence $q > k$ . ∎

Our next task is to derive from the above and some additional bounds, a tight interval which must contain $s$ ; en route we also obtain sharper lower bounds on $q$ .

Lemma 2. Under the same assumption as above, we let

Q = (\frac{q}{k} + 1) \cdot \frac{q}{k} and U : - \frac{q ^{k} - Q}{δ}, V : - \frac{q ^{k} - 1}{δ} .

Then

s \in I : - (U, V) .

Moreover, $q > (k - 1)^{k + 1}$ and there is at most one integer $σ \in I \cap N$ . In particular, if (⁠1⁠) has a solution, then $s = σ$ .

Proof. We have

r = s + r - s = A B \cdot (\frac{q ^{k}}{r + 1} + δ) .

Now, $(B, r + 1) = 1$ and $A ∣ (r + 1)$ , so the previous becomes

r = A B δ + B \frac{q ^{k}}{( r + 1 ) / A} .

Since $(B, r + 1) = 1$ , it follows that $(r + 1) ∣ A q^{k}$ , and in (⁠5⁠), we find

B \cdot (\frac{A q ^{k}}{r + 1}) = s .

Since $(A, s) = 1$ , we get

(\frac{s}{B}) = D ∣ q^{k},

hence $s = B D ∣ r q^{k}$ . Reinserted in (⁠5⁠) with the definition $r : - r^{'} \cdot B$ , this leads to

r + 1 = A \frac{q ^{k}}{D} and r^{'} - D = A \cdot δ .

So

r = A (\frac{q ^{k}}{D}) - 1 and r^{'} = \frac{r}{B} = A δ + D,

thus

s = \frac{A q ^{k} - D}{A δ + D} \in N;

consequently,

s \cdot δ + \frac{sD}{A} = q^{k} - \frac{D}{A},

C D = D \frac{s + 1}{A} = q^{k} - sδ = q^{k} (s + 1) - s (q + 1)^{k} .

Since $C D \leq s (s + 1) < Q$ , we conclude that

\frac{q ^{k} - 1}{δ} \geq s = \frac{q ^{k} - C D}{δ} > \frac{k ^{2} q ^{k} - q ( q + k )}{k ^{2} (( q + 1 ) ^{k} - q ^{k} )} .

Statement (⁠7⁠) follows from these inequalities, by inserting the definitions of $U$ and $V$ . The length of the interval $I$ is $ℓ = \frac{Q - 1}{δ}$ ; the improved lower bound on $q$ will show that $ℓ < \frac{1}{2}$ for $k \geq 3$ , and thus the interval $I$ contains at most one integer, which confirms the statement on $σ$ .

Now $D ∣ q^{k}$ , so

B = \frac{\frac{q ^{k}}{D} - C}{( q + 1 ) ^{k} - q ^{k}} .

Since $D \leq s < \frac{q}{k}$ , we also have $\frac{q ^{k}}{D} > k q^{k - 1}$ . This will lead to the bound for $q$ . Assume first that $\frac{q ^{k}}{D} \equiv 0 mod q$ . Then $B + C \equiv 0 mod q$ . But $B + C \leq 2 s + 1 < 2 \frac{q}{k} + 1 < q$ for $q > k > 2$ , so we obtain a contradiction to $B + C \geq 0$ , and thus $B = C = 0$ , which is absurd.

It remains to treat the case $\frac{q ^{k}}{D} \neq \equiv 0 mod q$ . We decompose $D = a d^{k}$ , so that all primes $p$ that divide $a$ are either coprime to $q$ , or occur in $a$ with a power less than $k$ , while $d ∣ (q, D)$ . Then $\frac{q ^{k}}{D} = a (\frac{q}{d})^{k} \equiv 0 mod \frac{q}{d}$ and (⁠6⁠) implies a fortiori that $B k d^{k} < q$ holds along with $B + C \equiv 0 mod \frac{q}{d}$ . Since $B, C > 0$ , we have

\frac{q}{k} > C \geq \frac{q - B d}{d} ⟹ d q > k q - B k d > k q - \frac{q}{d ^{k - 1}},

and thus $d - (k - \frac{1}{d ^{k - 1}}) > 0$ and a fortiori $d \geq k - 1$ . In particular, $q$ must be large, namely

q > B (k - 1)^{k + 1} \geq (k - 1)^{k + 1},

as claimed. Using this bound, a straightforward verification shows that $ℓ < \frac{1}{2}$ , and this completes the proof of Lemma ⁠2⁠. ∎

We finally use the bound (⁠10⁠) and sharper estimates for $δ$ to complete the proof of Theorem 1. If $I \cap N = \emptyset$ , then there are no solutions, and we are done. Otherwise, we let $σ$ be the unique integer in the interval $I$ . Since $s \in I$ is also an integer, it follows that $s = σ$ .

Proof of Theorem ⁠1⁠. We determine $σ$ in terms of $\frac{q}{k}$ . We have

δ : - (q + 1)^{k} - q^{k} = q^{k - 2} (q k + (2 k) + \frac{1}{q} (3 k) + ρ),

with

∣ ρ ∣ \leq ⎩ ⎨ ⎧ 0 \frac{k ^{4}}{4 ! q ^{2}} < \frac{1}{20 q} for k = 3, for k > 3, using q > (k - 1)^{k + 1} .

Consequently,

δ σ = q^{k - 2} σ (q k + (2 k) + \frac{1}{q} (3 k) + ρ) = q^{k} - C D,

σ \cdot (q k + (2 k)) + \frac{σ}{q} (3 k) = q^{2} - ρ_{1},

where

∣ ρ_{1} ∣ = \frac{C D}{q ^{k - 2}} - σ ρ .

Since $σ < \frac{q}{k}$ , there is a number $e$ of the form $e = {\frac{q}{k}} + n$ , with $n \in Z_{\geq 0}$ and ${\frac{q}{k}}$ denoting the fractional part of $\frac{q}{k}$ , such that

σ = \frac{q}{k} - e = [\frac{q}{k}] - n, e k = q - kσ .

We claim that $n = 0$ . The definition of $U$ implies that

nk = q - [q - kσ] \leq \frac{k q ^{k} ( 1 + \frac{k - 1}{2 q} + O ( \frac{1}{q ^{2}} ) ) - k q ^{k} + \frac{q ^{2}}{k}}{δ} \leq \frac{( 2 k ) q ^{k - 1} + \frac{q ^{2}}{k} + O ( q ^{k - 2} )}{k q ^{k - 1}} < ⌈ \frac{k - 1}{2} ⌉ \leq \frac{k + 1}{2} .

Since $n$ is an integer and $0 \leq n < \frac{k + 1}{2 k}$ , it follows that $n = 0$ and $0 < e k < k$ , as claimed.

Thus, $σ = \frac{q}{k} - e = [\frac{q}{k}]$ . Inserting this value of $σ$ in (⁠8⁠) yields

q^{2} - e q k + \frac{k - 1}{2} q - \frac{e k ( k - 1 )}{2} + \frac{( k - 1 ) ( k - 2 )}{6} - (3 k) \frac{e}{q} = q^{2} - ρ_{1},

hence

q \cdot (\frac{k - 1}{2} - e k) = R^{'} : - - \frac{e k ( k - 1 )}{2} + \frac{( k - 1 ) ( k - 2 )}{6} + ρ_{2},

with

∣ ρ_{2} ∣ = ρ_{1} - (3 k) \frac{e}{q} \leq ∣ ρ_{1} ∣ + \frac{k ( k - 1 ) ( k - 2 )}{6 q} .

We have seen that $e k \in N$ , so if the left-hand side of (⁠11⁠) does not vanish, then its cofactor is an integer or a half-integer; if it does not vanish, its absolute value will exceed $\frac{q}{2}$ . We denoted the right-hand side of (⁠11⁠) by $R^{'}$ , so

∣ R^{'} ∣ \leq ∣ R ∣ + \frac{k - 1}{2} \cdot \frac{k - 2}{3} - e k < \frac{k ( k - 1 )}{3} + ∣ R ∣ .

For the right-hand side, small values of $k$ allow for larger values of $ρ_{2}$ , so we first assume $k \geq 4$ . In this case

∣ ρ_{2} ∣ \leq R : - \frac{Q}{q ^{k - 2}} + \frac{σ}{20 q} + \frac{k ( k - 1 ) ( k - 2 )}{6 ( k - 1 ) ^{5}} < \frac{2}{( k - 1 ) k} .

Now $∣ R ∣ < (\frac{1}{k ^{2}} + \frac{1}{q k} + \frac{1}{20 k}) + \frac{6}{( k - 1 ) ^{k - 2}} < \frac{1}{k} \cdot (\frac{2}{k} + \frac{1}{20})$ and inserting this in the bound for $R^{'}$ , we see that $∣ R^{'} ∣ < (k - 1)^{2} < \frac{q}{2}$ . Since the left-hand side is at least $\frac{q}{2}$ in absolute value, if it does not vanish, we conclude that the two sides must vanish simultaneously. Thus, $e = \frac{k - 1}{2 k}$ and the right-hand side is $\frac{k ^{2} - 1}{12} - ρ_{2}$ . Since $∣ ρ_{2} ∣ < 1$ and $\frac{k ^{2} - 1}{12} > 1$ for $k > 3$ , the last expression cannot vanish for $k > 3$ , so there are no solutions in this case.

The case $k = 3$ is more delicate; recall that in this case $ρ = 0$ and thus $ρ_{2} = \frac{C D - e}{q}$ . The best bound for the error term is now $0 < ∣ ρ_{2} ∣ < \frac{q}{9}$ , so in (⁠11⁠)

q = 3 e (q - 1) + \frac{1}{3} + ρ_{2} = 3 e (q - 1) + \frac{1}{3} + \frac{C D - e}{q} .

We generate a contradiction by a case-by-case examination. We know that $3 e < k = 3$ , so $3 e \in {0, 1, 2}$ . The cases $3 e = 0$ and $3 e = 2$ are easily seen to be impossible. In the first case, the right-hand side is too small, while in the second case it is too large, compared to $q$ , as one verifies from the definitions.

If $3 e = 1$ , we obtain

q = q - 1 + \frac{1}{3} + \frac{C D - \frac{1}{3}}{q} ⟹ \frac{q + 3 C D - 1}{3 q} = 1,

thus $C D = \frac{2 q + 1}{3} = \frac{2 q + 1}{k}$ . We have seen above that $D ∣ q^{k}$ , while $3 C D = 2 q + 1$ implies $D ∣ (2 q + 1, q^{3})$ , and thus $D = 1$ . But then $C = C D = \frac{2 q + 1}{3} > \frac{q}{3} + 1$ , contradicting the upper bound $C \leq s + 1 < \frac{q}{k} + 1$ established above. We conclude that there are no solutions for $k = 3$ either, and this completes the proof. ∎

3 Remarks and comments

Here we provide some historical details that place our result in its musical context. For additional reading we recommend the excellent modern introduction to superparticular ratios⁠⁷⁠This is an other expression for epimoric ratios. by Halsey and Hewitt [⁠8⁠ G. D. Halsey and E. Hewitt, More on the superparticular ratios in music. Amer. Math. Monthly 79, 1096–1100 (1972) ].

3.1 Music theory

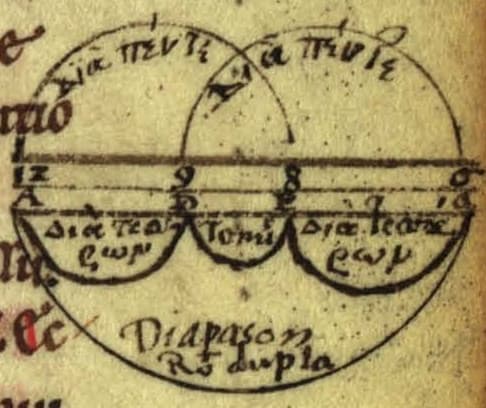
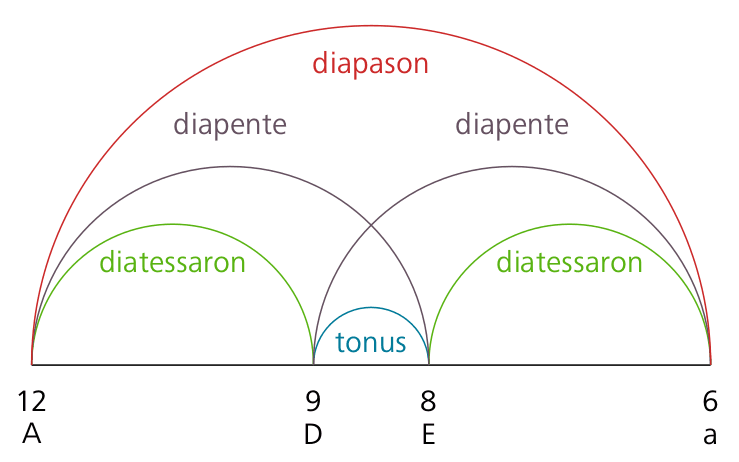
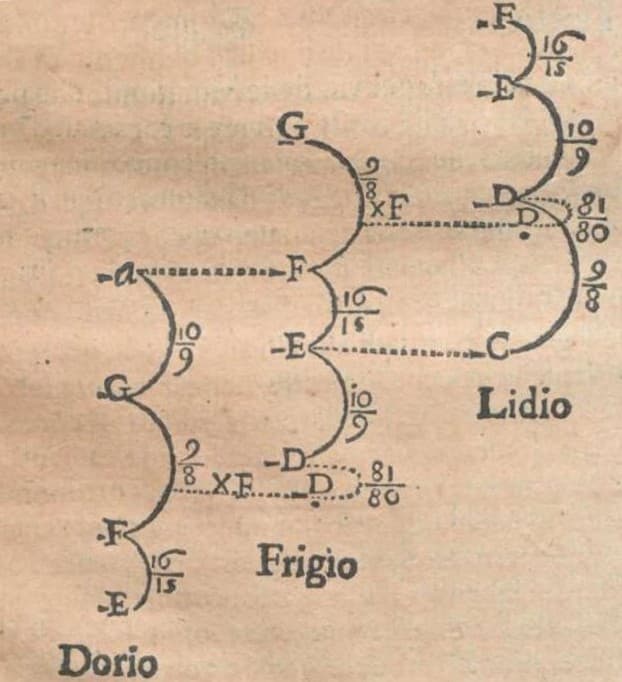
In order to briefly elucidate the musical context of the theorem, we give some examples. Historically, partitions of ratios are frequently written as ordered multi-term proportions within arc diagrams. Arrangements as proportions in lowest terms corresponding to the left-hand side of the following equalities are given in brackets.

*Figure 4.* *Left*: Ptolemy’s diatonic scale according to Gioseffo Zarlino. The baseline holds the proportion $90 : 96 : 108 : 120 : 135 : 144 : 160 : 180$ (from right to left) with three major tones ( $9/8 = Sesqui 8$ ), two minor tones ( $10/9 = Sesqui 9$ ) and two (major) semitones ( $16/15 = Sesqui 15$ ). The fourth (*diatessaron*) of the Ptolemaic tetrachord highlighted at the bottom consist of a semitone (16/15), a major tone (9/8) and a minor tone (10/9). Only intervals of epimoric ratios are labelled in this almost complete graph with eight nodes. *Right*: Greek tetrachords in the 17th century. Doni’s system with three “epimoric tetrachords” E–A (dorian), D–G (phrygian) and C–F (lydian) uses two varieties of whole tone steps (9/8 and 10/9), semitones E–F (16/15) as well as two pitches for D differing by a syntonic comma (81/80) resulting in a fine grained system of pitches [⁠10⁠, pp. 62–69]. ©
All rights reserved.

With $k = 1$ , the octave (2/1) can be divided into a fifth (3/2) and a fourth (4/3):

\frac{3}{2} \cdot \frac{4}{3} = \frac{2}{1} (2 : 3 : 4)

and with $k = 2$ , into two fourths and a whole tone (9/8), see Figure ⁠1⁠:

(\frac{4}{3})^{2} \cdot \frac{9}{8} = \frac{2}{1} (6 : 8 : 9 : 12) .

Likewise, the fifth (3/2) can be partitioned with two minor thirds (6/5) and a chromatic semitone (25/24):

(\frac{6}{5})^{2} \cdot \frac{25}{24} = \frac{3}{2} (20 : 24 : 25 : 30) .

However, no epimoric musical interval can be divided into four epimoric smaller intervals, of which three are equal $(k = 3)$ . For example, the Pythagorean division of the fifth into three whole tones and a non-epimoric remainder,

(\frac{9}{8})^{3} \cdot \frac{256}{243} = \frac{3}{2} (192 : 216 : 243 : 256 : 288),

or the division of the octave into three major thirds (5/4) and a diesis (128/125),

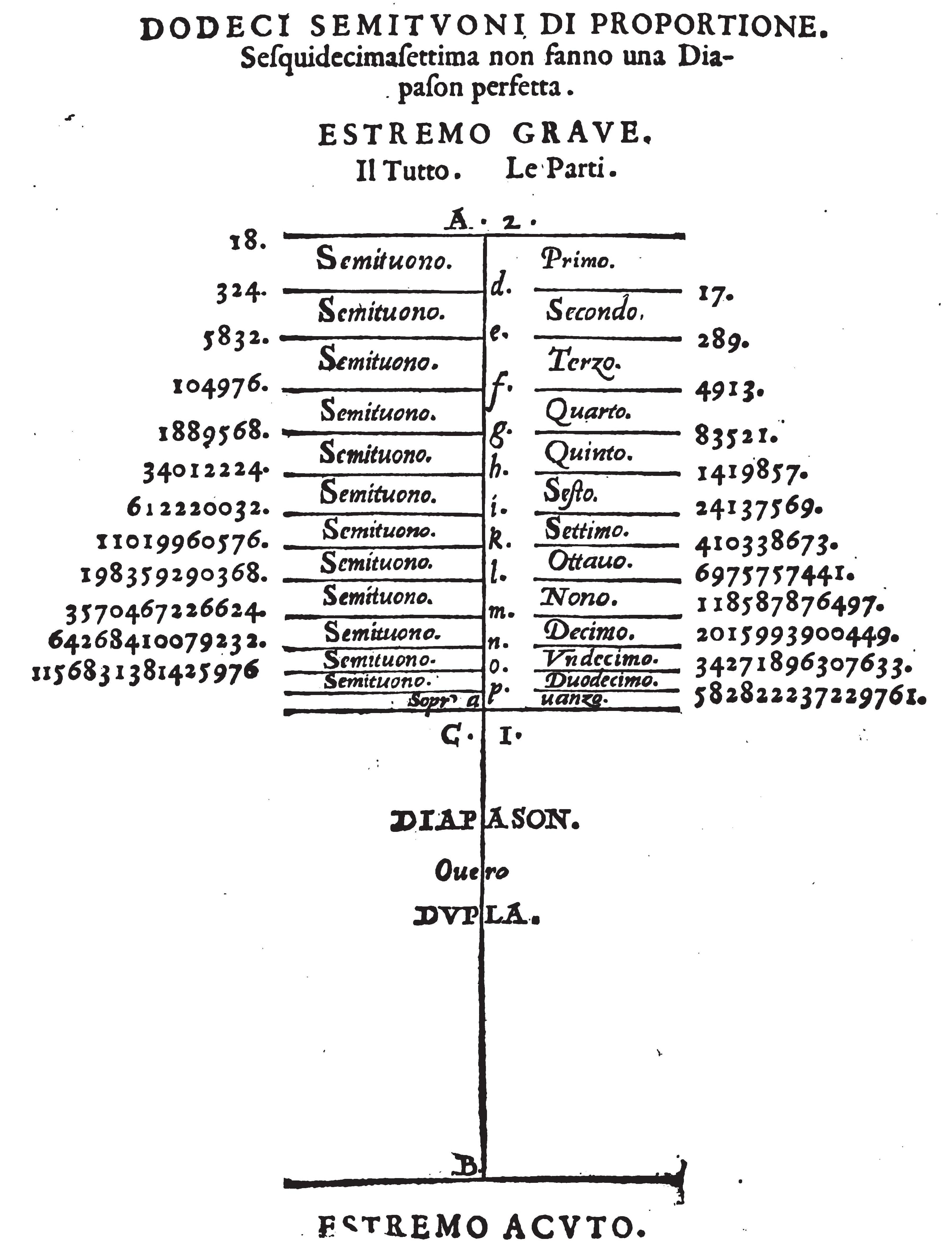
(\frac{5}{4})^{3} \cdot \frac{128}{125} = \frac{2}{1} (64 : 80 : 100 : 125 : 128),

are prototypical: Whatever cubed epimoric ratio is chosen, the cofactors to 3/2 and 2/1 are never epimoric. The latter example illustrates that the just intonation major third (5/4) is an approximation to the problem of doubling the cube, whereas the irrational major thirds of the present-day equal division of the octave is a true solution beyond antique ratio theory⁠⁸⁠Illustrations for $k = 6$ and $k = 12$ , where $s = 1$ (the octave), from sources of the 14th and 16th century are given in Figure ⁠3⁠..

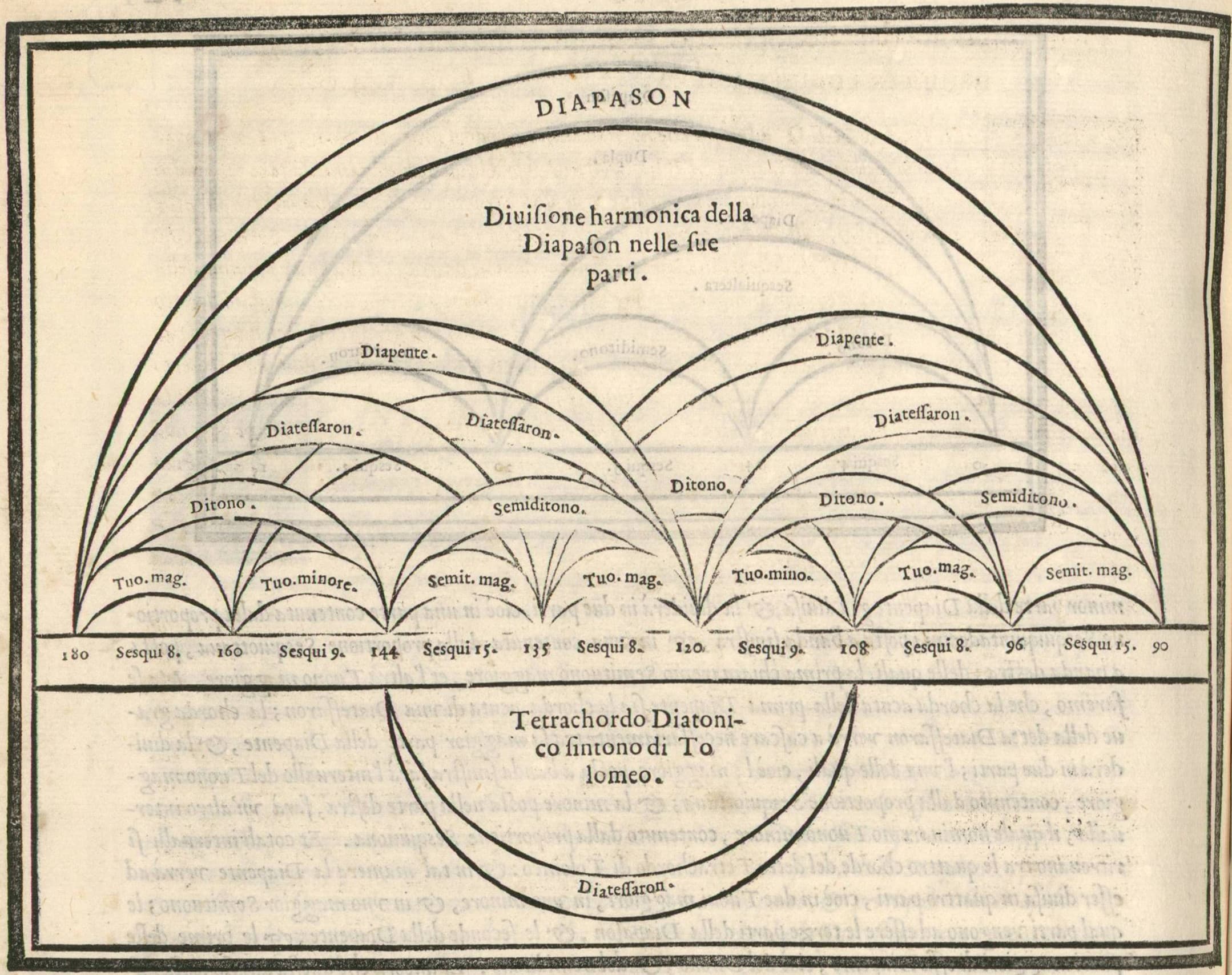
Ptolemy’s tetrachords (divisions of the fourth) involved three different epimoric ratios, as in

\frac{9}{8} \cdot \frac{10}{9} \cdot \frac{16}{15} = \frac{4}{3} .

Combining this with (⁠12⁠) results in the octave division

(\frac{9}{8})^{3} \cdot (\frac{10}{9})^{2} \cdot (\frac{16}{15})^{2} = \frac{2}{1},

where 9/8 and 10/9 define two varieties of whole tones and 16/15 a semitone larger than the Pythagorean 256/243. This partition can be used to define the diatonic scale in just intonation, see Figure ⁠4⁠ (left). The Pythagorean example (⁠13⁠) which fails to be made up solely of epimorics, is an indication for the origin of our problem (⁠1⁠).

3.2 Diophantine equations

Music Theory stood more than once at the origin of fascinating Diophantine equations. For instance, the reputed Catalan equation⁠⁹⁠Catalan proposed this equation in a French journal in 1841 and it appeared in Crelle’s Journal as a note to the Editor, in 1844. $x^{u} - y^{v} = 1$ , stating that $8$ and $9$ are the only successive non-trivial powers of integers, generalizes the original question about $3^{x} - 2^{y} = 1$ considered by Philippe de Vitry (1291–1361) in relation with harmonic numbers and Platonic music theory, thus a Diophantine equation with actual connection to music. Levi ben Gershon (1288–1344) had proved that this particular equation does not have other solutions than $9 - 8 = 1$ , and this already in the 13th century. Leonhard Euler (1717–1783) switched exponents and bases in the musical equation, and finally Catalan (1814–1894) allowed both bases and exponents to vary: both latter variations had left the common field of music and mathematics, and Diophantine equations were investigated for their pure mathematical interest.

The present equation (⁠1⁠) still has a lively connection to music theory. Were this of no more concern, one could imagine generalizations of (⁠1⁠) such as

(\frac{q + 1}{q})^{k} \cdot (\frac{r + 1}{r})^{l} = (\frac{s + 1}{s})^{m}, q, r, s \in N, k, l, m > 2,

or, defining

ℓ (q, m) = 1 + \frac{1}{n} + \frac{1}{n + 1} + \dots + \frac{1}{n + m},

one could look at

ℓ (q, n)^{k} \cdot ℓ (r, n)^{l} = ℓ (s, n)^{m}, q, r, s \in N, k, l, m, n > 2,

All this recalls the falling powers

x^{\underline{n}} = x (x - 1) \dots (x - n + 1),

dear to Isaac Newton (1643–1727), and one finds a variant of Fermat’s Last Theorem, that cannot be found among the dozen of variants mentioned in Ribenboim’s 13 Lectures [⁠13⁠ P. Ribenboim, 13 lectures on Fermat’s last theorem. Springer, New York (1979) ], probably the most adequate source for verifying if a variant of Fermat’s Equation has already received attention. This one apparently did not:

x^{\underline{p}} + y^{\underline{p}} = z^{\underline{p}}, (x, y, z) = 1 and x, y, z > n + 1.

We stop here and invite the reader to imagine his own favorite generalization, leaving it to the future to decide whether some of these variations will capture the attention of a larger number of mathematicians, professional or not.

Image sources

Guido of Arezzo (c. 1200), Micrologus, Ms. 8 Cod. Ms. 375 (Cim 13), fol. 53r. Source: München, Universitätsbibliothek
A. M. S. Boethius (early 10th c.), De institutione arithmetica., fol. 4v. Source: Medeltidshandskrift 1 (Mh 1), Lund University Library
Jacobus (Leodiensis) (15th c.), Speculum musicae, Ms. Latin 7207, Vol. III, Cap LXXXV, fol. 46r. Source: gallica.bnf.fr/Bibliothèque nationale de France
G. Zarlino (1588), Sopplimenti musicali, Venetia: Francesco de Franceschi, Sanese, Lib IV, p. 205, https://s9.imslp.org/files/imglnks/usimg/d/d1/IMSLP129044-PMLP252086-terzo_volume.pdf (accessed February 21, 2022)
G. Zarlino (1562), Le istitutioni harmoniche, Venice, Italy, p. 122. https://digital.library.unt.edu/ark:/67531/metadc25955/ (accessed February 21, 2022), University of North Texas Libraries, UNT Digital Library, https://digital.library.unt.edu; crediting UNT Music Library
G. B. Doni (1635), Compendio del Trattato de’ Generi e de’ Modi della Musica, Roma, p. 41. Source: Mus.th. 7234, Bayerische Staatsbibliothek München

Preda Mihăilescu studied mathematics and computer science in Zürich, receiving his PhD from ETH Zürich. He was active during 15 years in the industry, as a numerical analyst and cryptography specialist. In 2002, he proved Catalan’s Conjecture. This number theoretical conjecture, formulated by the French mathematician E. C. Catalan in 1844, had stood unresolved for over a century. The result is known as Mihăilescu’s Theorem. He is currently a professor at the Institute of Mathematics of the University of Göttingen. preda@uni-math.gwdg.de Daniel Muzzulini studied mathematics, musicology, physics and philosophy at Zurich University, where he received his PhD with “Genealogie der Klangfarbe” (Peter Lang 2006). He had been assistant at ETH Zürich and research associate at Zurich University, and after studying informatics at the University of Applied Sciences (now FHNW) in Basel, he worked as a software developer until 2002. Afterwards, he was a teacher of mathematics and informatics at Alpenquai College in Lucerne until 2019. Since 2015 he has been the manager of the project “Sound Colour Space – A Virtual Museum” at Zurich University of the Arts (ZHdK). His main topics of research are the history of (mathematical approaches to) music theory and perception psychology as well as the history and theory of scientific diagrams. daniel.muzzulini@zhdk.ch

¹
We are aware that the antique ratios are not yet fully fledged rational numbers, i.e., classes of ordered pairs of integers. Whereas ratios were considered equivalent to their representations in lowest terms, the order of the terms of a ratio was not constitutive. The ratios $3 : 4$ and $4 : 3$ , for instance, represent the same relationship (the epitriti or sesquitertia) corresponding to the musical interval of the fourth (the diatessaron, see Figure ⁠1⁠) in the sense of a perceptual distance. For our purpose the restriction to rational numbers greater than 1 is sufficient and convenient.
²
The term musical interval refers to logarithms of frequency ratios. Many quantifiable sensory phenomena and their physical counterparts are in a logarithmic or nearly logarithmic relationship, as loudness or brightness sensation with respect to the intensity of sound or light.
³
The father of Galileo.
⁴
See [⁠1⁠ A. Barker, Greek musical writings: II Harmonic and acoustic theory. Cambridge University Press, Cambridge (1989) , p. 195]; the assignment of the “Sectio Canonis” to Euclid is insecure.
⁵
Irrationality had a precarious ontological status as being defined only ex negativo, and it was linked to incommensurable (geometric) quantities, see also [⁠12⁠ P. Pesic, Hearing the irrational: Music and the development of the modern concept of number. Isis 101, 501–530 (2010) ].
⁶
The conjecture that (⁠1⁠) has no solutions was formulated by the second author, from the study of music theory and on the basis of his mathematical background. It was eventually settled in a joint effort of the two authors.
⁷
This is an other expression for epimoric ratios.
⁸
Illustrations for $k = 6$ and $k = 12$ , where $s = 1$ (the octave), from sources of the 14th and 16th century are given in Figure ⁠3⁠.
⁹
Catalan proposed this equation in a French journal in 1841 and it appeared in Crelle’s Journal as a note to the Editor, in 1844.

References

A. Barker, Greek musical writings: II Harmonic and acoustic theory. Cambridge University Press, Cambridge (1989)
A. Barker, Ptolemy’s Pythagoreans, Archytas, and Plato’s conception of mathematics. Phronesis 39, 113–135 (1994)
A. Barker, Scientific method in Ptolemy’s “Harmonics”. Cambridge University Press, New Haven (2000)
A. Barker, Mathematical beauty made audible: Musical aesthetics in Ptolemy’s “Harmonics”. Classical Philology 105, 403–420 (2010)
Boethius, De institutione arithmetica libri duo: De institutione musica libri quinque. B. G. Teubner, Leipzig (1867)
Boethius, Fundamentals of music. Yale University Press, New Haven (1989)
P. Gozza, Number to sound: The musical way to the scientific revolution. The Western Ontario Series in Philosophy of Science 64, Springer, Dordrecht (2000)
G. D. Halsey and E. Hewitt, More on the superparticular ratios in music. Amer. Math. Monthly 79, 1096–1100 (1972)
C. A. Huffman, Archytas of Tarentum: Pythagorean, philosopher and mathematician king. Cambridge University Press, Cambridge (2007)
M. Kirnbauer, Vieltönige Musik – Spielarten chromatischer und enharmonischer Musik in Rom in der ersten Häfte des 17. Jahrhunderts. Schola Cantorum Basiliensis Scripta 3, Schwabe, Basel (2013)
D. Muzzulini, The geometry of musical logarithms. Acta Musicologica 87, 193–216, DOI 10.5281/zenodo.5541790 (2015)
P. Pesic, Hearing the irrational: Music and the development of the modern concept of number. Isis 101, 501–530 (2010)
P. Ribenboim, 13 lectures on Fermat’s last theorem. Springer, New York (1979)
B. V. Rivera, Theory ruled by practice: Zarlino’s reversal of the classical system of proportions. Indiana Theory Review 16, 145–160 (1995)
F. Sargolini, La critica di Vincenzo Galilei al misticismo numerico di Gioseffo Zarlino. Nuncius 15, DOI 10.1163/182539100X00038 (2000)
J. Solomon, Ptolemy, “Harmonics”: Translation and commentary. Brill, Leiden (2000)
S. Stevin, Tafelen van interest, midtgaders de constructie der selver … Christoffel Plantijn, Antwerpen (1582)
S. Stevin, The principal works of Simon Stevin. Vol. IIA: Mathematics. C. V. Swets & Zeitlinger, Amsterdam (1958)

Cite this article

Preda Mihăilescu, Daniel Muzzulini, A Diophantine equation concerning epimoric ratios. Eur. Math. Soc. Mag. 124 (2022), pp. 16–22

DOI 10.4171/MAG/84

🅭🅯

This open access article is published by EMS Press under a CC BY 4.0 license, with the exception of logos and branding of the European Mathematical Society and EMS Press, and where otherwise noted.

Back to Issue 124

[bib-bib1] A. Barker, Greek musical writings: II Harmonic and acoustic theory. Cambridge University Press, Cambridge (1989)

[bib-bib2] A. Barker, Ptolemy’s Pythagoreans, Archytas, and Plato’s conception of mathematics. Phronesis 39, 113–135 (1994)

[bib-bib3] A. Barker, Scientific method in Ptolemy’s “Harmonics”. Cambridge University Press, New Haven (2000)

[bib-bib4] A. Barker, Mathematical beauty made audible: Musical aesthetics in Ptolemy’s “Harmonics”. Classical Philology 105, 403–420 (2010)

[bib-bib5] Boethius, De institutione arithmetica libri duo: De institutione musica libri quinque. B. G. Teubner, Leipzig (1867)

[bib-bib6] Boethius, Fundamentals of music. Yale University Press, New Haven (1989)

[bib-bib7] P. Gozza, Number to sound: The musical way to the scientific revolution. The Western Ontario Series in Philosophy of Science 64, Springer, Dordrecht (2000)

[bib-bib8] G. D. Halsey and E. Hewitt, More on the superparticular ratios in music. Amer. Math. Monthly 79, 1096–1100 (1972)

[bib-bib9] C. A. Huffman, Archytas of Tarentum: Pythagorean, philosopher and mathematician king. Cambridge University Press, Cambridge (2007)

[bib-bib10] M. Kirnbauer, Vieltönige Musik – Spielarten chromatischer und enharmonischer Musik in Rom in der ersten Häfte des 17. Jahrhunderts. Schola Cantorum Basiliensis Scripta 3, Schwabe, Basel (2013)

[bib-bib11] D. Muzzulini, The geometry of musical logarithms. Acta Musicologica 87, 193–216, DOI 10.5281/zenodo.5541790 (2015)

[bib-bib12] P. Pesic, Hearing the irrational: Music and the development of the modern concept of number. Isis 101, 501–530 (2010)

[bib-bib13] P. Ribenboim, 13 lectures on Fermat’s last theorem. Springer, New York (1979)

[bib-bib14] B. V. Rivera, Theory ruled by practice: Zarlino’s reversal of the classical system of proportions. Indiana Theory Review 16, 145–160 (1995)

[bib-bib15] F. Sargolini, La critica di Vincenzo Galilei al misticismo numerico di Gioseffo Zarlino. Nuncius 15, DOI 10.1163/182539100X00038 (2000)

[bib-bib16] J. Solomon, Ptolemy, “Harmonics”: Translation and commentary. Brill, Leiden (2000)

[bib-bib17] S. Stevin, Tafelen van interest, midtgaders de constructie der selver … Christoffel Plantijn, Antwerpen (1582)

[bib-bib18] S. Stevin, The principal works of Simon Stevin. Vol. IIA: Mathematics. C. V. Swets & Zeitlinger, Amsterdam (1958)