ERME column

Regularly presented by Jason Cooper and Frode Rønning. In this issue, with a contribution by Anna Baccaglini-Frank, Carla Finesilver and Michal Tabach

Representations of mathematical concepts constitute an “integral part of the doing of mathematics” [⁠16⁠ N. C. Presmeg, Preface, In Representations and Mathematics Visualization, edited by F. Hitt, North American Chapter of the International Group for the Psychology of Mathematics Education, ix–xvi (2002) ] and, therefore, they are also an integral part of teaching and learning mathematics. Indeed, the theme of representation has for some time been a crucial topic in research in mathematics education – for instance, in PME groups (Psychology in Mathematics Education), and in special issues of the prestigious journals Educational Studies in Mathematics and ZDM Mathematics Education. The authors of this paper are currently co-leaders of the Thematic Working Group “Representations in Mathematics Teaching and Learning” of the 12th Congress of the European Society for Research in Mathematics Education (CERME12), and have been involved in the discussions of this working group ever since it was founded at CERME10 in 2017 [⁠17⁠ E. Robotti, A. Baccaglini-Frank, G. Sensevy and T. Fritzlar, TWG24: representations in mathematics teaching and learning. Introduction to the papers of TWG24. In Proceedings of CERME 10 (Dublin, 2017), hal-01950557 (2017) ]. The working group has continued its discussions over the years (e.g., [⁠2⁠ A. Baccaglini-Frank, C. Finesilver, S. Okumus and M. Tabach, Introduction to the work of TWG24: representations in mathematics teaching and learning. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (Utrecht, 2019), Utrecht, Netherlands, hal-02394695 (2019) ]) focusing on many pedagogical and theoretical aspects of mathematical representations. Some recurring themes in the discussions have been around the effective uses of different types of representation, imagery and visualization in mathematical problem solving, and how teachers can help learners to make connections between different representations of the same mathematical object.

Another recurring theme in many of these discussions is the advocacy of working with different forms of representation, and the valuing of non-standard forms. Group discussions have pointed to pressures that exist across many educational contexts for teachers to privilege particular standardized forms of representation over alternatives, in order to push students to acquire as swiftly as possible selected so-called “efficient” ways to produce answers [⁠7⁠ C. Finesilver, Low-attaining students’ representational strategies: tasks, time, efficiency, and economy. Oxford Review of Education 43, 482–501 (2017) ]. Since these pressures may prematurely curtail students’ creativity and intuitive approaches when engaging in problem solving [⁠4⁠ E. Deliyianni, A. Monoyiou, I. Elia, C. Georgiou and E. Zannettou, Pupils’ visual representations in standard and problematic problem solving in mathematics: their role in the breach of the didactical contract. European Early Childhood Education Research Journal 17, 95–110 (2009) ], discussions in our working group have focused on how to support teachers’ use of ​​more diverse representational forms and formats that enable wider inclusivity, providing all learners with opportunities to engage more meaningfully with mathematical activity and knowledge.

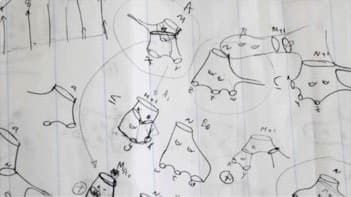
In support of this position we believe it is pertinent that creative mathematical thinking needs incubation time, and that it is very frequently supported by non-standard representations, developed as personal cognitive tools to implement or demonstrate particular objects or reasoning processes. For example, Maryam Mirzakhani, winner of the 2014 Fields Medal, was well known to “doodle” as a central part of her mathematical research process, repeatedly drawing and re-drawing figures (for example, those reproduced in Figure ⁠1⁠) on large sheets of paper spread out on the floor.

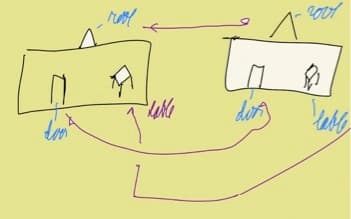
A second example is shown in the drawing from a brief comic book by Saharon Shelah, designed for a presentation of a recent result; the sketch in Figure ⁠2⁠ illustrates the notion of isomorphism.

As mentioned above, another recurring theme from our CERME group concerns the theoretical foundations and languages through which representations are thought about, viewed, designed and discussed. We focus on this theme in the rest of this contribution, to explain the significance for mathematics education of having different ways of “talking about” representations. This is an ongoing process: we are still developing appropriate concepts and vocabulary for researching certain kinds of representations, for example those that have a dynamic and interactive nature, or that are multimodal/multimedia, or co-created through collaborative activity. Such representations have become more frequently seen with the advent of digital technology in educational contexts, and because of educators’ increasing attention to fostering meaningful mathematical experiences in a variety of physical and digital contexts. More specifically, in this contribution we introduce three classical theoretical stances within the field of mathematics education. These are used to highlight the shift in how representations are conceived and studied in mathematics education, and its impacts on further developing both pedagogy and theory in this field.

First, we need to make explicit the context – both past and present – in which we are writing this contribution. All three authors were educated, and currently live, in cultures that assume (either explicitly or implicitly) that mathematical objects have a Platonic nature. By this we mean that they are commonly taken as existing in some not directly accessible reality from which “shadows” are cast; such shadows are the imperfect forms with which we can access the “real” perfect objects behind them, in order to talk and think about them. Indeed, the verb “to represent” comes from the Latin word “repraesentare”, formed from the prefix “re-” expressing intensive force, or reiteration, and the verb “praesentare” that means “to present”. So to represent entails the idea of something being “out there”, and that this something may be realized again through one or more representations that manifest some aspects of it. Coherently with this metaphor, we learn to talk and think about mathematical objects by interacting with their representations. However, frequently, as expert mathematicians it happens that we become so comfortable with particular representations that we forget that they are not actually the object they stand for (see, for example, Figure ⁠3⁠). This can cause significant difficulties in the teaching and learning of mathematics.

The Platonic philosophical stance outlined above is at the basis of much of the research on mathematical representations, which intersects with mathematics education from various fields of research. Various theories on learning mathematics hold it to be key to appropriately use mathematical representations and master their mutual relationships by understanding the mathematical objects they represent, by somehow tapping on their “true” meanings. However, the relationships between mathematical objects, their meanings and their representations are conceptualized and operationalized differently by different researchers and theoretical frameworks. In the following paragraphs we briefly highlight: (1) three key positions from the diversity of theoretical frameworks that have been conceived and used to study mathematical representations, and (2) a shift in how representations are conceived and studied in the field of mathematics education, moving towards the importance of how we talk about (representations of) mathematical objects. We then discuss how such a shift could have an impact on both the practice of teaching and learning mathematics, and on theorizing representations. The three key positions selected are those of Goldin, Duval and Sfard.

Position of Goldin

One influential and essentially pragmatic view of mathematical representations in educational contexts is Goldin’s, which firstly distinguishes external from internal representations. The former are often visible or tangible productions such as graphs, arrangements of concrete objects or manipulatives, words, formulas, etc. (although could also include, e.g., communications in speech or gesture) that encode, stand for, or embody mathematical ideas or relationships [⁠12⁠ G. A. Goldin, Mathematical representations. In Encyclopedia of Mathematics Education, 2nd ed., edited by S. Lerman, Springer, 566–572 (2020) ], and aim to communicate them to others or to one’s future self. Collected external representations of these types and many more form much of the data used in empirical research by members of our group and others. We cannot (yet!) observe anyone’s internal mathematical representations directly, but we may make inferences about learners’ internal representations on the basis of their interaction with, production of, or discourse regarding external representations, and to some extent, descriptions, for example, of their mental imagery while problem-solving. These forms might include the mental manipulation of systems of verbal/syntactic, imagistic, and formal notational configurations (or other less frequently discussed forms, such as auditory and/or kinaesthetic rhythmic patterns), which while invisible to the observer, may be inferred [⁠13⁠ G. Goldin and N. Shteingold, Systems of representations and the development of mathematical concepts. In The Roles of Representation in School Mathematics, edited by A. A. Cuoco and F. R. Curcio, NCTM, 1–23 (2001) ]. Further, Goldin’s view is that any mathematical representation cannot be understood in isolation, but only as part of an interconnected structure of meanings, ideas, systems and practices, which refer to each other in multiple and complex ways.

The relationships between internal and external representations must clearly be bidirectional (i.e. one can recreate and manipulate previously seen imagery in the mind’s eye, or recreate and develop one’s mental imagery on paper or computer screen, for example); this interaction between internal and external representation is fundamental to effective teaching and learning [⁠11⁠ G. A. Goldin, Systems of representations and the development of mathematical concepts. In The Roles of Representations in School Mathematics, edited by A. A. Cuoco and F. R. Curcio, NCTM, Reston, VA, 1–23 (2001) , ⁠13⁠ G. Goldin and N. Shteingold, Systems of representations and the development of mathematical concepts. In The Roles of Representation in School Mathematics, edited by A. A. Cuoco and F. R. Curcio, NCTM, 1–23 (2001) ]. Teaching mathematics is thought to happen most effectively “when we understand the effects on students’ learning of external representations and structured mathematical activities” [⁠13⁠ G. Goldin and N. Shteingold, Systems of representations and the development of mathematical concepts. In The Roles of Representation in School Mathematics, edited by A. A. Cuoco and F. R. Curcio, NCTM, 1–23 (2001) , p. 19] – yet to do this, it is vital to discuss students’ internal representations and how these are connected to one another. The conclusion is that the fundamental goals of mathematics education must include the development of coherent internal systems of mathematical representation that interact effectively with established external systems.

One further point that we would highlight from Goldin’s work over the years on internal-external representational relationships is its relation to the pedagogic perspectives of behaviourism and constructivism, which are often presented as diametric opposites or, at least, in conflict. Behaviourist principles exclude any inference about the internal. Resulting pedagogies focus on instructional programmes for shaping learners’ behaviour through conditioning [⁠9⁠ F. Furinghetti, J. M. Matos and M. Menghini, From mathematics and education, to mathematics education. In Third International Handbook of Mathematics Education, edited by M. A. (Ken) Clements, A. J. Bishop, C. Keitel, J. Kilpatrick and F. K. S. Leung, Springer, 273–302 (2013) ] – essentially, their acquiring, reproducing and carrying out of procedures with certain external representational forms according to a prescribed set of rules, with clearly measurable results. Constructivist principles, in contrast, strongly emphasize the internal – in particular the radical constructivist movement, according to which any individual only has access to their own perceived experiences, not to any definitive “real world” [⁠10⁠ E. von Glasersfeld, An exposition of constructivism: why some like it radical. In Constructivist Views on the Teaching and Learning of Mathematics, edited by R. B. Davis, C. A. Maher and N. Noddings, National Council of Teachers of Mathematics, Reston, VA, 19–29 (1990) ]. Resulting pedagogies focus on learners’ discoveries and conceptualizations, often through solo or group problem-solving activity. Research in mathematics education which draws on Goldin’s view, then, by centring the interactions between a variety of internal and external representations, has potential to include insights and elements of both perspectives. In terms of pedagogy, this would mean emphasizing “skills and correct answers as well as complex problem solving and mathematical discovery, without seeing these as contradictory” [⁠13⁠ G. Goldin and N. Shteingold, Systems of representations and the development of mathematical concepts. In The Roles of Representation in School Mathematics, edited by A. A. Cuoco and F. R. Curcio, NCTM, 1–23 (2001) , p. 8].

Position of Duval

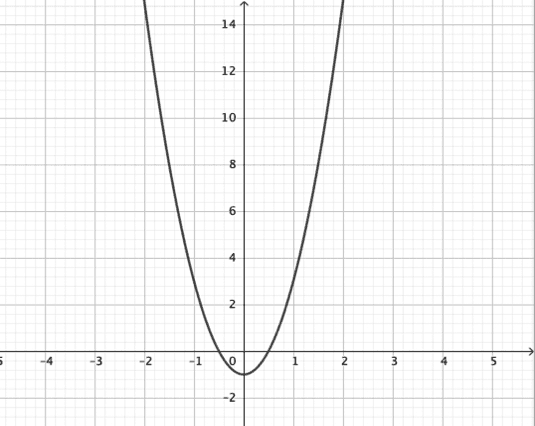
Duval’s position stems from the assumption that mathematics is epistemologically different from any other discipline because, as discussed above, mathematical objects are not directly accessible: they can be accessed only indirectly through their representations. Unlike in the case of a person, where any representation of aspects of her could be directly compared to her actual physical form, in the case of mathematical objects no juxtaposition between a representation and the object itself is possible [⁠5⁠ R. Duval, Understanding the mathematical way of thinking – the registers of semiotic representations. Springer International Publishing AG (2017) ]. Therefore, it is extremely difficult to distinguish representations of objects from the objects they represent, but also to (learn to) recognize that multiple different representations may refer to the same mathematical object. This is especially true in cases in which the representations make use of very different units of meaning: for example, “$f(x)=4x^2-1$”, in which the units of meaning are determined by the algebraic inscriptions on the left and right of the “$=$” sign, and a graph such as the one shown in Figure ⁠4⁠, in which the units of meaning are graphical elements such as the points of the parabola, its intersections with the $x$-axis, and so on.

To overcome this situation, and thus gain new knowledge about the mathematical objects referred to and solve problems, it is necessary to (learn to) transform one representation into another. Duval introduces the notion of register of semiotic representation [⁠5⁠ R. Duval, Understanding the mathematical way of thinking – the registers of semiotic representations. Springer International Publishing AG (2017) ] to discuss and analyse this transforming activity that lies at the heart of doing mathematics. In order to be a register, a semiotic system (a system of signs) needs to allow the production of representations that provide (indirect) access to mathematical objects, “explore all that is possible” with such signs, and “open a field of specific operations that allow transforming the produced representations into new representations” [⁠5⁠ R. Duval, Understanding the mathematical way of thinking – the registers of semiotic representations. Springer International Publishing AG (2017) , p. 68].

For example, a register of semiotic representation that Duval has discussed extensively in his work, is the register of figures, used heavily in geometry, and developed in order to produce representations that allow us to gain insight and reason about geometrical objects. Just like for any other register, using the register of figures is based on specific cognitive operations, specifically: recognizing at a glance the shapes in the figure, recognizing the figure as being similar to the shapes of real objects, realizing that there are several ways to interpret the shapes or the figural units. A key property of figural units is their dimension. Duval argues that “seeing” geometrically means operating dimensional deconstruction of the shapes, and being able to shift quickly from units of one dimension to those of another, to recognize the relationships between the various figural units. So, within the register of figures, one representation can be transformed into another through dimensional deconstruction and reorganization of the figural units.

More generally, a register of semiotic representation has its specific units of meaning (which in the case of the register of figures would be figural units) and a representation can be transformed into another in the same register through processes of treatment (e.g., dimensional deconstruction in the register of figures). However, according to Duval, the only way to distinguish representations of an object from the object itself is to use at least two registers and to be able to convert from one to the other [⁠5⁠ R. Duval, Understanding the mathematical way of thinking – the registers of semiotic representations. Springer International Publishing AG (2017) , ⁠6⁠ R. Duval, Registers of semiotic representation. Mathematical representations. In Encyclopedia of Mathematics Education, 2nd ed., edited by S. Lerman, Springer, 724–727 (2020) ]. In the case of geometry, but also the other subfields in mathematics, another fundamental register is that of natural language. Algebra and Analysis make use of the register of symbolic expressions and the graphical register of the Cartesian plane (e.g., Figure ⁠4⁠).

Formally, a semiotic representation is denoted by the couple: (register used, merged meaning units) [⁠6⁠ R. Duval, Registers of semiotic representation. Mathematical representations. In Encyclopedia of Mathematics Education, 2nd ed., edited by S. Lerman, Springer, 724–727 (2020) , p. 724]. Understanding in mathematics, according to Duval, means being able to coordinate registers, in his words: “understanding mathematical concepts presupposes awareness of the cognitive one-to-one mapping operation between relevant meaningful units of two registers at least” [⁠6⁠ R. Duval, Registers of semiotic representation. Mathematical representations. In Encyclopedia of Mathematics Education, 2nd ed., edited by S. Lerman, Springer, 724–727 (2020) , p. 726]. In the example of the function in Figure ⁠4⁠, treatments in the algebraic register could be rewriting the algebraic expression as $(2x-1)(2x+1)$ to highlight the function’s “zeros” (obtained solving $(2x-1)(2x+1)=0$). Conversion into the graphical Cartesian coordinates register that corresponds to such algebraic treatments could correspond to a dimensional deconstruction of the graph (treatment), to visualize the two intersections with the $x$-axis: $(-\frac{1}{2},0)$, $(\frac{1}{2},0)$.

Position of Sfard – a shift in perspectives

Taking a Vygotskian socio-constructivist perspective, and following Wittgenstein, Sfard [⁠19⁠ A. Sfard, Thinking as communicating: human development, the growth of discourses, and mathematizing. Cambridge University Press (2008) , ⁠20⁠ A. Sfard, Commognition. In Encyclopedia of Mathematics Education, edited by S. Lerman, Springer, Cham (2018) ] sees mathematical objects as no longer residing in some hyper-reality, but in discourse itself, being part of an autopoietic system, a system that defines its own objects. Hence, their meaning stems from the ways in which realizations of a mathematical object are used discursively; an implication is that the term ’representation’ is inappropriate, as she rejects the Platonic view of mathematical objects existing “out there” and being re-presented in discourse. Rather, under her Commognitive Framework mathematical objects “come to life” as part of a discourse of human communities.

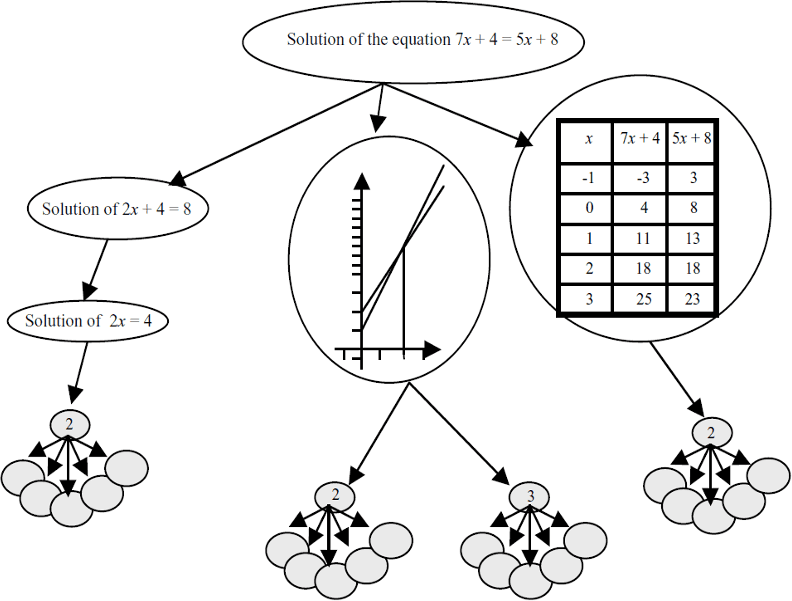
Another difference between realizations and representations can be found in how ’realization’ acquires a psychological component: the same physical (graphical, tangible or gestural) production may be a realization of a mathematical object for one person and not for someone else, depending on the phase each person is at in their discursive construction of the mathematical object in question. For example, for an expert $f(x)=3+2x$ may be a realization of a real valued function (of which another realization might be its graph on the Cartesian plane), but for a learner who is not yet familiar with the discourse about either real functions or complex numbers, it is just a strange equality that mixes letters and numbers. Sfard [⁠19⁠ A. Sfard, Thinking as communicating: human development, the growth of discourses, and mathematizing. Cambridge University Press (2008) ] used the term realization as follows: “Realization of the signifier $S$ is a perceptually accessible thing $S^{\prime }$ so that every endorsed narrative about $S$ can be translated according to well defined rules into an endorsed narrative about $S^{\prime }$” [⁠19⁠ A. Sfard, Thinking as communicating: human development, the growth of discourses, and mathematizing. Cambridge University Press (2008) , p. 154]. Sfard sees the relations signifier-signified (between $S$ and $S^{\prime }$) as symmetrical. So, for example, while the graph shown in Figure ⁠4⁠ could be a signifier of the symbolic expression $y=(2x+1)(2x-1)$, one could also talk about that graph as signifying the symbolic expression. A realization of a signifier can be accomplished through several discourses. For example, the graph shown in Figure ⁠4⁠ and the symbolic expression $y=(2x+1)(2x-1)$ are two realizations of a quadratic function, the first being a signifier in a visual-graphical discourse while the second is a signifier in a symbolic discourse. Generally, for an expert, a quadratic function as a signifier could be realized (or signified) via a table of numbers, symbolic expressions, graphical drawing and more. The way we talk about tables of values, graphs or algebraic expressions is different, as each of them belongs to a different discourse. A learner needs to be able to participate in these different discourses, but also to “same” them into a unified discourse about quadratic functions. The richness of realizations for a signifier can be captured by a realization tree (Figure ⁠5⁠).

Discussion: The shift in perspectives and some implications

In all three perspectives, representations (or realizations) of mathematical objects are essential in mathematical thinking, teaching and learning, to the extent that no mathematical understanding (or discourse) is possible without them! In Goldin’s perspective there is a key dialectic between internal and external representations: teaching mathematics most effectively happens when we understand students’ learning of external representations and structured mathematical activities and effectively make use of such an understanding to influence their internal representations. For Duval a fundamental and necessary process in mathematical learning and understanding is that of conversion from one register of semiotic representation to another. Moreover, Duval’s theory explicitly stands on the assumption that mathematical objects are not directly accessible, which suggests their existence in some inaccessible-to-us reality. As discussed earlier, this is a typical philosophical stance that is arguably present in other theoretical perspectives, including that of Goldin. In Sfard’s approach, however, an important shift seems to occur: mathematical objects no longer exist anywhere other than in discourse itself. Therefore, to “know” a mathematical object means to be able to talk about it through narratives accepted within a community of mathematicians, and through discursive practices, we learn to recognize and express realizations of such an object.

Therefore, in Sfard’s theory, a very important process consists in coming to see two “things” that we previously saw as different as the same, that is, as realizations of the same discursive object. A way into understanding students’ mathematical learning, in this perspective, is through their discourse, and by the identification of patterns in what is said and done. This perspective opens new avenues of research, providing analytical tools for observing teaching and learning practices not only in contexts in which canonical representations are “presented” to the students, but also in settings in which students are invited to “invent” their own [⁠3⁠ A. A. Cuoco and F. R. Curcio, The roles of representations in school mathematics. NCTM, Reston, VA (2001) ], or make sense of feedback stemming from interactions with a range of physical or digital artefacts. In line with this thinking, as educators we need to stay open to multiple creative realizations, and not lock the curriculum to a narrow selection of standardized representations, while disallowing or “hiding” others. This is particularly important when considering the diversity of the learner population, who to different extents may need to access different kinds of realizations in “non-standard” ways. As examples, think of the ways in which a blind student might realize function through non-visual sensory forms, or how mathematical discourse would be different under the grammars of signed compared to spoken language.

Moreover, we see some similarities between Sfard’s shift away from a Platonic conception of mathematical objects and their representations, and the position advanced by Schoenfeld [⁠18⁠ A. H. Schoenfeld, Classroom observations in theory and practice. ZDM Mathematics Education 45, 607–621 (2013) ] and Li [⁠14⁠ Y. Li and A. H. Schoenfeld, Problematizing teaching and learning mathematics as “given” in STEM education. Int. J. Stem. Educ. 6, 1–13 (2019) ], who in their Teaching for Robust Understanding Framework take an Aristotelic stance, arguing in favour of “empirical” mathematics. That is, mathematics can and should be seen as a set of products created through experience (as opposed to pre-existing in an inaccessible realm). This perspective allows for what they (and we) see as a necessary focus on students’ experience, in which pedagogy is not conceived of as “what should the teacher do” so much as “what mathematical experiences should students have in order for them to develop into powerful thinkers?” [⁠14⁠ Y. Li and A. H. Schoenfeld, Problematizing teaching and learning mathematics as “given” in STEM education. Int. J. Stem. Educ. 6, 1–13 (2019) , p. 8]. For mathematical experiences to accomplish this, Li and Schoenfeld argue that they need to provide not only opportunities for making sense of the mathematics at stake, but also – and perhaps more importantly because education has focused less on this – they need to involve sense-making processes [⁠15⁠ W. McCallum, Sense-making and making sense, blogs.ams.org/ matheducation/2018/12/05/sense-making-and-making-sense/ (2018) ], highlighting “the importance for students to experience mathematics through creating, designing, developing, and connecting mathematical ideas” [⁠14⁠ Y. Li and A. H. Schoenfeld, Problematizing teaching and learning mathematics as “given” in STEM education. Int. J. Stem. Educ. 6, 1–13 (2019) , p. 6]. Many educational experiences of this sort involve the use of physical or (more recently) digital artefacts that provide interactive and/or dynamic representations (which may be or become realizations of mathematical objects for the students).

As an example, consider the following task, explored by Sinclair [⁠21⁠ N. Sinclair, Computer-based technologies and plausible reasoning. In Making the Connection: Research and Teaching in Undergraduate Mathematics Education, edited by M. Carlson and C. Rasmussen, Mathematical Association of America, 233–244 (2008) ]: take the three vertices of a triangle $ABC$ and reflect them each across the opposite side of the triangle to obtain a new “reflex” triangle $DEF$; then iterate the process applying the reflection to triangle $DEF$, and so on. This problem can be approached in many different ways, involving different representations. We argue that working in a dynamic geometry environment (like Geometer’s Sketchpad, Cabri Géomètre, GeoGebra, Desmos, etc.) can offer many students access into mathematical reasoning through sense-making processes. In this problem, for example, Sinclair explains how she used The Geometer’s Sketchpad to explore a typical conjecture, that is, that the reflections eventually converge to an equilateral triangle. The software allowed her to iteratively reflect an arbitrary triangle and compute its measurements, effortlessly. Dragging vertex $A$ led her to quickly realize that the conjecture was false: $DEF$ can degenerate into a straight line. Moreover, she noticed that “$DEF$ seemed to change in a very chaotic way” as she dragged $A$. Eventually, choosing a measure for how close to being equilateral each triangle was (in this case perimeter squared over area, which has a minimum for equilateral triangles), and creating overall pictures of the changing measurement like those in Figure ⁠6⁠, she found confirmation of the chaotic behaviour. The splitting of the “branches” confirms that small changes in the position of point $A$ can give rise to radically different reflex triangles. But the symmetries of the branches also show regularity in the chaos, leading to new conjectures to be proved.

These sorts of experiences, that rely heavily on the interactive representations produced by software, are valuable for learners across the spectrum of mathematical capacities and needs. We note that in particular they may offer the possibility to “open doors” into participation in mathematical discourse: indeed, these tools offer students concrete-enough “things” to interact with and make sense of, allowing them to meaningfully start participating to mathematical discourse, without the need of formal language from the start. Recent studies suggest that through these means students who otherwise would remain excluded from mathematical discourse, actually find insightful ways to start participating to it (e.g., [⁠1⁠ A. Baccaglini-Frank, To tell a story, you need a protagonist: how dynamic interactive mediators can fulfill this role and foster explorative participation to mathematical discourse. Educ. Stud. Math. 106, 291–312 (2021) , ⁠8⁠ C. Finesilver, L. Healy and A. Bauer, Supporting diverse approaches to meaningful mathematics: from obstacles to opportunities. In Enabling Mathematics Learning of Struggling Students: International Perspectives, edited by Y. P. Xin, R. Tzur and H. Thouless, Springer (in press) ]).

This takes us back to the pressing need to conceive theoretical languages that allow consistent “talking about” dynamism in representations [⁠2⁠ A. Baccaglini-Frank, C. Finesilver, S. Okumus and M. Tabach, Introduction to the work of TWG24: representations in mathematics teaching and learning. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (Utrecht, 2019), Utrecht, Netherlands, hal-02394695 (2019) , ⁠1⁠ A. Baccaglini-Frank, To tell a story, you need a protagonist: how dynamic interactive mediators can fulfill this role and foster explorative participation to mathematical discourse. Educ. Stud. Math. 106, 291–312 (2021) ]. Imagine, for example, a theoretical language through which we could differentiate between representing/realizing a mathematical phenomenon through dragging a finger over a touch screen, versus representing/realizing the same mathematical phenomenon with ones’ whole body – or recalling those embodied experiences in one’s mind when later encountering that mathematical idea in a different form.

We are not arguing that the theoretical lens of Commognition is the solution to this open problem; indeed, much research is still needed, and some is being carried out as we write. For example, a special issue of the journal Digital Experiences in Mathematics Education (in preparation) has been devoted to research “supporting transitions within, across and beyond digital experiences for the teaching and learning of mathematics”, in which a variety of theoretical approaches are used to describe and study the three types of transition (within, across and beyond digital experiences). However, Sfard’s perspective seems to embody an important shift that leaves behind the contradictory binary of the inaccessible-to-us world of perfect mathematical objects and the “real world” with its messy experiences in which we learn to recognize and produce realizations. Instead, it puts discourse, i.e. what is said and done by the community of all those who do mathematics, right at the forefront.

Acknowledgements We wish to graciously thank Al Cuoco for the feedback he has generously offered us through numerous discussions on drafts of this paper.

Anna Baccaglini-Frank is an associate professor at the Department of Mathematics of the University of Pisa, Italy. Her main research interests are in technology-enhanced learning at all grade levels. Among other activities, she serves on the editorial board of Educational Studies in Mathematics, is an associate editor of Digital Experiences in Mathematics Education, and leads a the Thematic Working Group 24: “Representations in Mathematics Teaching and Learning” at the congress of the European Society for Research in Mathematics Education (ERME). anna.baccaglinifrank@unipi.it Carla Finesilver is a senior lecturer at King’s College London. Her research interests are in mathematics education and inclusive education, in particular improving accessibility for diverse learners. She is a co-editor of the special issue of Digital Experiences in Mathematics “Supporting transitions within, across and beyond digital experiences for the teaching and learning of mathematics”, currently under development, and co-leads the CERME Thematic Working Group 24. carla.finesilver@kcl.ac.uk Michal Tabach is professor at the School of Education, Tel Aviv University, and researcher in mathematics education. Her main research interests are integrating technology to enhance teaching and learning of mathematics at all levels, and knowledge shifts in the mathematics classroom. She has been Secretary of PME, the international group of Psychology of Mathematics Education. She is currently an associate editor of Educational Studies in Mathematics. She co-leads the CERME Thematic Working Group 24. tabachm@tauex.tau.ac.il

References

1. A. Baccaglini-Frank, To tell a story, you need a protagonist: how dynamic interactive mediators can fulfill this role and foster explorative participation to mathematical discourse. Educ. Stud. Math. 106, 291–312 (2021)
2. A. Baccaglini-Frank, C. Finesilver, S. Okumus and M. Tabach, Introduction to the work of TWG24: representations in mathematics teaching and learning. In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (Utrecht, 2019), Utrecht, Netherlands, hal-02394695 (2019)
3. A. A. Cuoco and F. R. Curcio, The roles of representations in school mathematics. NCTM, Reston, VA (2001)
4. E. Deliyianni, A. Monoyiou, I. Elia, C. Georgiou and E. Zannettou, Pupils’ visual representations in standard and problematic problem solving in mathematics: their role in the breach of the didactical contract. European Early Childhood Education Research Journal 17, 95–110 (2009)
5. R. Duval, Understanding the mathematical way of thinking – the registers of semiotic representations. Springer International Publishing AG (2017)
6. R. Duval, Registers of semiotic representation. Mathematical representations. In Encyclopedia of Mathematics Education, 2nd ed., edited by S. Lerman, Springer, 724–727 (2020)
7. C. Finesilver, Low-attaining students’ representational strategies: tasks, time, efficiency, and economy. Oxford Review of Education 43, 482–501 (2017)
8. C. Finesilver, L. Healy and A. Bauer, Supporting diverse approaches to meaningful mathematics: from obstacles to opportunities. In Enabling Mathematics Learning of Struggling Students: International Perspectives, edited by Y. P. Xin, R. Tzur and H. Thouless, Springer (in press)
9. F. Furinghetti, J. M. Matos and M. Menghini, From mathematics and education, to mathematics education. In Third International Handbook of Mathematics Education, edited by M. A. (Ken) Clements, A. J. Bishop, C. Keitel, J. Kilpatrick and F. K. S. Leung, Springer, 273–302 (2013)
10. E. von Glasersfeld, An exposition of constructivism: why some like it radical. In Constructivist Views on the Teaching and Learning of Mathematics, edited by R. B. Davis, C. A. Maher and N. Noddings, National Council of Teachers of Mathematics, Reston, VA, 19–29 (1990)
11. G. A. Goldin, Systems of representations and the development of mathematical concepts. In The Roles of Representations in School Mathematics, edited by A. A. Cuoco and F. R. Curcio, NCTM, Reston, VA, 1–23 (2001)
12. G. A. Goldin, Mathematical representations. In Encyclopedia of Mathematics Education, 2nd ed., edited by S. Lerman, Springer, 566–572 (2020)
13. G. Goldin and N. Shteingold, Systems of representations and the development of mathematical concepts. In The Roles of Representation in School Mathematics, edited by A. A. Cuoco and F. R. Curcio, NCTM, 1–23 (2001)
14. Y. Li and A. H. Schoenfeld, Problematizing teaching and learning mathematics as “given” in STEM education. Int. J. Stem. Educ. 6, 1–13 (2019)
15. W. McCallum, Sense-making and making sense, blogs.ams.org/ matheducation/2018/12/05/sense-making-and-making-sense/ (2018)
16. N. C. Presmeg, Preface, In Representations and Mathematics Visualization, edited by F. Hitt, North American Chapter of the International Group for the Psychology of Mathematics Education, ix–xvi (2002)
17. E. Robotti, A. Baccaglini-Frank, G. Sensevy and T. Fritzlar, TWG24: representations in mathematics teaching and learning. Introduction to the papers of TWG24. In Proceedings of CERME 10 (Dublin, 2017), hal-01950557 (2017)
18. A. H. Schoenfeld, Classroom observations in theory and practice. ZDM Mathematics Education 45, 607–621 (2013)
19. A. Sfard, Thinking as communicating: human development, the growth of discourses, and mathematizing. Cambridge University Press (2008)
20. A. Sfard, Commognition. In Encyclopedia of Mathematics Education, edited by S. Lerman, Springer, Cham (2018)
21. N. Sinclair, Computer-based technologies and plausible reasoning. In Making the Connection: Research and Teaching in Undergraduate Mathematics Education, edited by M. Carlson and C. Rasmussen, Mathematical Association of America, 233–244 (2008)