This article gives an overview of the Irish secondary school Transition Year programme and in particular how the teaching and learning of mathematics is situated within it.

1 Introduction

Second-level education in Ireland caters for students between 12 and 18 years of age. It consists of two cycles, the Junior Cycle and Senior Cycle. The 3-year Junior Cycle prepares students for state examinations in the core subjects of Mathematics, Irish and English, as well as in students’ individually chosen subjects. Following the Junior Cycle, students have the option of enrolling on a 1-year Transition Year (TY) programme or progressing directly to the Senior Cycle. The 2-year programme of the Senior Cycle culminates in the terminal state examination, the Leaving Certificate, a qualification which heavily influences the destination of students for further education and training.

In this article, we give an overview of the TY programme and consider the potential for introducing some interesting mathematics within it. TY is an optional extra year of study that is taken up by the majority of students before embarking on two years of study for the Leaving Certificate⁠1⁠According to [⁠2⁠ A. Clerkin, Personal development in secondary education: the Irish Transition Year. Education Policy Analysis Archives 20.38 (2012) ], about 55 % of students took TY in 2010/11. Although there is consensus that there is an upward trend in participation rates, no data is currently available to confirm this.. The official mission of TY is [⁠6⁠ National Council for Curriculum and Assessment, Transition Year programmes – guidelines for schools, ncca.ie/en/resources/ty_transition_year_school_guidelines/ (2021) , p. 3]:

To promote the personal, social, educational and vocational development of pupils and to prepare them for their role as autonomous, participative, and responsible members of society.

2 The Transition Year curriculum

It is government policy that each school design its own TY programme to meet the needs of its students. However, the Department of Education (the government ministry responsible for education) has produced guidelines as to what such a programme should entail. Four areas of learning are suggested [⁠8⁠ Professional Development Service for Teachers, TY Curriculum, pdst.ie/TY/curriculum (2021) ]:

  1. Core: This includes Mathematics along with English, Irish, Information Technology and Physical Education

  2. Subject sampling: These may be taster modules in subjects to help students decide on subject choices for Leaving Certificate. Students may also be exposed to subjects that they have not studied before e.g. Environmental Studies, Japanese, Arabic, Drama, Photography, Global Development

  3. TY-specific: Study and activities which allow students to pursue their own interests and to contribute to their local communities e.g. social entrepreneurship, charitable activities

  4. Calendar: Work experience, foreign exchange visits, sporting activities, visiting speakers, drama/musical production

Over the years the programme has been very well received amongst students, parents, guardians and teachers alike and is considered unique in that there is no similar programme offered in education systems of other countries [⁠2⁠ A. Clerkin, Personal development in secondary education: the Irish Transition Year. Education Policy Analysis Archives 20.38 (2012) ]. In its 2020 report on education in Ireland, the OECD commended the programme as it “allows students to sample different subjects and undertake work experience and other projects, and helps guide them in choosing their upper secondary education subjects and future career path” [⁠7⁠ Organisation for Economic Co-operation and Development, Education in Ireland: an OECD assessment of the senior cycle review, oecd.org/ireland/education-in-ireland-636bc6c1-en.htm (2020) ].

For students, TY may be viewed as an academically low-risk interlude between state examinations because there is no state-level assessment of student performance. Many schools do issue individual assessment certificates that rate student attainment across the programme but these marks generally do not count towards future progression.

3 Scope of TY mathematics

There is no prescribed syllabus for mathematics in TY and so, theoretically at least, teachers have great flexibility regarding the mathematics they present to their students. Government does not give specific recommendations as to what should be taught but a 2011 circular called for schools “to provide innovative learning opportunities and increased mathematics teaching hours to the extent feasible” in Transition Year [⁠3⁠ Department of Education, Circular 0058/0011, education.ie/ (2011) ]. Up to 2012, there had been very little information available on the content of TY mathematics programmes being delivered in schools, how they were delivered and the time spent on delivery. Then, as part of PISA 2012, a national survey of TY mathematics teachers was conducted.

3.1 PISA 2012 National Survey of TY Mathematics Teachers

Mathematics teachers were invited to complete questionnaires which focussed on concerns about the quality of TY mathematics offerings. In total, 1321 questionnaires were completed, an 80 % response rate, and the findings were reported in [⁠5⁠ G. Moran et al., Mathematics in Transition Year: insights of teachers from PISA 2012, erc.ie/documents/p12ty_maths_report.pdf (2013) ]. In the survey, teachers were asked to rate their level of agreement or disagreement with statements about the purpose of TY mathematics. It was found that only 31 % of teachers strongly agreed that one purpose of TY mathematics is to increase students’ confidence in their problem-solving ability, and only 34 % strongly agreed that one purpose was to encourage greater interest in mathematics. Almost 40 % disagreed or strongly disagreed that one purpose of TY mathematics is to familiarise students with the history of mathematics. These results were certainly out of kilter with government guidelines, as set out in [⁠4⁠ Department of Education, Transition Year programmes – guidelines for schools, education.ie/en/Schools-Colleges/Information/Curriculum-and-Syllabus/Transition-Year-/ty_transition_year_school_guidelines.pdf (1993) ], which state that these particular aspects of mathematics should be emphasised during TY. More importantly perhaps, they indicate a strong lack of agreement amongst teachers as to the purpose of teaching mathematics during TY.

3.2 Teaching resources and challenges

The national survey found that there was a great deal of variation in terms of resources that TY maths teachers used. Some teachers used textbooks from the Junior Cycle to consolidate previously covered content while others mined the Internet for engaging and challenging material. There was also evidence of teaching the Leaving Certificate syllabus, something the government guidance expressly discourages.

In the period from 2012 to 2018, we have had the opportunity of meeting with many TY teachers during outreach activities in secondary schools across Ireland. Teachers regularly commented on their struggle to engage students with mathematics, especially during TY. They reported that one view commonly held by students was that maths would not be relevant to their lives once their secondary schooling came to an end. Teachers agreed on the need for a book or module which would focus on the importance of the subject in the everyday world, introduce genuinely interesting ideas and also include some history of mathematics. The challenge of stoking the interest of teenagers who were sceptical about the global importance of maths (as well as a concern for students with genuine mathematical curiosity), encouraged us to write a book of projects to engage the interest of TY students⁠2⁠MIghTY Maths was published in October 2021 by Curriculum Development Unit, Mary Immaculate College, Limerick. Each topic can be investigated either in teacher-led lessons or in a guided project by the individual student or groups of students. The book is available for purchase at www.curriculumdevelopmentunit.com.. Exercises would need to be recreational as well as challenging in order to enthuse the target audience. In the next section, we present one of the topics presented in the book.

4 Divisibility of integers – an interesting topic for TY

At the teacher training college where we work, it sometimes happens that a student teacher will express their delight to learn for the first time, during an elementary number theory course, that divisibility of a number by 3 can be determined by checking if the sum of its digits is divisible by 3. They may wonder why they had not learned this rule earlier in their careers or why their school knowledge was restricted to rules for 2, 5 and 10. In any case, the topic of divisibility appeared to be a good one for TY students and student teachers alike.

Like the rule for 3, there exists a similar rule for the divisibility of a number by 9 and it forms the basis of a wonderful trick called Mindreader, which appeared in [⁠1⁠ C. Budd and C. Sangwin, Mathematics galore! Oxford University Press (2001) ] and is used in a project on number tricks in our book.

Mindreader

The “mindreader” asks a volunteer to

  1. pick any five-digit number where not all digits are the same and keep this number secret;

  2. jumble up the digits to get a new number;

  3. subtract the smaller of these numbers from the larger;

  4. hide one of the digits, , in the answer,  making sure ;

  5. call out the other digits in the answer.

The “mindreader” pronounces the hidden digit to be .

In order to know what the hidden digit is, we need to understand some basic ideas.

Definition 1. The digital root of a number is the sum of all its digits.

Example 1. The digital root of is because .

There follow two mathematical facts.

Lemma 1 (Divisibility rule for ). Take any number . Let be the digital root of . Then is a multiple of is a multiple of .

Lemma 2. For any number , with digital root , is a multiple of .

Example 2. The digital root of is . We see that has digital root .

Armed with Lemmata ⁠1⁠ and ⁠2⁠, we can now look at understanding the details of how the trick Mindreader works. We follow the given steps for the volunteer:

  1. Pick any five-digit number where not all digits are the same. Let have digits , so

    Indeed, Lemma ⁠2⁠ tells us that any number equals its digital root plus some multiple of .

  2. Jumble up the digits to get a new number. Call the new number . Let have digits , for example, so

  3. Subtract the smaller of these numbers from the larger. Let us suppose that , so

    N.B. The number is divisible by . Therefore, by Lemma ⁠1⁠, its digital root is a multiple of .

  4. Hide one of the digits in your answer, , making sure the hidden digit is not a zero.

  5. Call out the remaining digits of the number .

    At this point, the “mindreader” has all but one of the digits that make up the digital root. All they need to do is add them and see what digit is required to sum to the next greatest multiple of . For example, if they are told the digits are , , and . These sum to . The next highest multiple of is so the hidden digit is . Or, if they are told the digits are , , and . These sum to , already a multiple of . Since it was specified that zero should not be hidden, they conclude that the hidden digit is .

Example 3. Here is a worked example. The volunteer

  1. picks the number ;

  2. jumbles the digits of to get the number ;

  3. computes ;

  4. hides the digit ;

  5. calls out the digits and .

Now the “mindreader” knows that , being a multiple of 9, has digital root a multiple of 9. They know that . Since the next multiple of 9 greater than 16 is 18, they conclude that . The “mindreader” pronounces that the hidden digit is .

Remark 1. The Mindreader trick shown here uses 5-digit numbers. Is there anything special about or would the trick work for any number of digits?

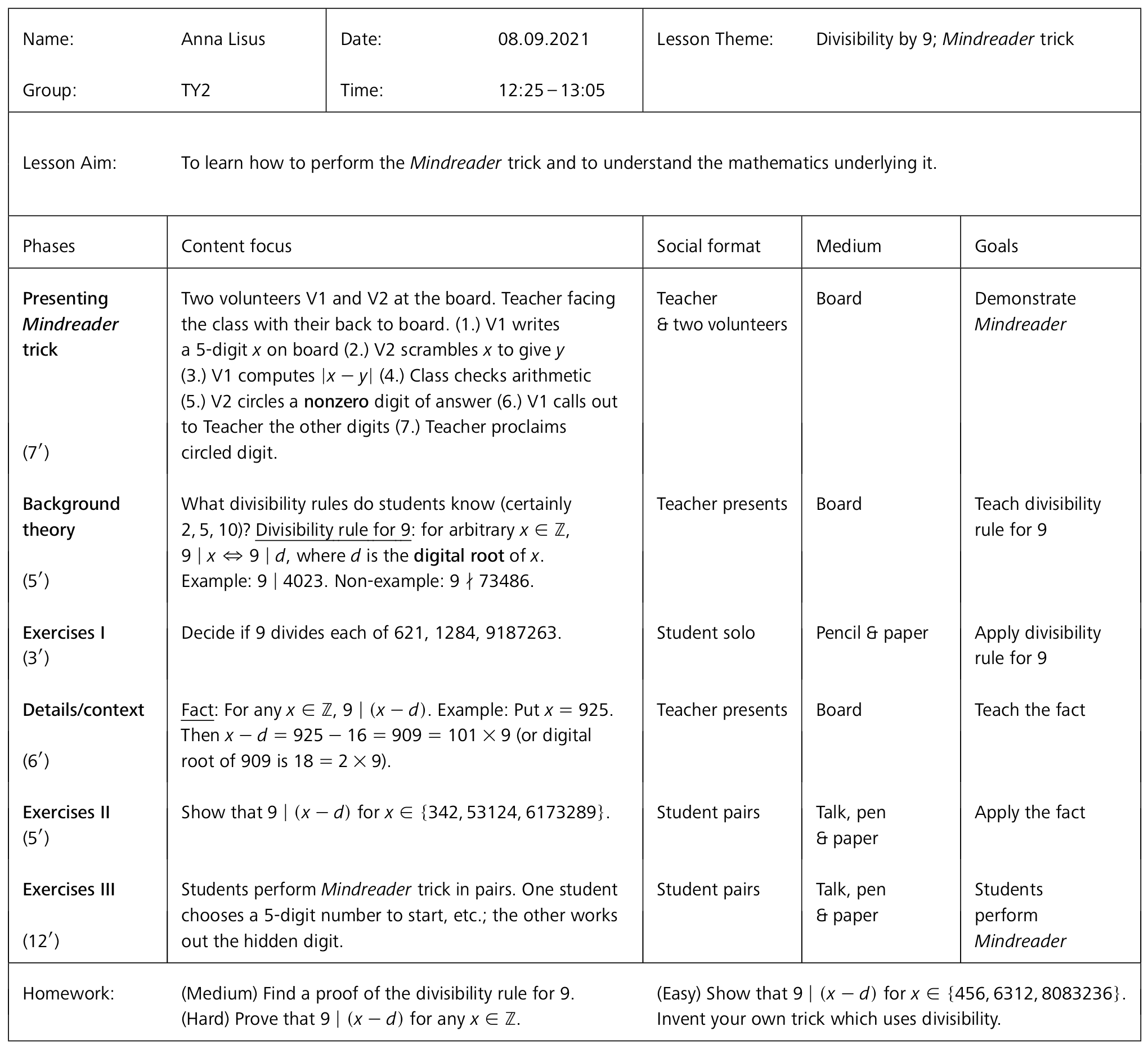
Finally, we give Table ⁠4⁠ as a sample detailed lesson plan for teaching the content of Mindreader.

5 Conclusion

The Transition Year programme in Irish secondary schools is a highly regarded programme. Maintaining the position of mathematics, a core subject in the programme, requires a great effort on the part of schools because there is no curriculum and guidelines on teaching content are rather vague. Individual teachers and schools go to great lengths to provide useful and interesting material, yet gaps clearly remain. We give an example of divisibility of integers as a topic that may engage TY students’ interest and we encourage the use of stimulating and recreational mathematical exercises and projects across the programme.

Ronan Flatley is Lecturer in Mathematics at Mary Immaculate College, Limerick, Ireland. He currently serves on the Committee of the Irish Mathematical Society. He is the author of MIghTY Maths, a book of maths projects for Transition Year students. ronan.flatley@mic.ul.ie

  1. 1

    According to [⁠2⁠ A. Clerkin, Personal development in secondary education: the Irish Transition Year. Education Policy Analysis Archives 20.38 (2012) ], about 55 % of students took TY in 2010/11. Although there is consensus that there is an upward trend in participation rates, no data is currently available to confirm this.

  2. 2

    MIghTY Maths was published in October 2021 by Curriculum Development Unit, Mary Immaculate College, Limerick. Each topic can be investigated either in teacher-led lessons or in a guided project by the individual student or groups of students. The book is available for purchase at www.curriculumdevelopmentunit.com.

References

  1. C. Budd and C. Sangwin, Mathematics galore! Oxford University Press (2001)
  2. A. Clerkin, Personal development in secondary education: the Irish Transition Year. Education Policy Analysis Archives 20.38 (2012)
  3. Department of Education, Circular 0058/0011, education.ie/ (2011)
  4. Department of Education, Transition Year programmes – guidelines for schools, education.ie/en/Schools-Colleges/Information/Curriculum-and-Syllabus/Transition-Year-/ty_transition_year_school_guidelines.pdf (1993)
  5. G. Moran et al., Mathematics in Transition Year: insights of teachers from PISA 2012, erc.ie/documents/p12ty_maths_report.pdf (2013)
  6. National Council for Curriculum and Assessment, Transition Year programmes – guidelines for schools, ncca.ie/en/resources/ty_transition_year_school_guidelines/ (2021)
  7. Organisation for Economic Co-operation and Development, Education in Ireland: an OECD assessment of the senior cycle review, oecd.org/ireland/education-in-ireland-636bc6c1-en.htm (2020)
  8. Professional Development Service for Teachers, TY Curriculum, pdst.ie/TY/curriculum (2021)

Cite this article

Ronan Flatley, Transition Year in the Irish school system: Challenges and opportunities for teaching and learning mathematics. Eur. Math. Soc. Mag. 123 (2022), pp. 41–44

DOI 10.4171/MAG/73
This open access article is published by EMS Press under a CC BY 4.0 license, with the exception of logos and branding of the European Mathematical Society and EMS Press, and where otherwise noted.
Back to Issue 123