The publication in Leiria, in 1496, of the Almanach perpetuum, with the astronomical tables of the Sephardi scholar Abraham Zacut (1452–1515), initiated the use of scientific typography in Portugal. The Almanach’s tables were calculated in Salamanca in the Alphonsine tradition with reference to the period 1473–1476 [4 J. Chabàs and B. R. Goldstein, Astronomy in the Iberian Peninsula: Abraham Zacut and the transition from manuscript to print. Transactions of the American Philosophical Society 90.2, American Philosophical Society, Philadelphia, PA (2000) ]. It was translated and edited by the Portuguese José Vizinho and printed by the Jewish typographer Abraham d’Ortas. It appeared just a few years after a first edition of the Torah of 1487, in a Hebrew printing press in Faro in the south of Portugal, and the Tratado de Confissom of 1489, which is the first Christian text in Portuguese and was printed in Chaves, in the north of the country [3 A. Alselmo, Origens da imprensa em Portugal. Imprensa Nacional-Casa da Moeda, Lisboa (1991) ]. It should be noted that the Gutenberg Bible, the first book ever printed in Europe, dates from 1455, and the first printing of Euclid’s Elements in 1482 was done by the printer Erhard Ratdolt in Venice, in a Latin edition containing the first geometric diagrams ever printed.
The Almanach perpetuum was the main incentive for the recent book exhibition Tipografia Matemática Portuguesa: 1496–1987, whose first edition [13 Tipografia Matemática Portuguesa: 1496–1987 – Catalogue (Portuguese), ipleiria.pt/sdoc/tipografia-matematica-portuguesa-1496-1987/] took place from July to October 2021, in the six-centuries-old Moinho de Papel in Leiria, a city in the centre of Portugal with an ancient 12th century castle, residence of kings and setting of several cortes (medieval parliaments). The city gave its name to a famous pine forest (Pinhal de Leiria), which supplied wood for the ships used in Portuguese navigation in the 15th and 16th centuries. The exhibition was an initiative of the city of Leiria in partnership with the Centro Internacional de Matemática and the Polytechnic Institute of Leiria. The Moinho de Papel is a historical building on the river Lis, and housed the first paper mill established in Portugal in 1411; this may well be relevant to the fact that Leiria was also one of the first Portuguese cities to have a printing press, and indeed the city where the first scientific book – which was also instrumental for navigation in the age of discoveries – was printed in Portugal 526 years ago.
All rights reserved.
The second date of the title of this unprecedented exhibition corresponds to the publication, coincidentally 500 years after the first book printed in Portugal, of the first volume of Portugaliae Mathematica to be electronically composed in TeX. With 32 significant original works in Portuguese mathematical typography, many of them rare books containing unknown or still barely known yet highly interesting pages, the exhibition presents nine sections that traverse the whole history of the mathematical sciences in Portugal, from the age of ocean navigation and the first European globalisation through military engineering, essential in the wars of Restoration (1640–1668) after the end of the Iberian Union, to the successive reforms of Colleges, Military Academies and Universities (1772 and 1911) and finally the scientific research of the 20th century.
Mathematical tables for navigation – arithmetical rules for overseas trade
The Almanach perpetuum is a landmark of the beginning of the culture of mathematical sciences in Portugal through the influence and use of the art and knowledge of navigation, namely in the first ocean voyages of Vasco da Gama to India and Pedro Álvares Cabral to Brazil [1 L. Albuquerque, Introdução, to the fac-simile edition of the Almanach Perpetuum. Imprensa Nacional-Casa da Moeda, Lisboa (1986) ]. It had several editions in the 16th century and it was used in the preparation of the Reportórios dos Tempos, a set of popular time calendars and almanacs also used in astrology; a certain Gaspar Nicolas participated in the elaboration of the one from the year 1518.
All rights reserved.
All rights reserved.
In 1519 in Lisbon, this Portuguese mathematician published his Tratado da pratica Darismetyca, a book of a technical and utilitarian nature about the rules of arithmetic, also “for overseas trade”; it went through ten new editions over the course of the next two centuries. In his preface, Nicolas acknowledges practical arithmetic as “very necessary in these Portuguese kingdoms and territories for the sake of the flourishing of the merchant trades of India and Persia and Arabia and Ethiopia and other major parts that have come to us”. Between 1472 and 1519, about forty books on arithmetic were published in Europe, including Luca Pacioli’s Summa, printed in Venice in 1494, which Gaspar Nicolas read and used in his own treatise.
Mathematics of Navigation, Sky Surveying and Cartography
Printing also played an important role in the development of the mathematical theory of navigation through the pioneering works of Pedro Nunes (1502–1578) [2 B. Almeida and H. Leitão, Pedro Nunes (1502–1578) mathematics, cosmography and nautical science in the 16th century, pedronunes.fc.ul.pt/index.html (2009) ]. It started with the edition in Portuguese of his Tratado da Sphera, printed in Lisbon in 1537 by Germão Galharde, the same typographer who typeset the Tratado da pratica Darismetyca. In two original chapters of that book, Nunes presented the first mathematical conceptualisation of the rhumb line, later called the loxodrome, as a new spherical spiral distinct from the great circles and illustrated by a polar projection with azimuth ±45º and ±67º 30’.
All rights reserved.
Subsequently this Portuguese mathematician suggested the rectification of the rhumb line for the maritime chart and developed original methods, in particular for the approximation of the rhumb line, which laid the foundations for the elaboration of nautical tables and the cartographic projection made in 1569 by Mercator in his famous mappa mundi [6 J. A. Gaspar and H. Leitão, How Mercator did it in 1569: from tables of rhumbs to a cartographic projection. Eur. Math. Soc. Newsl. 99, 44–49 (2016) ]. The broken line invented by Pedro Nunes to approximate the loxodrome was composed of small sections of great circles. It was first published in Latin in his Opera, in 1566 in Basel; it is now called the noniodrome and was chosen for the logo of the Leiria exhibition. It is the natural idea of approximating the loxodrome that corresponds to Euler’s modern method for integrating differential equations, and it was used numerically by Edward Wright in the secants’ method to construct nautical tables in 1596 [10 J. F. Rodrigues, The Nunes’ spiral and the prehistory of the infinitesimal calculus (in Portuguese). In 33rd Portuguese National Seminar on the History of Mathematics (October 2020), Boletim SPM (in press) ]. The re-edition in Coimbra of his Opera, in 1573, of Nunes’ fundamental work De arte atque ratione navigandi is a reference of Portuguese typography in the age when the scientific revolution started in the sixteenth century.
All rights reserved.
Practical and military use of mathematics before and after the Restoration
Printing was instrumental also in the teaching and practical use of mathematics for military architecture, navigation and artillery in Europe, and in particular in Portugal with the Methodo Lusitanico (1680) and O Engenheiro Portuguez (1728), both printed in Lisbon, after the Restoration of Portuguese independence in 1640 which ended the Iberian Union. Luís Serrão Pimentel (1613–1679), the posthumous author of the Methodo, was the Royal Cosmographer and Engineer who initiated the teaching and practices of military architecture in Portugal, in particular, using logarithms to solve trigonometry problems.
Mathematics book printing continued in Portugal for the navy and the army schools throughout the 18th and 19th centuries among others, with the Portuguese translations of the important book by Lagrange, La Théorie des fonctions analytiques being printed in Lisbon in 1798 just one year after its publication in Paris, and the two volumes of the Traité élémentaire du calcul différentiel et du calcul intégral by Lacroix at the Impressão Régia (Royal Printing House) in 1812 and 1814 respectively in Rio de Janeiro, which was the capital of the Portuguese kingdom from 1808 until 1821. Other original texts, such as the interesting Carta Físico-Mathematica sobre a theórica da pólvora em geral e o comprimento das peças em particular, written in 1769 by José Anastácio da Cunha and printed posthumously in Porto in 1838, show the important role played by the military in the history of mathematics in Portugal.
All rights reserved.
Teaching at the Colégio dos Nobres, Universidade and Colégio de São Lucas
Following the reforms of Marquis of Pombal, head of the government during the period of the Portuguese Enlightenment, the printing press would serve teaching with the publication of higher mathematics textbooks. These were initially translations of foreign authors, such as Euclid’s Elementos, printed in 1768, for the Colégio dos Nobres in Lisbon, several of Bézout’s textbooks for the first Faculty of Mathematics of the University of Coimbra, reformed in 1772, and in the following century, the Curso Completo de Mathematicas Puras (1838 and 1839) by Francoeur, which were printed at the University Press in Coimbra.
All rights reserved.
An exceptional book is the original and remarkable Princípios Mathematicos, the printing of which was completed in Lisbon only in 1790, by José Anastácio da Cunha (1744–1787), the military mathematician and “lente penitenciado”, a professor at the University of Coimbra from 1773 to 1778 who was then imprisoned by the Inquisition from 1978 to 1781. The Princípios, which was translated into French (Bordeaux, 1811) consisted of 21 chapters with 18 prints, and was intended to be the basis of all of mathematics, including geometry and arithmetic, algebra and series, differential and integral calculus. It also contains new and original theoretical contributions, such as the first rigorous definition of the convergence of a series, and the new concept of infinity and infinitesimal as variable quantities [5 A. J. Franco de Oliveira, Anastácio da Cunha and the concept of convergent series. Arch. Hist. Exact Sci. 39, 1–12 (1988) ], as well as a new theory of the exponential and logarithmic functions as convergent power series and the modern notion of differential, more than three decades before Cauchy, making J. A. da Cunha one of the eminent predecessors of the reform of infinitesimal calculus carried out in the 19th century [14 A. P. Youschkevitch, J. A. da Cunha et les fondements de l’analyse infinitésimale. Rev. Histoire Sci. Appl. 26, 3–22 (1973) , 15 A. P. Youschkevitch, C. F. Gauss et J. A. da Cunha, Rev. Histoire Sci. Appl. 31, 327–332 (1978) ].
Memoirs on the usefulness and on the foundations of mathematical sciences
The Lisbon Academy of Sciences, created in late 1779 and endowed with a printing press, began publishing its Memórias in 1797 with an article on applied mathematics, worthy of its motto “Nisi utile est quod facimus stulta est gloria” (If what we do is not useful, glory is in vain). Following the period of Regeneração in the 1850s which attempted to modernise the country and develop it economically, it continued with a new series that included some contributions to mathematics [11 L. M. R. Saraiva, Mathematics in the Memoirs of the Lisbon Academy of Sciences in the 19th century. Historia Math. 35, 302–326 (2008) ]. The new series included two memoirs by Daniel da Silva (1814–1878), in particular the remarkable On the rotation of forces around the points of application (1850, in Portuguese), which anticipated by a good quarter of a century a famous memoir by G. Darboux on the foundation of Statics.
All rights reserved.
The Academy also created the first Portuguese scientific journal, the Jornal de Sciencias Mathematicas Physicas e Naturaes (1866), which included a few mathematics articles, including an original article in Portuguese by Daniel da Silva on the amortisation of pensions in the main Portuguese survivors’ funds (1867), and another one devoted to a comparative study of the population in Portugal (1869).
All rights reserved.
Periodical publications with articles in the mathematical sciences
In 1853, the Coimbra University Press started publishing the scientific and literary periodical O Instituto, which included few mathematics articles mainly for didactic purposes. Although it was not a mathematical journal and did not contain any relevant mathematics research contributions, it did publish the interesting short but deep text Ensaio sobre os Princípios da Mechanica, written in the 1780s by J. A. da Cunha, in which he proposed a clear separation between the Physical and the Rational Mechanics, based on the axiomatic method.
The first Portuguese periodical exclusively dedicated to mathematics, the Jornal de Sciencias Mathematicas e Astronomicas by Francisco Gomes Teixeira (1851–1933), started publication in 1877 in Coimbra; it was printed at the University Press but it was independent of the University. It published fifteen volumes, and in addition to internationally promoting the mathematical activity of Portuguese mathematicians, it included international contributions, in particular by the French mathematician C. Hermite. Later its publication was transferred to Porto, and in 1905 it was integrated into the Annaes Scientificos da Academia Polytechnica do Porto. Only more than thirty years later did Portugal get a second mathematical journal, the Portugaliae Mathematica. However, following the Faculties of Science of the Universities of Porto, of Coimbra and of Lisbon, each of which created their own scientific journal containing some mathematical papers (in 1927, 1931 and 1937 respectively), in 1950 the Revista da Faculdade de Ciências de Lisboa started their 2nd series – A, exclusively dedicated to mathematics [8 J. F. Rodrigues, Portuguese mathematical journals: some aspects of (almost) periodical research publications. In The Practice of Mathematics in Portugal, edited by L. Saraiva and H. Leitão, Acta Univeritatis Conimbrigensis, Coimbra, 601–627 (2004) ]. It was directed by J. V. Gonçalves until 1966.
All rights reserved.
All rights reserved.
Higher mathematics textbooks in the transition from the 19th to the 20th century
The publication of original university textbooks by Portuguese authors would only continue a century later with the Curso de Analyse Infinitesimal by Francisco Gomes Teixeira, which was first published in 1887 in Porto. Written for the students of the Academia Polythecnica do Porto, it was later re-edited and expanded to become the reference Portuguese treatise of Mathematical Analysis at the beginning of the 20th century. It was later republished as Volumes III (1906) and VI (1912) of Teixeira’s Obras, published by the Coimbra University Press.
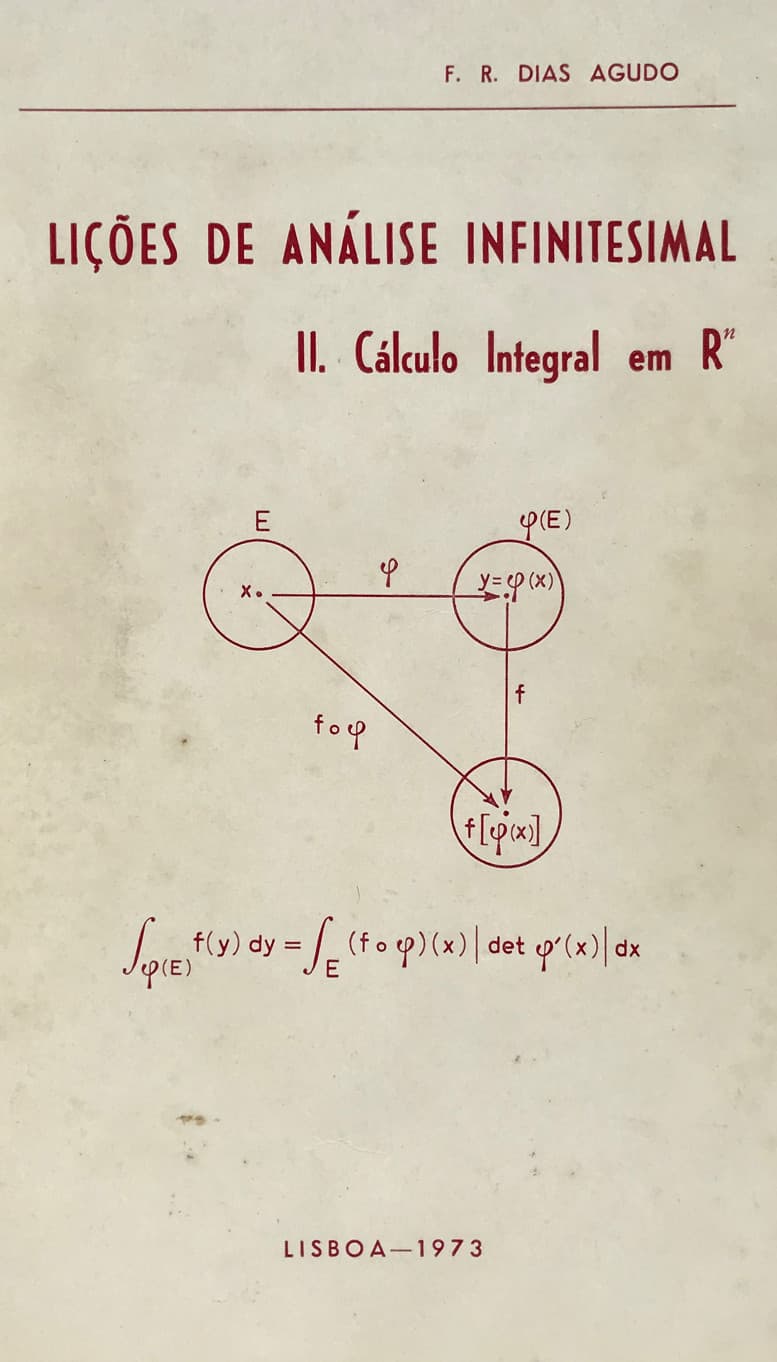
That university practice of writing textbooks had resumed only in the next century, examples being the classical Curso de Álgebra Superior by J. Vicente Gonçalves, whose first edition was printed in Coimbra, in 1933, and the modern Lições de Análise Infinitesimal by F. R. Dias Agudo, printed by the Tipografia Matemática in Lisbon in 1973 among several other textbooks.
Historical surveys, expository and popularisation books
Francisco Gomes Teixeira was the most active and prolific Iberian mathematician of the 19th century. He corresponded with numerous European mathematicians of his time, and was the first rector of the University of Porto, from 1911 to 1918. He was also the author of the remarkable and unsurpassed Traite des Courbes Spéciales Remarquables Planes et Gauches, which went through several editions and occupies three of the seven volumes of his Obras with a total of more than 1300 pages.
During the short decade 1937–1946, mathematical activity flourished in Portugal. For example, the remarkable little book Conceitos Fundamentais da Matemática, by Bento de Jesus Caraça (1901–1948), a Mathematics Professor at the Economics Institute in Lisbon who was expelled from the University in 1946 for political reasons, had a first edition in 1941. This was the first Portuguese book aimed at the popularisation of mathematics written in view of the “cultura integral do indivíduo” with a historical and materialistic philosophy.
All rights reserved.
Journals of the Portuguese Mathematics Society
The foundation of the scientific journal Portugaliae Mathematica in 1937 in Lisbon, by António Aniceto Monteiro (1902–1980), who had returned the year before from Paris where he had completed his doctoral degree under Maurice Fréchet, started a modernist movement also in Science with a certain “mathematical effervescence” that lasted for a short decade in Portugal [9 J. F. Rodrigues, António Monteiro and his modernist essay. CIM Bulletin 42, 3–10 (2020) ]. It was followed by the Gazeta de Matemática, in 1940, which was later printed by the Tipografia Matemática, and by the creation of the first research mathematical centre in the country, the Centro de Estudos Matemáticos de Lisboa, the same year. That unique typography was established in 1945 and had a remarkable, although limited, activity in the Portuguese mathematical press for more than three decades until 1977.
Finally, we mention some examples of research publications, such as the two doctoral theses printed at the Tipografia Matemática: the Publicação #18 of the Centro de Estudos Matemáticos do Porto, by A. Pereira Gomes (1919–2006), which was the first modern PhD thesis written in a Portuguese university, and As Funções Analíticas e a Análise Funcional, by José Sebastião e Silva (1914–1972), both published in Portugaliae Mathematica, respectively in 1946 and in 1950. In his work, J. Sebastião e Silva began work on some deep contributions to Functional Analysis, which would later lead him to introduce in 1955 an important class of locally convex spaces as inductive limits of an increasing sequence of normed spaces with compact inclusions [12 J. Sebastião e Silva, Su certe classi di spazi localmente convessi importanti per le applicazioni. Rend. Mat. e Appl. (5) 14, 388–410 (1955) ], later called the Silva LN*-spaces.
After five centuries of existence, the mathematical typography using movable type, with its specific and distinctive aspects such as tables, figures, diagrams and mathematical formulae, gave way to electronic publishing driven by the TeX program created by Donald Knuth in 1978 [7 D. E. Knuth, Mathematical typography. Bull. Amer. Math. Soc. (N.S.) 1, 337–372 (1979) ]. This electronic composition system was adopted by the American Mathematical Society five years later, and was used in 1987 by the Sociedade Portuguesa de Matemática (SPM) for the publication of the fiftieth anniversary volume 44 of Portugaliae Mathematica, which was chosen for the last book of the Leiria exhibition in order to complete this five-century-long retrospective of Portuguese mathematical typography, from 1496 until 1987.
References
- L. Albuquerque, Introdução, to the fac-simile edition of the Almanach Perpetuum. Imprensa Nacional-Casa da Moeda, Lisboa (1986)
- B. Almeida and H. Leitão, Pedro Nunes (1502–1578) mathematics, cosmography and nautical science in the 16th century, pedronunes.fc.ul.pt/index.html (2009)
- A. Alselmo, Origens da imprensa em Portugal. Imprensa Nacional-Casa da Moeda, Lisboa (1991)
- J. Chabàs and B. R. Goldstein, Astronomy in the Iberian Peninsula: Abraham Zacut and the transition from manuscript to print. Transactions of the American Philosophical Society 90.2, American Philosophical Society, Philadelphia, PA (2000)
- A. J. Franco de Oliveira, Anastácio da Cunha and the concept of convergent series. Arch. Hist. Exact Sci. 39, 1–12 (1988)
- J. A. Gaspar and H. Leitão, How Mercator did it in 1569: from tables of rhumbs to a cartographic projection. Eur. Math. Soc. Newsl. 99, 44–49 (2016)
- D. E. Knuth, Mathematical typography. Bull. Amer. Math. Soc. (N.S.) 1, 337–372 (1979)
- J. F. Rodrigues, Portuguese mathematical journals: some aspects of (almost) periodical research publications. In The Practice of Mathematics in Portugal, edited by L. Saraiva and H. Leitão, Acta Univeritatis Conimbrigensis, Coimbra, 601–627 (2004)
- J. F. Rodrigues, António Monteiro and his modernist essay. CIM Bulletin 42, 3–10 (2020)
- J. F. Rodrigues, The Nunes’ spiral and the prehistory of the infinitesimal calculus (in Portuguese). In 33rd Portuguese National Seminar on the History of Mathematics (October 2020), Boletim SPM (in press)
- L. M. R. Saraiva, Mathematics in the Memoirs of the Lisbon Academy of Sciences in the 19th century. Historia Math. 35, 302–326 (2008)
- J. Sebastião e Silva, Su certe classi di spazi localmente convessi importanti per le applicazioni. Rend. Mat. e Appl. (5) 14, 388–410 (1955)
- Tipografia Matemática Portuguesa: 1496–1987 – Catalogue (Portuguese), ipleiria.pt/sdoc/tipografia-matematica-portuguesa-1496-1987/
- A. P. Youschkevitch, J. A. da Cunha et les fondements de l’analyse infinitésimale. Rev. Histoire Sci. Appl. 26, 3–22 (1973)
- A. P. Youschkevitch, C. F. Gauss et J. A. da Cunha, Rev. Histoire Sci. Appl. 31, 327–332 (1978)
Cite this article
José Francisco Rodrigues, Portuguese mathematical typography: A brief overview from 1496 until 1987. Eur. Math. Soc. Mag. 123 (2022), pp. 17–24
DOI 10.4171/MAG/68