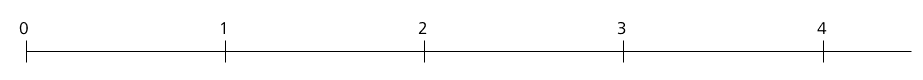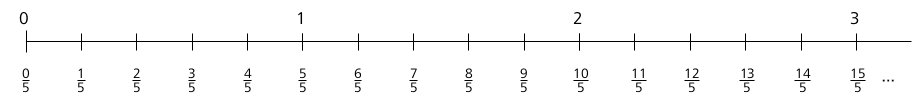Teaching school mathematics to prospective teachers

1 Introduction

Good school mathematics education requires teachers who are mathematically knowledgeable. After all, one can’t teach what one doesn’t know. However, at least in America, we are still none too sure about what kind of mathematics we should teach prospective teachers to make them knowledgeable (cf. [⁠12⁠ H. Wu, The content knowledge mathematics teachers need. In Mathematics Matters in Education, edited by Y. Li, W. J. Lewis and J. Madden, Springer, Cham, 43–91, https://math.berkeley.edu/~wu/Contentknowledge1A.pdf (2018) ]). In a well-known article back in 1990 [⁠1⁠ D. L. Ball, The mathematical understandings that prospective teachers bring to teacher education. Elementary School Journal90, 449–466 (1990) ], Deborah Ball reported on her study of the subject matter knowledge of 252 prospective mathematics teacher candidates (217 elementary school teachers and 35 high school teachers) in five universities. The study zeroed in on one topic: division of fractions. When presented with the division of $1\frac{3}{4}÷\frac{1}{2}$ and four story problems, only 30 % of them were able to select the problem that correctly represented this division. In a smaller study, 35 of the 217 teachers (25 elementary and 10 high school) were asked to create a word problem of their own to correctly represent this division. Only 4 out of the 35 teachers (thus 11 %) could give a satisfactory answer and all 4 were high school teachers. Ball’s (separate) interviews—on the same topic of fraction division—with mathematics majors in college who did not plan to go into teaching did not produce better results. Her conclusion was that the subject matter preparation of prospective teachers was in dire need of our serious reappraisal.

The inquiry into how best to help prospective teachers acquire the needed understanding of mathematics for teaching naturally predated Ball’s study and went back to at least the beginning of the 20th century. In the waning days of the New Math phase of the 1960s, E. G. Begle also pondered over the possible correlation between teachers’ knowledge of the subject matter and their students’ achievements. In his 1972 study of 308 teachers of high school algebra [⁠2⁠ E. G. Begle, Teacher knowledge and student achievement in algebra. SMSG Reports, No. 9, https://files.eric.ed.gov/fulltext/ED064175.pdf (1972) ], he found no evidence that the amount of teacher training in mathematics led to increased student achievement. This finding was further confirmed in 1979 [⁠3⁠ E. G. Begle, Critical Variables in Mathematics Education: Findings from a Survey of the Empirical Literature. Mathematical Association of America (1979) ].

The decades since the works of Begle and Ball have lent clarity to the phenomenon they uncovered. We will first analyze Ball’s data about $1\frac{3}{4}÷\frac{1}{2}$, and then put the data in the proper perspective by coming to terms with the fact that school mathematics is a separate discipline distinct from the mathematics we teach in universities.

2 The division of fractions: two views

We will approach the topic of fraction division from two perspectives. First, we describe what elementary students need to know to answer Deborah Ball’s questions and, second, what university students in a course on algebra can learn about fraction division. Due to length limitations, we will focus only on the critical mathematical differences between the two without addressing the pedagogical ramifications.

When the topic of fraction division is brought up in upper elementary school, students face a real conceptual challenge: the concept of a fraction is a higher level of abstraction than anything they have ever faced, and the concept of division is the most elusive of the four arithmetic operations on fractions. Students cannot overcome either obstacle if they are not told exactly what these concepts mean. As an Arizona elementary school teacher Kyle Kirkman said:

I have learned that precise mathematical definitions are critical. If precision is lacking, students will fill in any missing or vague elements of the definition with whatever happens to be present in their paradigm that seems to fit the idea. Not all of mathematics is intuitive in nature, so this can definitely lead to erroneous conclusions. [⁠12⁠ H. Wu, The content knowledge mathematics teachers need. In Mathematics Matters in Education, edited by Y. Li, W. J. Lewis and J. Madden, Springer, Cham, 43–91, https://math.berkeley.edu/~wu/Contentknowledge1A.pdf (2018) , Section 4.2.4]

Unfortunately, it is the case that school mathematics usually explains fractions to students in terms of vague metaphors without giving a precise definition, at least not one that students can use for reasoning about the four operations on fractions. We have to first describe a remedy for this deplorable situation. We will define a fraction in terms of something that feels “real” and “tangible” to elementary students, and the commonly accepted definition nowadays is as a point on the so-called number line (see [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) , Sections 12.1 and 12.2] or [⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , pp. 1–18]), as follows. We assume that we can tell whether two segments (i.e., closed intervals) on a line have equal length or not. A number line is a horizontal line on which the whole numbers have been identified as points so that the numbers $1,2,3,\dots$ are placed successively to the right of $0$ and the segments $[0,1],[1,2],[2,3],\dots$all have equal length (Figure ⁠1⁠). The fractions with denominators equal to $5$ (for example) consist of the whole numbers together with the division points when each of the segments $[0,1],[1,2],[2,3],\dots$ is divided into 5 equal parts, i.e., 5 segments of equal length (Figure ⁠2⁠). We call this sequence the sequence of fifths. We can likewise introduce the sequence of $n$-ths for each nonzero whole number $n$. (Observe the resemblance of the sequence of $n$-ths for each $n$ to the sequence of whole numbers.) Fractions are by definition the totality of all the points in the sequence of $n$-ths for all nonzero whole numbers $n$.

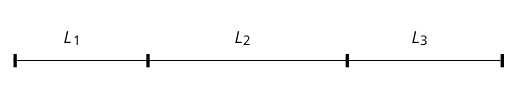
Next, we introduce the concept of length for certain segments. By definition, the length of the segment $[0,\frac{a}{b}]$ ($\frac{a}{b}$ a fraction) is $\frac{a}{b}$. Thus a segment with the same length as $[0,\frac{a}{b}]$ now also has length $\frac{a}{b}$. To put this definition to use, we introduce the concept of the concatenation of a collection of segments—say $L_1$, $L_2$, and $L_3$—to be the segment formed by putting these segments together end-to-end:

It follows that the length of the concatenation of 3 of the parts when $[0,1]$ is divided into (let us say) 7 equal parts is $\frac{3}{7}$ because this segment has the same length as $[0,\frac{3}{7}]$.

Since division is based on multiplication, we will come straight to fraction multiplication without discussing equivalent fractions or fraction addition. By definition, $\frac{2}{5}\times \frac{3}{4}$ is the length of the concatenation of 2 of the parts when the segment $[0,\frac{3}{4}]$ is divided into 5 equal parts. The multiplication of two fractions in general is defined similarly (see, e.g., [⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , Section 1.5] or [⁠15⁠ H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020) , Section 1.4]). It becomes a nontrivial fact (for elementary students) to prove the following product formula:

See, e.g., [⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , Theorem 1.5, p. 60].

This definition of fraction multiplication did not come out of the blue. If, in the definition of $\frac{2}{5}\times \frac{3}{4}$, we replace the fraction $\frac{3}{4}$ by $1$ ($=\frac{1}{1}$), then the definition of $\frac{2}{5}\times 1$ (“the total length of 2 of the parts when $[0,1]$ is divided into 5 equal parts”) becomes exactly the above definition of $\frac{2}{5}$, so that (not surprisingly) $\frac{2}{5}\times 1=\frac{2}{5}$. Furthermore, if we consider the product of whole numbers, say $2\times 3$, we can also regard it as the multiplication of the fractions $\frac{2}{1}$ and $\frac{3}{1}$. Then the definition of fraction multiplication says that this product is the total length of 2 of the parts when the segment $[0,3]$ is divided into 1 equal part, i.e., when each part is the segment $[0,3]$ itself. In other words, the product $2\times 3$, whether considered as the product of two whole numbers or the product of two fractions, is just $3+3$. In this light, we see that this definition of fraction multiplication is a very natural outgrowth of familiar concepts.

How is this concept of multiplication related to the real world? To elementary students, this is an important concern, as the following problem shows.

Incidentally, this explains why, when textbooks do not define fraction multiplication, they give the rote instruction that the word “of” means “multiply”.

Next, division. We must first review the concept of division among whole numbers (see [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) , pp. 97–100]). Observe that, whereas we can add or multiply any two whole numbers, we are not free to subtract or divide any two whole numbers. For example, in the context of whole numbers, the subtraction $3-7$ is not allowed, nor is $21÷5$. Let us explain the latter: within whole numbers, we can write $21÷7$ (respectively, $15÷3$) only because we know ahead of time that 21 (resp. 15) is a whole number multiple of 7 (resp. 3). For example, the definition of division $21÷7$ is:

This is why $21÷7=3$. The definition makes it perfectly clear that, without a prior guarantee that 21 is a multiple of 7, the whole number$21÷7$ would be impossible to define. Equivalently, if we do not know that 21 objects can be partitioned into 3 equal groups of 7, then we cannot talk about $21÷7$. If students find equation (⁠2⁠) to be confusing, remind them that (⁠2⁠) is no different from the definition of subtraction:

Why this review is important is that the division among whole numbers serves as a model for the division among fractions, because whole numbers are also fractions (see [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) , pp. 284–289]). So, according to (⁠2⁠), the division $1\frac{3}{4}÷\frac{1}{2}$ ($1\frac{3}{4}$ is just $\frac{7}{4}$) would make no sense unless $1\frac{3}{4}$ is a fractional multiple of $\frac{1}{2}$ in the sense that $1\frac{3}{4}=\frac{m}{n}\times \frac{1}{2}$ for some fraction $\frac{m}{n}$. (This $\frac{m}{n}$ is unique; see [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) , Lemma, p. 286] or [⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , Lemma 1.7, p. 75].) Assuming there is such an $\frac{m}{n}$, then we can define $1\frac{3}{4}÷\frac{1}{2}$ in exactly the same way as in (⁠2⁠):

See [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) , p. 289] or [⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , p. 75].

Surprisingly, in contrast with the case of whole numbers, it turns out that such a fraction $\frac{m}{n}$ on the right side of (⁠3⁠) can always be found as follows:

From (⁠4⁠), we see that if we let $\frac{m}{n}=\frac{2}{1}\times 1\frac{3}{4}$, then $1\frac{3}{4}=\frac{m}{n}\times \frac{1}{2}$ and (⁠3⁠) would allow us to conclude that

This is of course the invert and multiply rule for fraction division. This reasoning is seen to be perfectly general.

We now give a word problem whose solution requires the use of the division $1\frac{3}{4}÷\frac{1}{2}$ in Ball’s article [⁠1⁠ D. L. Ball, The mathematical understandings that prospective teachers bring to teacher education. Elementary School Journal90, 449–466 (1990) ] and we will also explain how this comes about.

We have now done enough to show the minimal mathematical knowledge a school teacher needs to teach fraction division correctly to elementary students. We point out once again that this minimal knowledge is not typically what elementary students are taught in schools. Be that as it may, it is time to take up the other concern in Ball’s 1990 article about why university mathematics majors may not possess such knowledge either. We will only be able to provide the barest outline in the following discussion.

A university course on abstract algebra that includes the mathematically correct way to define fractions is essentially students’ first introduction to abstract mathematics. The main purpose of such a course is to guide students’ first steps in the new environment of what is called abstract mathematics. Hence the relentless emphasis in such courses is on correct definitions and proofs, and on reducing all complex mathematical phenomena—by the use of logic—down to the bare essentials. For the case at hand, let us put ourselves at the juncture where students are already in possession of the integers, to be denoted by $\mathbb{Z}$, and are made aware that the main defect of $\mathbb{Z}$ from an abstract point of view is that no nonzero integer other than $1$ and $-1$ has a multiplicative inverse, i.e., given an integer $z$, $z\ne 1$ or $-1$, there is no integer $z^{\prime }$ so that $z{z}^{\prime }=z^{\prime }z=1$. The way to eliminate this defect is to expand $\mathbb{Z}$ by including the desired multiplicative inverses to form the field of quotients$\mathbb{Q}$. This $\mathbb{Q}$ is of course what we call the rational numbers (the fractions and negative fractions), but in the abstract setting, we cannot just adjoin the new numbers $\pm \frac{1}{2}$, $\pm \frac{1}{3}$, etc., to $\mathbb{Z}$ and declare, “There you are!”. After all, what are these new numbers and how do we add and multiply them? We want students to learn how to use a similar reasoning to expand any integral domain into a field so that every nonzero element of the integral domain will have a multiplicative inverse in the field. The way to do this is to form the set of all ordered pairs of integers $\{⟨u,v⟩\}$ (where $u$ and $v$ are integers with $v\ne 0$) and introduce into this set an equivalence relation (which essentially declares that the cross-multiplication algorithm is valid), and then $\mathbb{Q}$ is by definition the set of equivalence classes. After that, we can show that each integer $u$ in $\mathbb{Z}$ can be identified with the equivalence class containing $⟨u,1⟩$, and we also write $\frac{u}{v}$ for the equivalence class containing $⟨u,v⟩$ so as to align the new notation with the old. In particular, this means $\frac{u}{1}$ is identified with the integer $u$ for each $u$.

For beginners, just getting used to this general construction and being at ease with the idea that each “number” in $\mathbb{Q}$ is now an equivalence class (each containing an infinite number of elements) is already a full-time job. But more is yet to come. So far, we only have a larger set $\mathbb{Q}$ containing $\mathbb{Z}$ but we do not yet know how to do arithmetic in $\mathbb{Q}$, i.e., given two arbitrary elements of $\mathbb{Q}$, we do not know as yet how to add them or multiply them. The next step is therefore to define the rules for adding and multiplying elements in $\mathbb{Q}$ (which are equivalence classes) with the goal of showing that $\mathbb{Q}$ in fact forms a field, which means in particular that each nonzero element $z$ of $\mathbb{Q}$ will have a multiplicative inverse $z^{-1}$, i.e., so that $z{z}^{-1}=z^{-1}z=1$. Here are the relevant definitions: for $u$, $v$, $s$, $t$ in $\mathbb{Z}$ with $v\ne 0$ and $t\ne 0$,

We underscore the momentous shift in perspective that has just taken place here. In school mathematics, fractions are considered to be a part of nature that students should get to know; the idea that two fractions can be multiplied is taken for granted. What needs to be to explained is how the product of two fractions is related to the daily phenomena around us and why the product formula (⁠1⁠) is correct. By contrast, abstract mathematics progresses from $\mathbb{Z}$ to $\mathbb{Q}$ by regarding only the integers as known so that how to add or multiply the unknown non-integer rational numbers is a total blank that is waiting to be filled in; this is done by judiciously defining what the sum and product of two rational numbers must be. The internal structure of $\mathbb{Q}$ is the sole concern here, not how $\frac{u}{v}\times \frac{s}{t}$ is related to daily phenomena. In particular, whereas equation (⁠1⁠) is a theorem in school mathematics, the same statement (⁠5⁠) is merely a definition in university mathematics.

We can now explain why university mathematics majors are generally not capable of explaining to elementary students how to multiply two fractions. First of all, most if not all of these math majors were not provided with this kind of knowledge when they were in elementary school themselves (see, e.g., [⁠16⁠ H. Wu, Learnable and unlearnable school mathematics. https://math.berkeley.edu/~wu/AE2020A.pdf (2021) ]). More to the point, what they learn about fractions in college mathematics courses is about the abstract structure of the rational numbers as a field, not about how fractions are related to daily experiences. Therefore, it is not that university mathematics majors are ignorant about fractions, but that their understanding of fractions is divorced from the concerns of elementary students. To the extent that multiplication is the foundation of division, the same comment will apply to the school mathematics of fraction division, as we now show.

As part of the mission of university mathematics to reduce all phenomena to bare essentials, the four arithmetic operations in school mathematics are reduced to only two, namely, addition and multiplication. In a field, subtraction $a-b$ is by definition the addition $a+(-b)$, where $-b$ is the additive inverse of $b$, and division $a÷b$ ($b\ne 0$) is by definition just the multiplication $a\times b^{-1}$, where $b^{-1}$ is the multiplicative inverse of $b$. Since the multiplicative inverse of a nonzero rational number $\frac{s}{t}$ is clearly just the reciprocal $\frac{t}{s}$, the invert-and-multiply rule is now—like the product formula (⁠5⁠)—a matter of definition:

From the point of view of abstract mathematics, “division” is just an afterthought once multiplication is in place. Mathematics majors would usually be busy with exploring the new algebraic structures (groups, fields, rings, etc.) at this point and any puzzlement over division or its ramifications in real life simply does not enter the picture. If they cannot help elementary students overcome the fear of “Ours is not to reason why, just invert and multiply”, it is—again—not because they know less than school teachers but because they know something different from the concerns of elementary students.

3 What is school mathematics?

Through one small topic—fraction division—we get to see the critical difference between what may be called university mathematics (the mathematics taught in universities to prepare students for mathematical research) and school mathematics (the mathematics taught in K-12 schools). A main goal of the former is to introduce students to abstract mathematics, and the main emphasis is on logical completeness and the use of abstractions to achieve this goal. No matter how gently this is done, it is too austere and too sophisticated to be suitable for use in schools. School students who come mostly from the world of tactile experiences need a bridge to help them transition to the world of abstractions. School mathematics is that bridge, and it should be recognized as an independent discipline devoted to the customization of university mathematics to meet the needs of school students, in the same way that chemical engineering is the discipline that customizes abstract chemical principles to meet human needs. In this sense, school mathematics is mathematical engineering (see [⁠7⁠ H. Wu, How mathematicians can contribute to K-12 mathematics education. In Proceedings of International Congress of Mathematicians, Vol. III (Madrid, 2006), European Mathematical Society, 1676–1688, http://math.berkeley.edu/~wu/ICMtalk.pdf (2006) ]).

Now, there is good engineering and there is also bad engineering. Good engineering always observes the basic principles of its associated scientific discipline—for example, mechanical engineering does not engage in designing perpetual motion machines—but bad engineering can do just the opposite. In the case of mathematics, bad mathematical engineering has been at work for a long time at least in America; it has produced school mathematics that seems to make a mockery of the fundamental principles of mathematics (see, e.g., [⁠16⁠ H. Wu, Learnable and unlearnable school mathematics. https://math.berkeley.edu/~wu/AE2020A.pdf (2021) ]). But before proceeding any further, let us state one version of the fundamental principles of mathematics [⁠8⁠ H. Wu, Phoenix rising. Bringing the Common Core State Mathematics Standards to life. Amer. Educator35, 3–13, www.aft.org/pdfs/americaneducator/fall2011/Wu.pdf (2011) ]:

1. Clear definitions. Each concept is precisely defined so as to be usable for reasoning.

2. Logical reasoning. Every claim is supported by reasoning that explains why it is true. (It is understood that in a few special cases, such as the fundamental theorem of algebra, the reasoning can be deferred.)

3. Precise language. There is no place for ambiguity in a discipline where the difference between true and false is absolute.

4. Coherence. The concepts and skills are not fragmented bits and pieces but are part of a coherent whole.

5. Purposefulness. Each concept or skill is there for a purpose.

We have seen all of them in action in the preceding discussion of fraction division. Thus, fraction, fraction multiplication, and fraction division were all precisely defined to make possible the use of reasoning to explain formulas (⁠5⁠) and (⁠6⁠). An example of the precision that is in school mathematics is the definition of division among whole numbers that shows why “$m÷n$” does not always make sense for two arbitrary whole numbers $m$ and $n$. As for “coherence”, we took pains to explain how the definition of fraction multiplication evolves from the definition of a fraction as well as from the definition of whole-number multiplication. We also showed that the definition of fraction division is modeled on the definition of whole-number division. Finally, although the purpose of the concepts of fraction multiplication and division is all too obvious, there are many other concepts or skills whose presence in the school curriculum is not well explained, e.g., why learn how to round to the nearest ten or nearest thousand (see [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) , Chapter 10]), why take the absolute value of a real number (see [⁠15⁠ H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020) , pp. 130–131] and [⁠14⁠ H. Wu, Pre-Calculus, Calculus, and Beyond. American Mathematical Society, Providence (2020) , pp. 120, 123]), etc. Also see the discussion of slope below.

We will refer to school mathematics that observes the fundamental principles of mathematics as PBSM (Principles-Based School Mathematics; see [⁠5⁠ R. C. Poon, Principle-based mathematics: an exploratory study. Dissertation at University of California, Berkeley, http://escholarship.org/uc/item/4vk017nt (2014) ]).

We now have the necessary tools to revisit the problem concerning the mathematical education of teachers that Begle, Ball, and others uncovered but did not clearly articulate. In our language, their message is that to get mathematically knowledgeable teachers, we have to teach teachers PBSM instead of university mathematics. This is because school mathematics and university mathematics are related but essentially distinct disciplines, so that knowing university mathematics does not imply knowing PBSM. We have underscored their differences using a small topic—that of fraction division—but there are many other such examples. Let us briefly look at two additional ones to further plead our case: the concept of the slope of a line, and the broad issue of the school geometry curriculum. Similar examples are pointed out throughout the six volumes [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) , ⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , ⁠10⁠ H. Wu, Teaching School Mathematics: Algebra. American Mathematical Society, Providence (2016) , ⁠15⁠ H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020) , ⁠13⁠ H. Wu, Algebra and Geometry. American Mathematical Society, Providence (2020) , ⁠14⁠ H. Wu, Pre-Calculus, Calculus, and Beyond. American Mathematical Society, Providence (2020) ].

First, consider how school mathematics handles “slope”. The typical starting point is to let students retain their naive conception of a line as in Euclidean geometry and define slope in terms of this naive conception. Thus, let a line $L$ in the coordinate plane ${\mathbb{R}}^2$ be given. Suppose $L$ is not vertical (i.e., not parallel to the $y$-axis). Then school mathematics defines the slope of $L$ as the quotient

where $(x_1,y_1)$ and $(x_2,y_2)$ are any two distinct points on $L$.

We can explain to students that the slope of a (nonvertical) line is a measurement of its “slant” relative to the $y$-axis (see [⁠15⁠ H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020) , pp. 338–346]). Incidentally, this explanation is an example of the purposefulness of a concept. In any case, the central fact concerning slope is the following theorem [⁠14⁠ H. Wu, Pre-Calculus, Calculus, and Beyond. American Mathematical Society, Providence (2020) , Theorem 6.11, p. 354].

There is a subtlety hidden in the definition of slope: how do we know that the right side of (⁠7⁠) does not change no matter which two points $(x_1,y_1)$ and $(x_2,y_2)$ are chosen on $L$? Most school textbooks evade this question, leading to much confusion in students’ understanding of slope. The fact is that to answer this question, we need the theorem that two triangles are similar if they have a pair of equal angles. Rare is the school curriculum that has covered similar triangles by the time it takes up the topic of slope. Consequently, slope is rarely defined correctly. If there is no correct definition for a concept, then there can be no theorem involving the concept. Consequently, Theorem ⁠1⁠ is almost never proved in school mathematics.

Not surprisingly, university mathematics approaches slope by ignoring any reference to students’ naive knowledge and simply defining a line in the plane as the graph of an equation $y=mx+b$ ($m$ and $b$ being constants) or $x=b$ (a vertical line). Then the slope of the graph of $y=mx+b$ is by definition $m$. Very simple! Therefore, brevity and total clarity are achieved at the expense of students’ intuition. (Unfortunately, there are mathematics textbooks for teachers that ignore the need for mathematical engineering and also define a line the same way.) Clearly, such an understanding of the slope of a line, while mathematically correct, will not help secondary school students to come to terms with the concept of slope.

Finally, a few passing remarks about the school geometry curriculum. There are obvious defects in this curriculum that cry out for correction. We have already brought up the need for coordinating the teaching of similar triangles with the teaching of slope; this need is generally not met. There is also the need to explain the concepts of congruence and similarity because they come up naturally in daily life. However, the school curriculum usually teaches only triangle congruence and similarity in the course on Euclidean geometry but never the congruence and similarity of general geometric figures. This is not only defective as general education but also detrimental to the school mathematics curriculum itself as a general knowledge of the congruence and similarity of parabolas would greatly clarify the subject of quadratic equations and functions (see [⁠13⁠ H. Wu, Algebra and Geometry. American Mathematical Society, Providence (2020) , Sections 2.1 and 2.2]). Last but not least, the course on Euclidean geometry is usually flaunted as the crown jewel of school education on teaching students how to use logic to prove everything strictly on the basis of axioms. The sooner we can disabuse school students of this illusion the better! Indeed, we have known since the work of Hilbert (1862–1943) that the axiomatic system of Euclidean geometry is extraordinarily subtle and its inner workings are not suitable for the education of school students (see the early chapters in Hartshorne’s book [⁠4⁠ R. Hartshorne, Geometry: Euclid and Beyond. Springer (1997) ]; they will tax the dedication of even university mathematics majors). School mathematics education should steer away from this make-believe about axiomatic systems of Euclidean geometry and, instead, try to introduce a reasonably large number of redundant assumptions into Euclidean geometry to minimize students’ need to prove many boring, obvious, and difficult-to-prove theorems at the beginning. Compare [⁠15⁠ H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020) , Chapters 4–5] and [⁠13⁠ H. Wu, Algebra and Geometry. American Mathematical Society, Providence (2020) , Chapters 6–8].

Needless to say, no part of university mathematics will ever address any of these issues in the presentation of high school geometry. Serious mathematical engineering is called for here to make plane geometry truly consumable by high school students.

4 An existence proof

Thus far, we have advocated for the need to teach prospective teachers PBSM. The implicit assumption is that PBSM has always been around and is ready for the taking. This is a pleasant assumption to make and an even more pleasant assumption to believe. However, it is sobering to realize that, with all kinds of defective school mathematics out in the world, there is a distinct possibility that university mathematics can never be customized for the consumption of school students without violating one or more of the fundamental principles of mathematics. Alan Schoenfeld seems to be the first among educators to acknowledge in 1994 that, although he believed that something like PBSM should exist, there was as yet no documented proof that such was the case [⁠6⁠ A. Schoenfeld, What do we know about Mathematics Curricula? J. Math. Behavior13, 55–80 (1994) ]. What we can report in 2021 is that there is now at least one systematic exposition of PBSM from kindergarten to grade 12 in the form of six volumes: [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) ] for teachers of grades K-5, [⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , ⁠10⁠ H. Wu, Teaching School Mathematics: Algebra. American Mathematical Society, Providence (2016) ] for teachers of grades 6–8, and [⁠15⁠ H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020) , ⁠13⁠ H. Wu, Algebra and Geometry. American Mathematical Society, Providence (2020) , ⁠14⁠ H. Wu, Pre-Calculus, Calculus, and Beyond. American Mathematical Society, Providence (2020) ] for teachers of grades 9–12.

We can explain the need for such a complete exposition of thirteen years of PBSM. There have been articles and books that demonstrate the possibility of introducing reasoning to a specific topic or two in school mathematics, but discussions on such a small scale cannot bring out the essence of the fundamental principles of mathematics. For example, to expose teachers to the need for precise definitions, we cannot show them PBSM on just a few key topics because teachers need to experience this need in every aspect of school mathematics, including the definitions of the most mundane of concepts such as percent, ratio, speed, equation, variable, angle, graph of an inequality, etc. Or, consider the issue of coherence: it is usually invisible when school mathematics is viewed through a microscope, such as a focus on fraction addition or fraction division. But when the subject of fractions is taken as a whole, then the way the theorem of equivalent fractions pulls all the diverse parts of fractions together becomes somewhat breathtaking (see, e.g., [⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , pp. 28–86]). On a slightly larger scale, one also gets to witness coherence at work when the concept of division is shown to be qualitatively the same for whole numbers, fractions, rational numbers, and real numbers (cf. [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) ]). We should add that, without such a longitudinal overview of school mathematics, the defects of the school geometry curriculum might not have been detected.

The 6-volume exposition of PBSM, beyond providing a foundation for student textbooks in school mathematics, shows in detail how we can achieve a better mathematical education for teachers. In America, teachers are taught in three grade-bands: elementary (K-grade 5), middle school (grades 6–8), and high school (grades 9–12). As noted above, the six volumes in question have been written with these grade-bands in mind so that, collectively, they now provide one answer to the original question implicitly raised by Begle, Ball, et al., namely, what kind of mathematics should we teach teachers? (A more detailed answer to this question is given in [⁠15⁠ H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020) , p. xxi].) It goes without saying that school mathematics curricula are not now—and won’t ever be—all alike, but we hope such a complete exposition of PBSM will nevertheless contribute to better school mathematics education by freeing educators from the need to perform the necessary mathematical engineering. It should now be relatively easy to freely modify this existing model [⁠9⁠ H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011) , ⁠11⁠ H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016) , ⁠10⁠ H. Wu, Teaching School Mathematics: Algebra. American Mathematical Society, Providence (2016) , ⁠15⁠ H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020) , ⁠13⁠ H. Wu, Algebra and Geometry. American Mathematical Society, Providence (2020) , ⁠14⁠ H. Wu, Pre-Calculus, Calculus, and Beyond. American Mathematical Society, Providence (2020) ] to meet diverse needs.

Acknowledgements I am very indebted to Larry Francis for his important suggestions for improvement.

Hung-Hsi Wu is Professor Emeritus of Mathematics at the University of California at Berkeley, U.S.A. He is a geometer but has spent the last twenty-five years educating school teachers. wu@berkeley.edu

References

1. D. L. Ball, The mathematical understandings that prospective teachers bring to teacher education. Elementary School Journal90, 449–466 (1990)
2. E. G. Begle, Teacher knowledge and student achievement in algebra. SMSG Reports, No. 9, https://files.eric.ed.gov/fulltext/ED064175.pdf (1972)
3. E. G. Begle, Critical Variables in Mathematics Education: Findings from a Survey of the Empirical Literature. Mathematical Association of America (1979)
4. R. Hartshorne, Geometry: Euclid and Beyond. Springer (1997)
5. R. C. Poon, Principle-based mathematics: an exploratory study. Dissertation at University of California, Berkeley, http://escholarship.org/uc/item/4vk017nt (2014)
6. A. Schoenfeld, What do we know about Mathematics Curricula? J. Math. Behavior13, 55–80 (1994)
7. H. Wu, How mathematicians can contribute to K-12 mathematics education. In Proceedings of International Congress of Mathematicians, Vol. III (Madrid, 2006), European Mathematical Society, 1676–1688, http://math.berkeley.edu/~wu/ICMtalk.pdf (2006)
8. H. Wu, Phoenix rising. Bringing the Common Core State Mathematics Standards to life. Amer. Educator35, 3–13, www.aft.org/pdfs/americaneducator/fall2011/Wu.pdf (2011)
9. H. Wu, Understanding Numbers in Elementary School Mathematics. American Mathematical Society, Providence (2011)
10. H. Wu, Teaching School Mathematics: Algebra. American Mathematical Society, Providence (2016)
11. H. Wu, Teaching School Mathematics: Pre-Algebra. American Mathematical Society, Providence (2016)
12. H. Wu, The content knowledge mathematics teachers need. In Mathematics Matters in Education, edited by Y. Li, W. J. Lewis and J. Madden, Springer, Cham, 43–91, https://math.berkeley.edu/~wu/Contentknowledge1A.pdf (2018)
13. H. Wu, Algebra and Geometry. American Mathematical Society, Providence (2020)
14. H. Wu, Pre-Calculus, Calculus, and Beyond. American Mathematical Society, Providence (2020)
15. H. Wu, Rational Numbers to Linear Equations. American Mathematical Society, Providence (2020)
16. H. Wu, Learnable and unlearnable school mathematics. https://math.berkeley.edu/~wu/AE2020A.pdf (2021)