To an outside observer, I suppose I appear to be working on the history of mathematics in ancient and medieval China. To a certain extent, this is true. However, this is also partly wrong. By this (perhaps unexpected) statement, I do not mean simply that I have also carried out research and published on the history of projective geometry and of duality more broadly, as well as on the history of medieval mathematics in Arabic, Greek, Hebrew and Sanskrit. I mean something deeper. Working on the history of mathematics in China is certainly meaningful in and of itself. However, to my eyes, it becomes all the more meaningful in that it confronts us with sources with which we are not used to thinking about mathematics, and these sources suggest interesting new issues, as well as new ways of addressing old issues. In other words, Chinese sources, like in fact any mathematical document if treated appropriately, give us resources with which to nurture a theoretical approach to the history of mathematics. This, in the end, is my main goal. In what follows, I will illustrate how this has worked for me in practice, by discussing some of the theoretical issues I have been led to address in the course of my research.
1 History of science, history of text
My first significant encounter with Chinese mathematical sources took place in 1981, as I was studying in China at the Institute for the History of Natural Sciences (Chinese Academy of Sciences), and it confronted me right away with striking phenomena, about which I still think today.
Following a suggestion that had been made to me by Leuven sinologist Ulrich Libbrecht, I started reading the book that Li Ye 李冶 (1192–1279) had published in 1248 under the title Measuring the Circle on the Sea-Mirror (Ceyuan haijing 測圓海景, hereafter Measuring the Circle), which was to become the subject of my dissertation. For this, I benefited from the guidance of the person in charge of organizing my study in Beijing at the time, Mei Rongzhao 梅榮照, who had already worked on Li Ye’s book. I was also lucky to receive advice from the group of scholars who had been appointed to teach me during my time in China, namely: Du Shiran 杜石然, Guo Shuchun 郭書春, He Shaogeng 何紹庚 and Yan Dunjie 嚴敦傑.
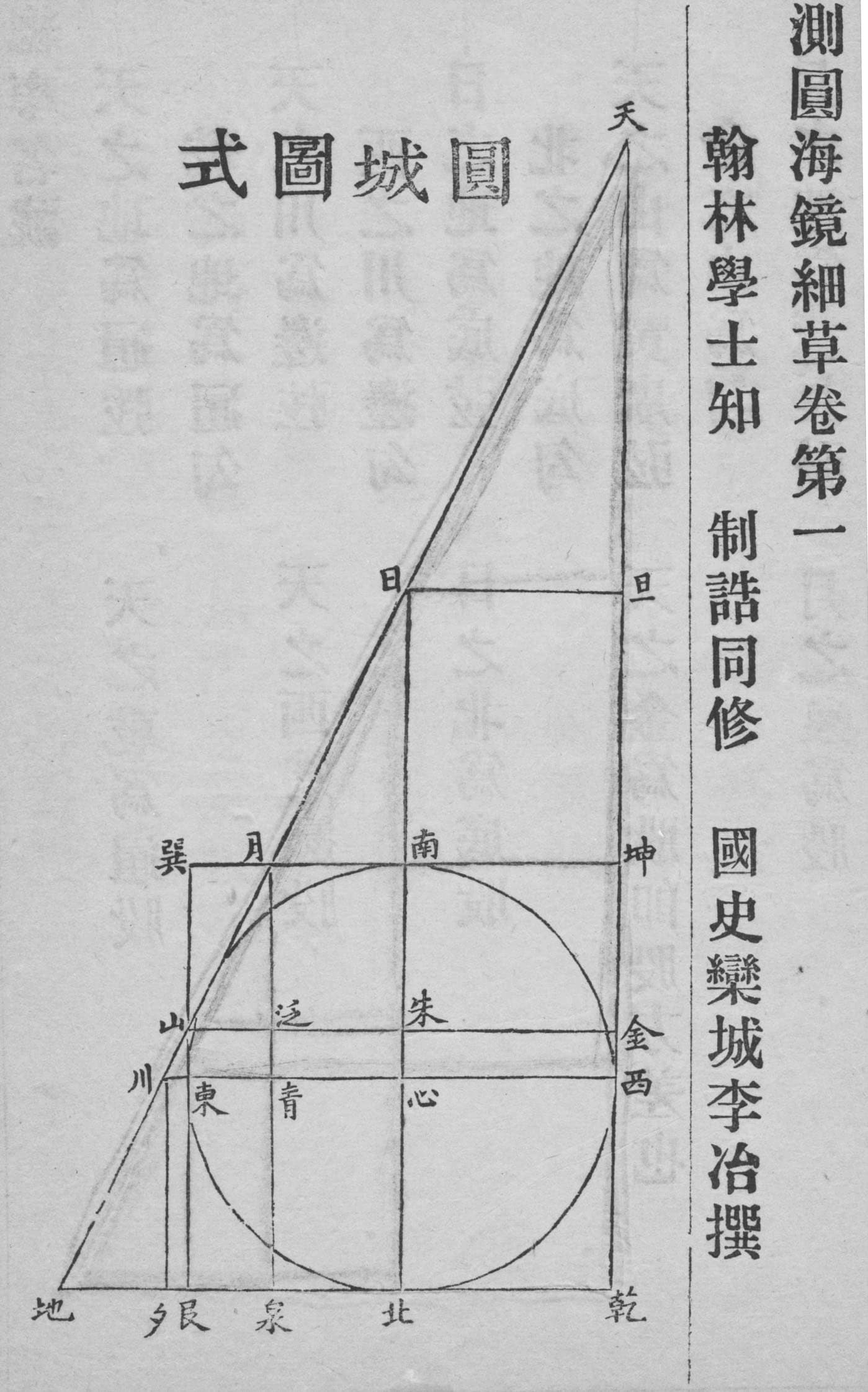
Li Ye’s book opens with a diagram, to which the entire book is devoted (see Figure 2, and Chemla [7 K. Chemla, Une figure peut en cacher une autre. Reconstituer une pratique des figures géométriques dans la Chine du XIIIe siècle. Images des mathématiques, images.math.cnrs.fr/Une-figure-peut-en-cacher-une.html (2011) ] for an analysis). The diagram is followed by a set of about 700 formulas, stating relationships between its segments, and then 170 problems, which basically all share the same structure. They give two segments of the diagram and in general ask to determine the diameter of the circle. The point of the problems is thus not the answer, since it is systematically the same, but rather the method. Li Ye begins with the choice of an unknown (not always the diameter itself, but a magnitude that could easily be related to it), to which he refers as “the celestial origin”. He then brings into play polynomials, written using a place-value notation, along with a geometrical reasoning that relies on the data and the unknown, in order to establish an algebraic equation, “the” root of which is the unknown sought (see Figure 1). Indeed, at the time, in China, equations were considered as having a single root. In brief, this was how the book had been understood up to then: it was the earliest extant book attesting to the algebraic method known as “the procedure of the celestial origin tian yuan shu 天元術.”
However, something immediately struck me in the solutions Li Ye gave to the problems. Every solution had the same structure, which consisted of two parts. Each of these parts described, in a different way, how to obtain the same equation that solved the problem. The first part, called “method” (fa 法), described a sequence of algorithms that relied on the data to compute the successive coefficients of the sought-for equation. In this part, there were no numerical values, in contrast with the second part, called “detail of the procedure” (cao 草), which, starting from the data and the chosen unknown, presented two ways of reasoning to obtain the same geometrical magnitude and a numerical polynomial associated with it. The reasonings, along with the related polynomial computations, systematically followed the same pattern: each step consisted of an operation that took previously determined magnitudes and the associated polynomial as its operands, and then yielded a result in the form of another magnitude (the reasoning part) and the polynomial associated with it (the computation part). At the end of a procedure of this kind, the equation was obtained numerically, by subtracting from each other the two polynomials that corresponded to the same magnitude. Why, I wondered, should the author systematically tell the reader, twice and in two different ways, how to get the same equation? This was my first question, soon followed by a second one: taking for granted that the “method” and the “detail of the procedure” led to exactly the same equation, how were the algorithms given in the “method” obtained?
For each of the 170 problems, I made an experiment. I computed the sequences of polynomials leading to the final equation in the “details of the procedure” symbolically, and not numerically as they were presented in Li Ye’s book. Although the text did not contain any computation of this kind, I established that, in each case, my computations highlighted a missing link between the algorithms of the “method” and the “details of the procedure”. Indeed, every algorithm in the “method” actually described the sequence of operations that, in the symbolic computations deriving from the “details of the procedure”, had been applied to coefficients of successive polynomials to shape the corresponding coefficient of the final equation [2 K. Chemla, Equations with general coefficients in the Ce Yuan Hai Jing. Publications de l’Institut de Recherche Mathématique de Rennes, Fascicule II: Science, Histoire, Société, 23–30, www.numdam.org/article/PSMIR_1985___2_23_0.pdf (1985) ]. In brief, using mathematical knowledge and practice that did not feature in the book, and that appeared long after the book was completed (that is, algebraic symbolism and algebraic computations), I could highlight a correlation between the two parts of every solution. The correlation was so intimate that the “method” could not have been obtained independently from the “details of the procedure”. Clearly, the systematic correlation yielded a clue indicating that the description in the “method” derived from a work that Li Ye had carried out, but not recorded in his book. So the question became: what kind of mathematical work was that?
Perhaps, in the future, someone will find clues in Measuring the Circle, or elsewhere, to answer this question with certainty. However, as far as we know today, nothing in the book seems to indicate exactly how, for every single problem, Li Ye produced the “method” part of the solution, relying on the “details of the procedure” part. I cannot attribute to him without further ado the knowledge that I, as an observer, bring into play to establish the correlation between the “method” and the “details of the procedure”. Nevertheless, my experiment sheds light on knowledge that Li Ye must have possessed, and practices that he must have used, in order to write Measuring the Circle as it stands, even though I cannot describe them precisely since he did not expose them himself, even indirectly. As historians of mathematics, we cannot content ourselves with a superficial reading of the book and offer a historical treatment that would ignore this new dimension that studying Measuring the Circle allows us to perceive. We are committed to try to account for the knowledge the actors we observe possessed and the practices they put into play, even when these were not the objects of discursive exposition.
This example illustrates why, in order to fully accomplish their task, historians must look for clues and then strive to interpret those clues as best as they can. One might of course be tempted to consider this case as an exception and an outlier; however, since I began working as a historian, my experience has convinced me of the contrary, not only because other similar phenomena occur in Li Ye’s book, but because they actually occur much more broadly. In fact, as early as 1974, drawing on discussions with Igor Shafarevich, Isabella Bashmakova once showed something quite similar about the four books of Diophantus’ Arithmetics that still exist in Greek [1 I. G. Bašmakova, Diophant und diophantische Gleichungen. Translated from the Russian 1972 original by L. Boll, Birkhäuser, Basel-Stuttgart (1974) ]. Ten years later, Roshdi Rashed fully developed this approach and observed the same phenomena in his publication of the four other books that had just resurfaced in Arabic [17 R. Rashed, Diophante. Les Arithmétiques, Tome 3: Livre IV. Tome 4: Livre V–VII. Les Belles Lettres, Paris (1984) ]. These historians used insights from modern algebraic geometry to analyze the procedures Diophantus followed in the Arithmetics to solve Diophantine problems. This reading, instrumented by a type of mathematical knowledge that Diophantus certainly did not possess, revealed something that completely contradicted previous interpretations, according to which Diophantus was fundamentally unpredictable in his approach to a problem, even after one has read dozens of his solutions to other problems. Indeed, the analysis of the Arithmetics using algebraic geometry showed that Diophantus’ solutions systematically made use of the same methods. Exactly as was the case for Li Ye, we cannot attribute to Diophantus knowledge of the tool modern historians put into play to read the Arithmetics. However, this tool brings to light knowledge that Diophantus possessed and practices he used without recording them. How can we approach his knowledge and practices on the basis of these clues? This is the theoretical problem raised by these phenomena [3 K. Chemla, What is the content of this book? A plea for developing history of science and history of text conjointly. Philosophy and the History of Science: A Taiwanese Journal4, 1–46 (1995) [Republished in [5]] ].
In the cases of Li Ye and Diophantus, the clues provided by a certain type of mathematical reading reveal facets of the knowledge and practice that these authors have put into play in their approaches to specific problems, without, however, writing about them. In fact, clues can do more for historians, as Anne Robadey has illustrated in her work on Henri Poincaré. For instance, Robadey [18 A. Robadey, A work on the degree of generality revealed in the organization of enumerations: Poincaré’s classification of singular points of differential equations. In Texts, textual acts and the history of science, edited by K. Chemla and J. Virbel, Springer, Dordrecht, 385–419 (2015) ] starts from the remark that Poincaré’s publications abound in enumerations, and she sets out to analyze what these textual phenomena can teach us about the way Poincaré carried out his mathematical work. Robadey [18 A. Robadey, A work on the degree of generality revealed in the organization of enumerations: Poincaré’s classification of singular points of differential equations. In Texts, textual acts and the history of science, edited by K. Chemla and J. Virbel, Springer, Dordrecht, 385–419 (2015) ] establishes that these textual clues reveal an intellectual practice that Poincaré recurrently put into play in different contexts and that left traces not only in his writings but also in the type of mathematical results he formulated. Indeed, faced with certain mathematical situations, Poincaré regularly analyzes them, focusing first on the case that presents itself most often (in a sense of the latter expression for which Poincaré puts forward a definition and an assessment), then on the second most frequent case, and so on, until reaching phenomena that he thinks he can disregard, since they “almost never” occur (on the basis of an assessment of the same type). The enumerations embody precisely this recurring intellectual procedure that Poincaré follows. Moreover, they mesh with theorems of Poincaré’s in which he asserts that something holds true except for a set of situations that can be neglected. In this example, textual phenomena, mathematical practice and mathematical results appear to be closely intertwined. How, as historians, we can find clues that allow us go deeper in our analysis, and how we can use them in historical research are precisely two of the main issues that I study, not least in the context of the project “History of science, history of text”, which I launched in 1995 and on which I have been working since then with a group of colleagues (see, e.g., [5 K. Chemla (ed.), History of science, history of text. Boston Studies in the Philosophy of Science 238, Springer, Dordrecht (2004) ]).
The result obtained by Robadey that I have summarized naturally leads us to another interesting issue: why do practitioners of mathematics not always present their knowledge and practices “explicitly” (as we would be tempted to say, but I explain below why this term is inadequate), to the extent that historians need to rely on clues to uncover part of this knowledge and these practices? The example of Poincaré’s enumerations suggests a first answer to this question. If his publications yield the clues I have mentioned, the reason seems to be that Poincaré carries his analysis forward while engaging with his page. The page thereby keeps the trace of the procedure that recurringly structures his mathematical exploration. This remark explains why the writing gives us clues about his way of conducting mathematical work. Poincaré chooses to work with the textual structure of the enumeration, since it offers a support on which he can rely to unfold his reasoning.
We can observe a similar phenomenon in the prehistory and history of duality, on which I have begun to work with Serge Pahaut [13 K. Chemla and S. Pahaut, Préhistoires de la dualité: explorations algébriques en trigonométrie sphérique (1753–1825). In Sciences à l’époque de la Révolution Française, edited by R. Rashed, Lib. Sci. Tech. Albert Blanchard, Paris, 151–201 (1988) ]. If we considered that duality emerged in mathematics at the point when actors first explicitly mentioned the phenomenon, we would set its beginnings in the 1820s. However, Pahaut and I noticed that starting from the 1750s, some mathematicians who published on spherical trigonometry chose new notations, and shaped types of text, both of which were appropriate to highlight a phenomenon that they had observed without thematizing it. Using new notation, Leonhard Euler, for instance, presented in 1753 a memoir about spherical trigonometry that is remarkable for the following reason: its text displayed, without any comment, a symmetry in a corpus of propositions asserted, and also in a corpus of proofs establishing these propositions. Today, we associate this symmetry with the duality that affects spherical trigonometry. Euler did not address this phenomenon discursively. For him, as for several mathematicians who wrote about spherical trigonometry in the same way in the following decades, this was a phenomenon to be explored, and, instead of writing about it in a discursive way, they expressed what they observed using textual features of their writings: they gave it to readers to read off from the structure of the text. Should we call such a way of expressing knowledge “not explicit” simply because it is not expressed with a subject, a verb and a complement? I don’t think so. This would be quite a narrow interpretation of what “explicit” might mean.
Indeed, we can establish that for these mathematicians, writing in this way was a genuine choice. The reasoning goes as follows. In a second memoir on the topic that Euler presented in 1781, Pahaut and I were able to show that he made a mistake in a proof, which was then replicated in the dual proof. This clue thus indicates that Euler relied on the notation to produce the dual theorem and the dual proof by mere rewriting of the corresponding theorem and proof, without actually redoing the computation. In other words, Euler knew that a theorem and a proof could automatically give rise to another theorem and another proof, but he chose to present both systematically and to cast light on the symmetry between them by means of the structure of his exposition. This remark allows us to establish another key point: the notation appropriate to investigate phenomena related to duality constituted a tool created by Euler to work with and to produce a text that displayed the symmetry. More generally, texts are not always merely discursive expositions of knowledge, as a modern reading all too often expects. This remark might seem obvious for rough drafts, but Euler’s inquiry into duality and Poincaré’s enumerations show that it also applies to texts intended for publication. We see mathematicians shaping notations and textual resources and developing practices using them, in order to work with them and explore new phenomena. As a result, these textual resources and practices present intimate correlations with the questions these actors pursue and the research they conduct. I take these textual innovations as a key dimension of their activity.
This observation highlights one of the reasons why, as a result, texts can give clues about the mathematical work that produced them and also about the knowledge that mathematicians acquired through working with them. In Euler’s case, he met more than once with phenomena caused by duality, and regularly made use of similar textual resources. Interestingly, when dealing with the same topics, subsequent mathematicians used notation and textual resources that were either identical or similar to Euler’s, which indicates that notation and textual resources are, like mathematical theories and concepts, products of mathematical work that get picked up and used further by others [4 K. Chemla, Euler’s Work in spherical trigonometry: Contributions and applications. In Euler. Opera Omnia. Commentationes physicae ad theoriam caloris, electricitatis et magnetismi pertinentes. Appendicem addidit Karine Chemla, edited by P. Radelet-de Grave and D. Speiser, CXXV–CLXXXVII, Birkhäuser, Basel (2004) ]. The joint production of knowledge and textual resources (in the broadest sense of this expression) is likewise one of the theoretical issues that interest me most.
If we pursue this line of thought, we see that sometimes, in order to deal with specific topics, new types of textual resources are introduced (like writing propositions and proofs in a symmetrical way), and that some among the subsequent readers will not only grasp what is being given to read in this new manner, but also then go on to reuse the new textual resources to carry on further research along the same lines. However, not all readers will notice what is given to read in this way. For instance, historians of mathematics had not underline what the structures of these texts expressed, at least for works written before Joseph Diez Gergonne’s explicit introduction, in 1826, of a double-column device to display the symmetry between propositions and proofs elicited by duality [14 J. D. Gergonne, Considérations philosophiques sur les élémens de la science de l’étendue. Ann. Math. Pures Appl. [Ann. Gergonne]16, 209–231 (1825/26) ]. My purpose is not to blame these historians, but to draw a conclusion from this observation. Obviously, we do not all read in the same way, particularly because we have not all been acculturated to reading mathematical writings in the same way. Reading (and reading mathematical texts is no exception) has a history that itself deserves to be studied in the various contexts in which it has been carried out over time, in order to better account for what our sources convey in ways that are not always obvious to us. This latter issue, and more generally those brought to light in this section, have turned out to be central in basically every single piece of research that I have conducted.
2 The Nine Chapters: Algorithms, proofs, and epistemological values
While working on Measuring the Circle, it appeared to me that this book was deeply rooted in an ancient Chinese canonical work in mathematics to which Li Ye explicitly refers, namely the first-century classic The Nine Chapters on Mathematical Procedures (Jiuzhang suanshu 九章算術, hereafter The Nine Chapters). In fact, most mathematical writings composed in China before the fourteenth century referred to this work and to the commentaries with which it has been handed down, that is, Liu Hui’s 劉徽 commentary, completed in 263, and the subcommentary published in 656 by a team working under the supervision of Li Chunfeng 李淳風. When, as early as 1981, Guo Shuchun suggested that we could cooperate to translate The Nine Chapters and its commentaries into French, I thus found the project meaningful and accepted without hesitation. We agreed in 1983 that in addition to the translation, our joint book would offer a new critical edition of these texts as well as our own annotations, unaware that these tasks would take us over twenty years to complete [12 K. Chemla and S. Guo, Les neuf chapitres. Dunod, Paris (2004) ].
The project was difficult not only because the Chinese text was hard and the establishment of the critical edition challenging, but also because the endeavor raised many theoretical problems that I felt we needed to address to complete our task satisfactorily. I will illustrate some of these problems while outlining some of the research directions I have followed in my research on The Nine Chapters and the more theoretical projects that this work has inspired me with.
The Nine Chapters was composed of 246 mathematical problems along with procedures to solve such problems. The “problem and procedure” form had led some historians to read it either as an exercise book or as a manual for bureaucrats, who would simply need to pick up instructions and follow them blindly. It seemed to me that these interpretations, which derived from a modern reading of an ancient text, could not explain why the book had been considered a classic for centuries. We thus needed to find ways of reading The Nine Chapters that could be less anachronistic and for which we could put forward arguments.
My efforts first bore on the procedures. In 1972, Donald Knuth, whose work on algorithms needs no introduction, published an article that had a significant impact on the history of ancient mathematics [16 D. E. Knuth, Ancient Babylonian algorithms. Comm. ACM15, 671–677 (1972) ]. Indeed, his article was proposing a completely new way of approaching cuneiform texts of the beginning of the second millennium BCE, by reading them as they were written, i.e., as lists of operations, or “algorithms”, and not by rewriting them into modern algebraic formulas, as had been the case until then. I became aware of this breakthrough in 1981, thanks to discussions with Wu Wenjun, a topologist who had turned to automated theorem proving and the history of mathematics in China during the cultural revolution [15 J. Hudeček, Reviving ancient Chinese mathematics. Needham Research Institute Studies, Routledge/Taylor & Francis Group, London (2014) ]. Wu immediately adopted Knuth’s perspective in his reading of the procedures contained in ancient Chinese mathematical texts, since they too were written in the form of lists of operations. What mattered most to him was the emphasis that Chinese texts of the past had placed on algorithms providing constructive means to solve problems. A typical example is the algorithm described by Qin Jiushao 秦九韶 in his 1247 book, in order to compute actual solutions to problems whose solution is known to exist by the Chinese remainder theorem [19 W.-T. Wu, Recent studies of the history of Chinese mathematics. In Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Berkeley, Calif., 1986), Amer. Math. Soc., Providence, RI, 1657–1667 (1987) ]. I became more interested in the work with lists of operations to which the procedures of The Nine Chapters attest.
This work is eloquently illustrated by the procedures given in The Nine Chapters for square and cube root extraction, whose texts put into play three operations that Knuth identified as fundamental in the writing of algorithms: assignment of variables, iterations and conditionals. Before Knuth introduced the idea of reading lists of operations as algorithms, historians knew which computations these texts referred to, but I claim they were unable to understand how these texts in The Nine Chapters actually referred to these computations. Thanks to the recent development of mathematical work on algorithms, in relation to their implementation on computers, mathematicians have shaped new types of texts to write procedures, and these textual resources have given us new insights into how ancient procedural texts might have been written and consequently how we might interpret them [10 K. Chemla, From reading rules to reading algorithms. Textual anachronisms in the history of mathematics and their effects on interpretation. In Anachronisms in the history of mathematics, edited by N. Guicciardini, Cambridge University Press, Cambridge (to appear) ]. We see again how, in different contexts, actors put into play different types of textual resources to carry out mathematical work and to write about it. In the case of the procedures of The Nine Chapters, we could not fully interpret their texts and understand the work involved in producing them without first asking ourselves how these texts were expected to be read and how mathematical work put them into play. With respect to, e.g., the algorithms for root extractions, this research brought to light two key points.
First, the way in which the author(s) had used conditionals and iterations to write a list of operations on the basis of which any square (resp. cube) root extraction could be performed highlighted important features of the work with operations in this context. To explain this point, let me make clear that the execution relied on a decimal place-value system and that the roots were determined digit by digit. On this basis, the list of operations used for the first digit and the one used for each digit after the first one had been shaped in such a way that they could be integrated into a single text. Without entering into details (for which I refer to the 2004 book [12 K. Chemla and S. Guo, Les neuf chapitres. Dunod, Paris (2004) ]), let me simply emphasize that the integration relied on the assignment of variables. It also relied on the fact of treating operations formally and without taking their intention into account. More specifically, highlighting an operation common to the concluding part of a root extraction (when the digit of the units has been dealt with) and to the preparation of the computation for the next digit, if any, even though the purpose of using this operation differed in the two contexts, as well as placing the statement of this operation in the list of operations adequately with respect to the conditionals and the iteration, played a key part in allowing the authors to compose a single algorithm valid for all cases. In The Nine Chapters and their commentaries, we find more generally many indications that the authors worked on lists of operations formally, without taking into account the variety of reasons for bringing these operations into play in each of their respective contexts. As a result, we regularly see authors striving to unify lists of operations that performed different tasks, but could be made formally identical. This highlights a form of algebra specific to the work with operations, to which I have devoted some research, but on which much remains to be done.
The latter remarks lead me to the second key point. A search of the kind just described with respect to algorithms, that is, a search for lists of operations whose efficacy would extend as broadly as possible, bespeaks actors’ valuing of generality. The fact of giving a single algorithm for square (resp. cube) root extraction points in the same direction. The text of the algorithm was general in the sense that for any number, an adequate circulation within it, guided by the conditionals and the iteration, would yield the list of operations required to determine the desired square root. What is more, the text added this: should the extraction not be completed when reaching the digit of the units, the result should be given as the “side of the number”, i.e., as a quadratic irrational. If we considered this suggestion from the viewpoint of the discussions about irrationality by Greek authors of antiquity, we would completely miss the point – I return to this below. At stake in the interpretation of the text of the square root algorithm is thus a better appreciation of how it reflects the importance actors in this context gave to the epistemological value of generality.
In fact, generality proved to be a key value for these actors much more broadly [9 K. Chemla, The Motley Practices of generality in various epistemological cultures, The Hans Rausing lecture 2017. Salvia Småskrifter, Uppsala, www.idehist.uu.se/digitalAssets/775/c_775182-l_1-k_2019motley-practices-of-generality–final-versionrausinglecture2017originalcorrected.pdf (2019) ]. For instance, the way in which commentators read problems in The Nine Chapters indicated that for them, a particular problem was to be interpreted as a paradigm. This might seem obvious: the problems from our childhood about trains passing each other were not meant to stand only for themselves, but expressed something more general. However, an observation of the commentators’ way of reading problems in the classic shows that they meant something more specific. In a key case, when the procedure placed after a problem correctly solves it, but lacks generality, the third century commentator Liu Hui expresses dissatisfaction. After pointing out that the procedure of The Nine Chapters is based on the use of two singular characteristics of the problem, he proposes a first procedure that fixes the failure of the original procedure to solve the most general problem, distinguishing between two cases, and then a completely general and uniform procedure. In other words, for Liu Hui, the fact that a mathematical problem was not abstract did not affect the expectation he had with respect to its generality. This remark, inspired by this Chinese document, raised an important theoretical issue: it was an invitation to dissociate the values of generality and abstraction in our reflection about mathematics and to see what a focus on generality alone might show. The emergence of projective geometry in France during the first decades of the 19th century proved to be an ideal case for me to address this issue. Indeed, this new geometry took shape in the hands of Carnot, Poncelet, Chasles and others, on the basis of a comparative reflection about the different types of generality brought about by analytic and geometric approaches to geometric problems. More broadly, this direction of research proved fruitful for a group of historians and philosophers of science, as is illustrated by the collective reflection we developed on this issue [11 K. Chemla, R. Chorlay and D. Rabouin (eds.), The Oxford handbook of generality in mathematics and the sciences, Oxford Univ. Press, Oxford (2016) ].
The remarks that I have presented about the problems of The Nine Chapters illustrate a method that I have used more systematically. Indeed, if we need to restore how ancient actors used and read the texts with which they performed mathematical activity, or, in other words, if we need to develop a history of the reading and handling of ancient mathematical texts, observing how ancient readers proceeded seems to be a method that has great potential. This is precisely one of the reasons why it is so valuable to have early commentaries on The Nine Chapters. If, for instance, we continue to rely on them to better understand how and why ancient actors used problems in their mathematical practice, we discover something quite unexpected, which definitively rules out the interpretation of The Nine Chapters as an exercise book or as a manual for bureaucrats.
This facet of their practice also appears when we turn to another key point about the commentaries on The Nine Chapters, namely that they systematically put forward proofs of the correctness of the algorithms presented in the classic. This is quite an important fact for a history of mathematical proof, to which I return shortly. What matters here is that the commentators’ way of carrying out proving brings mathematical problems into play. To put it differently, in their practice, mathematical problems appear to be tools with which to conduct proofs, and not merely statements awaiting a solution [6 K. Chemla, On mathematical problems as historically determined artifacts: reflections inspired by sources from ancient China. Historia Math.36, 213–246 (2009) ]. If we think that the same fact held true for the author(s) of The Nine Chapters, this invites a radically new interpretation of the work. The reading of problems and procedures that I have suggested might help us understand better how The Nine Chapters has been considered a canonical work over so many centuries. What is more, the fact that The Nine Chapters was handed down with these commentaries might have also played a part in giving the book its value in the eyes of its users. This remark brings us back to the proofs that Liu Hui as well as the team working with Li Chunfeng formulated.
In contrast with what we read in Euclid’s Elements and Archimedes’s writings, these proofs aim at establishing the correctness of procedures. Observing them hence gives us source material to think about this other branch of the history of proof that has so far been almost completely neglected, and, more broadly, about the various dimensions of the exercise of proving in mathematics [8 K. Chemla (ed.), The history of mathematical proof in ancient traditions. Cambridge University Press, Cambridge (2012) ]. What is essential here is that the commentators use theoretical concepts to refer to key aspects of the conduct of a proof.
To begin with, they devote a specific term, i.e., “meaning/intention” (yi 意), to designate the meaning of an operation that corresponds to the interpretation of its result in the context in which the operation is used. Typically, for an operation, this is the kind of meaning that the context of a problem enables a practitioner to make explicit. By extension, the term yi also refers to a sequence of meanings of this kind, and in the end to the reasoning from which the sequence derives. As a rule, a reasoning of this type consists in making clear the “meaning” of the successive steps of an algorithm, thereby showing why its end result corresponds to what was expected. Interestingly, we find here an echo with the type of reasoning Li Ye expounded in his “details of the procedure”, which we mentioned at the beginning of this article. The only difference lies in this: in Li Ye’s case, instead of yielding a meaning and a number, each operation yields a meaning and a polynomial. We nevertheless see that there might be traditions of reasoning to which Chinese writings attest, but which were not yet studied.
The second term used by commentators of The Nine Chapters in the context of their proofs, which I denote by yi’ 義, refers to another type of “meaning” for procedures. It designates a fundamental procedure that underlies the procedure whose correctness must be established. As part of the proof of the correctness, this fundamental procedure highlights the strategy followed by the algorithm under consideration. At the same time, identifying it connects this algorithm with others, which follow the same formal strategy, even though the reasons for using the same operations might differ, depending on the context. The interest that commentators have for this kind of “meaning” thus appears to be connected with the formal work on operations to which the algorithms contained in The Nine Chapters also attest. This focus of their proofs is in fact more broadly connected with a research program for which we have evidence between the first and the thirteenth century and which aimed at identifying the least number of algorithms from which all the others derive [9 K. Chemla, The Motley Practices of generality in various epistemological cultures, The Hans Rausing lecture 2017. Salvia Småskrifter, Uppsala, www.idehist.uu.se/digitalAssets/775/c_775182-l_1-k_2019motley-practices-of-generality–final-versionrausinglecture2017originalcorrected.pdf (2019) ].
The last set of terms that commentators use for their proofs relates to what I have called “algebraic proofs in an algorithmic context”. A proof of this kind consists in establishing a list of operations that starts from the same data as the algorithm under consideration, and yields the desired result. The commentator then takes the algorithm established as correct as a basis, and operates on its list of operations to transform it, qua list of operations, into the algorithm whose correctness is to be established. In other words, instead of rewriting equalities, as we do in an algebraic proof, this type of proof rewrites algorithms. The meta-operations applied to the list of operations include swapping multiplication and division that follow each other, and cancelling a multiplication and a division inverse of one another. They also include inverting an algorithm known to be correct. The essential point here is that the commentators associate the correctness of these meta-operations with the fact that divisions and square root extractions are given exact results, notably through the introduction of fractions and quadratic irrationals. They thus bring the set of numbers used and the meta-operations applied to a list of operations in relation with each other. Moreover, here again, we see that these “algebraic proofs in an algorithmic context” also involve formal work on lists of operations.
What does all this tell us about the history of algebraic proof, of which we still lack a proper account? What does it tell us about the history of algebra and the part played by operations in the history of mathematics? These are some of the theoretical questions that remain on my agenda.
Acknowledgements
I have pleasure in expressing my gratitude to Fernando Manuel Pestana da Costa for his invitation to write this article and Leila Schneps for her feedback, which greatly improved it.
References
- I. G. Bašmakova, Diophant und diophantische Gleichungen. Translated from the Russian 1972 original by L. Boll, Birkhäuser, Basel-Stuttgart (1974)
- K. Chemla, Equations with general coefficients in the Ce Yuan Hai Jing. Publications de l’Institut de Recherche Mathématique de Rennes, Fascicule II: Science, Histoire, Société, 23–30, www.numdam.org/article/PSMIR_1985___2_23_0.pdf (1985)
- K. Chemla, What is the content of this book? A plea for developing history of science and history of text conjointly. Philosophy and the History of Science: A Taiwanese Journal4, 1–46 (1995) [Republished in [5]]
- K. Chemla, Euler’s Work in spherical trigonometry: Contributions and applications. In Euler. Opera Omnia. Commentationes physicae ad theoriam caloris, electricitatis et magnetismi pertinentes. Appendicem addidit Karine Chemla, edited by P. Radelet-de Grave and D. Speiser, CXXV–CLXXXVII, Birkhäuser, Basel (2004)
- K. Chemla (ed.), History of science, history of text. Boston Studies in the Philosophy of Science 238, Springer, Dordrecht (2004)
- K. Chemla, On mathematical problems as historically determined artifacts: reflections inspired by sources from ancient China. Historia Math.36, 213–246 (2009)
- K. Chemla, Une figure peut en cacher une autre. Reconstituer une pratique des figures géométriques dans la Chine du XIIIe siècle. Images des mathématiques, images.math.cnrs.fr/Une-figure-peut-en-cacher-une.html (2011)
- K. Chemla (ed.), The history of mathematical proof in ancient traditions. Cambridge University Press, Cambridge (2012)
- K. Chemla, The Motley Practices of generality in various epistemological cultures, The Hans Rausing lecture 2017. Salvia Småskrifter, Uppsala, www.idehist.uu.se/digitalAssets/775/c_775182-l_1-k_2019motley-practices-of-generality–final-versionrausinglecture2017originalcorrected.pdf (2019)
- K. Chemla, From reading rules to reading algorithms. Textual anachronisms in the history of mathematics and their effects on interpretation. In Anachronisms in the history of mathematics, edited by N. Guicciardini, Cambridge University Press, Cambridge (to appear)
- K. Chemla, R. Chorlay and D. Rabouin (eds.), The Oxford handbook of generality in mathematics and the sciences, Oxford Univ. Press, Oxford (2016)
- K. Chemla and S. Guo, Les neuf chapitres. Dunod, Paris (2004)
- K. Chemla and S. Pahaut, Préhistoires de la dualité: explorations algébriques en trigonométrie sphérique (1753–1825). In Sciences à l’époque de la Révolution Française, edited by R. Rashed, Lib. Sci. Tech. Albert Blanchard, Paris, 151–201 (1988)
- J. D. Gergonne, Considérations philosophiques sur les élémens de la science de l’étendue. Ann. Math. Pures Appl. [Ann. Gergonne]16, 209–231 (1825/26)
- J. Hudeček, Reviving ancient Chinese mathematics. Needham Research Institute Studies, Routledge/Taylor & Francis Group, London (2014)
- D. E. Knuth, Ancient Babylonian algorithms. Comm. ACM15, 671–677 (1972)
- R. Rashed, Diophante. Les Arithmétiques, Tome 3: Livre IV. Tome 4: Livre V–VII. Les Belles Lettres, Paris (1984)
- A. Robadey, A work on the degree of generality revealed in the organization of enumerations: Poincaré’s classification of singular points of differential equations. In Texts, textual acts and the history of science, edited by K. Chemla and J. Virbel, Springer, Dordrecht, 385–419 (2015)
- W.-T. Wu, Recent studies of the history of Chinese mathematics. In Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Berkeley, Calif., 1986), Amer. Math. Soc., Providence, RI, 1657–1667 (1987)
Cite this article
Karine Chemla, All roads come from China – For a theoretical approach to the history of mathematics. Eur. Math. Soc. Mag. 119 (2021), pp. 23–30
DOI 10.4171/MAG/5