An introduction to the mathematics in the Alhambra of Granada

Miguel Ortega

doi:10.4171/mag/246

Every visitor to the Alhambra of Granada is captivated by the beauty of the geometric decoration in the Nasrid Palaces, which are spread across floors, ceilings, windows, doors and walls. In this text, we aim to provide a brief introduction to the mathematical secrets that the artisans and artists likely employed, under modern point of views. We will review some Nasrid decorative elements, rosettes and realizations of plane crystallographic groups.

1 Introduction

Muhammad I ibn al-Ahmar (1195–1273), also known as Alhamar, founded the Nasrid dynasty in 1238, establishing the Emirate of Granada in the south of present-day Spain. It became the only surviving Islamic kingdom in the Iberian Peninsula, while others like Jaén, Córdoba and Seville were defeated by the army led by Ferdinand III of Castile. In fact, Alhamar became a vassal of Ferdinand III, ensuring the survival of the Emirate of Granada for another 250 years. Naturally, everything related to these years in Granada is called Nasrid. King Alhamar first ordered the construction of a fortress on top of a hill. Along the next two centuries, the Nasrid dynasty expanded this original castle into a complex of towers, walls, gardens and palaces, known as the Alhambra. Nasrid artisans and artists brilliantly decorated plenty of places, achieving breathtaking results. In fact, some offices of the Museum of the Alhambra contain several thousand pieces, ranging from single tiles to complete decorative tilings.

Nasrid artisans and artists used basic tools, compared to our modern technology, and a lot of inventiveness to make extremely beautiful decorative creations out of plaster and tiles. From a mathematical point of view, they used a deep knowledge of Euclidean geometry, and intuitive ideas of the four rigid movements of the plane, namely, translations, rotations, reflections and glides (or glide reflections).

We will pay attention to Nasrid decorative elements, rosettes and examples of crystallographic groups. Also, we will provide some hints of how to construct them. However, the reader should be aware that we cannot go into much detail. Instead, one can consult various books that summarize endless hours of work by many authors. We just cite a few. The contributions of Rafael Pérez-Gómez are important, see for example [⁠7⁠ R. Pérez-Gómez, The four regular mosaics missing in the Alhambra. Comput. Math. Appl. 14, 133–137 (1987) ] and [⁠1⁠ M. Angustias Cabrera et al., 7 paseos por la Alhambra. Proyecto Sur de Ediciones, Granada, Spain (2007) ]. Also, the three secondary school teachers Francisco Fernández, Joaquín Valderrama and Antonio Fernández wrote the book [⁠3⁠ F. Fernández Morales, J. Valderrama Ramos and A. Fernández Juárez, The mathematical Alhambra: The beauty of Nasrid architectural capriccio. Gami, Granada, Spain (2024) ] to summarize a life-long task of showing the many mathematical secrets of the Alhambra to their students, in just 471 pages. In addition, Manuel Martínez Vela’s book [⁠5⁠ M. Martínez Vela, The Alhambra with a ruler and compass: A step-by-step outlining of tiling and plasterwork. 3rd ed. Almizate, Alcalá la Real, Spain (2022) ] can be seen as an introductory textbook of the drawings in the Alhambra, with 226 pages, in which the author explains step by step how to draw the most famous tilings found there. By the same author, the book [⁠4⁠ M. Martínez Vela, Cómo dibujar los mosaicos de la Alhambra. Almizate, Alcalá la Real, Spain (2022) ] is a second and much bigger project with the same aim, but 608 pages. Most of the drawings in the present paper are based on Manuel Martínez Vela’s books.

2 Nasrid decorative elements

*Figure 1.* Walls in the Court of the Myrtles, full of pajaritas. 🅭🅯 CC BY 4.0

One can reasonably assert that all geometric, decorative constructions in the Alhambra are based on lattices of squares, equilateral triangles, or a mixture of squares and rectangles. In the following subsections, we select just three of the typical Nasrid decorative elements, among many.

2.1 The Nasrid pajarita (bow-tie)

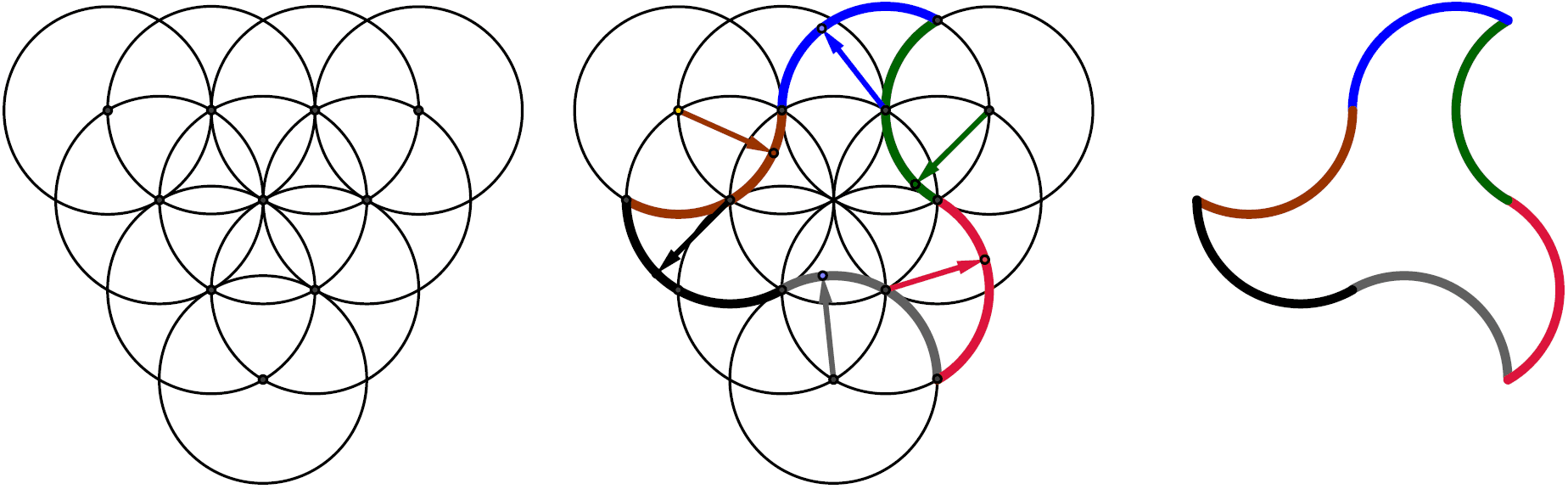
This is the very symbol of the Alhambra. In fact, when entering some villages close to Granada, the typical advertisement ‘Welcome to…’ is illustrated with three or more Nasrid pajaritas. For example, there are a few walls in the Court of the Myrtles full of pajaritas. See Figure ⁠1⁠. In order to draw them, we make a lattice of circles with the same radius. Finally, we choose the suitable arcs. See Figure ⁠2⁠.

*Figure 2.* Steps to draw one pajarita. 🅭🅯 CC BY 4.0

2.2 The bone

This pattern can be found in the Chamber of Ambassadors, which is one of the main rooms of the Nasrid Palaces. One way to draw it is to make a lattice of squares, and then choose the right sides. The heads are just made by drawing the diagonals of the correct squares. See Figures ⁠3⁠ and ⁠4⁠.

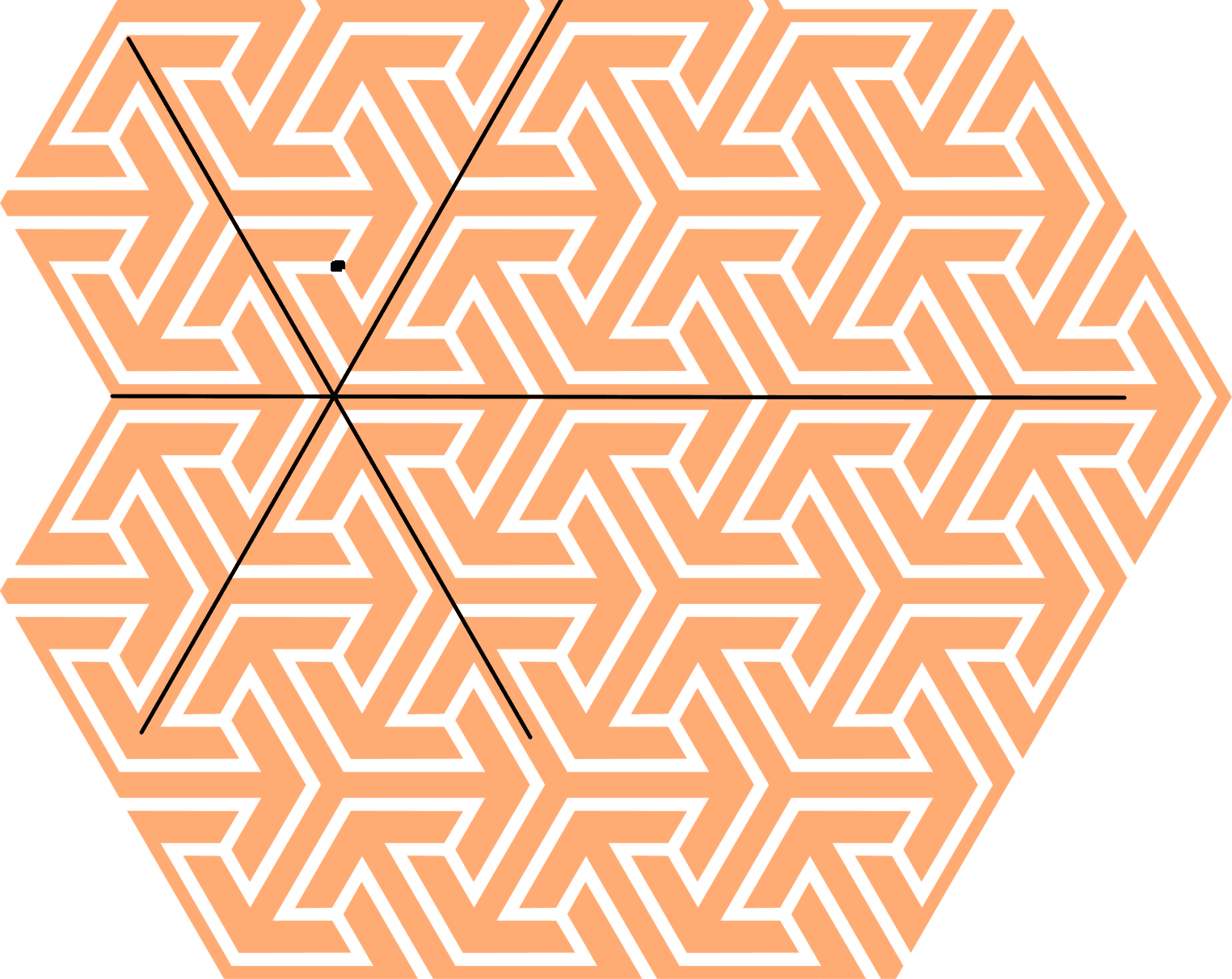
*Figure 3.* Wall in the Chamber of Ambassadors. 🅭🅯 CC BY 4.0

*Figure 4.* Steps to construct the Nasrid *bone*. 🅭🅯 CC BY 4.0

2.3 The airplane

At the entrance to the Chamber of Ambassadors, on both walls, there are two nicely decorated alcoves called tacas. Inside, you can see a tiling of black and white figures called airplanes, see Figure ⁠5⁠.

*Figure 5.* A tiling of black and white *airplanes*, Chamber of Ambassadors. 🅭🅯 CC BY 4.0

We start with a regular octagon. Then, we expand the sides until they meet, and draw some diagonals. Next, we remark the desired sides. We will return to this example later. See Figure ⁠6⁠.

*Figure 6.* A regular octagon with expanded sides and some diagonals, and a black airplane. 🅭🅯 CC BY 4.0

3 Rosettes

The main idea is to draw a figure which rotates around a fixed point (the center) a finite number of times, returning to the original position. A reflection axis containing the center is also possible. In the Alhambra, there are rosettes almost everywhere, which were used to decorate walls, windows, false windows, ceilings, doors, etc.

Definition 3.1. Let $Iso (R^{2})$ be the group of (affine) isometries of the Euclidean plane. A rosette is a plane figure $F$ whose symmetry group

G = {f \in Iso (R^{2}) : f (F) = F}

is finite, with at least two elements. A group of Leonardo is a finite subgroup of $Iso (R^{2})$ with at least two elements.

Note that the identity map is an isometry of any plane figure, regardless of its shape. This is why we assume that there exists at least another isometry.

*Figure 7.* Ceiling of the Room of Abencerrajes. 🅭🅯 CC BY 4.0

Theorem 3.2.

The only possible groups of Leonardo are (isomorphic to) either:

A cyclic group generated by a rotation of center $O$ and angle $2 π / n$ , where $n \in N$ , $n \geq 2$ .
A dihedral group generated by a rotation of center $O$ and angle $2 π / n$ , where $n \in N$ , $n \geq 2$ , and a reflection whose axis contains the center $O .$

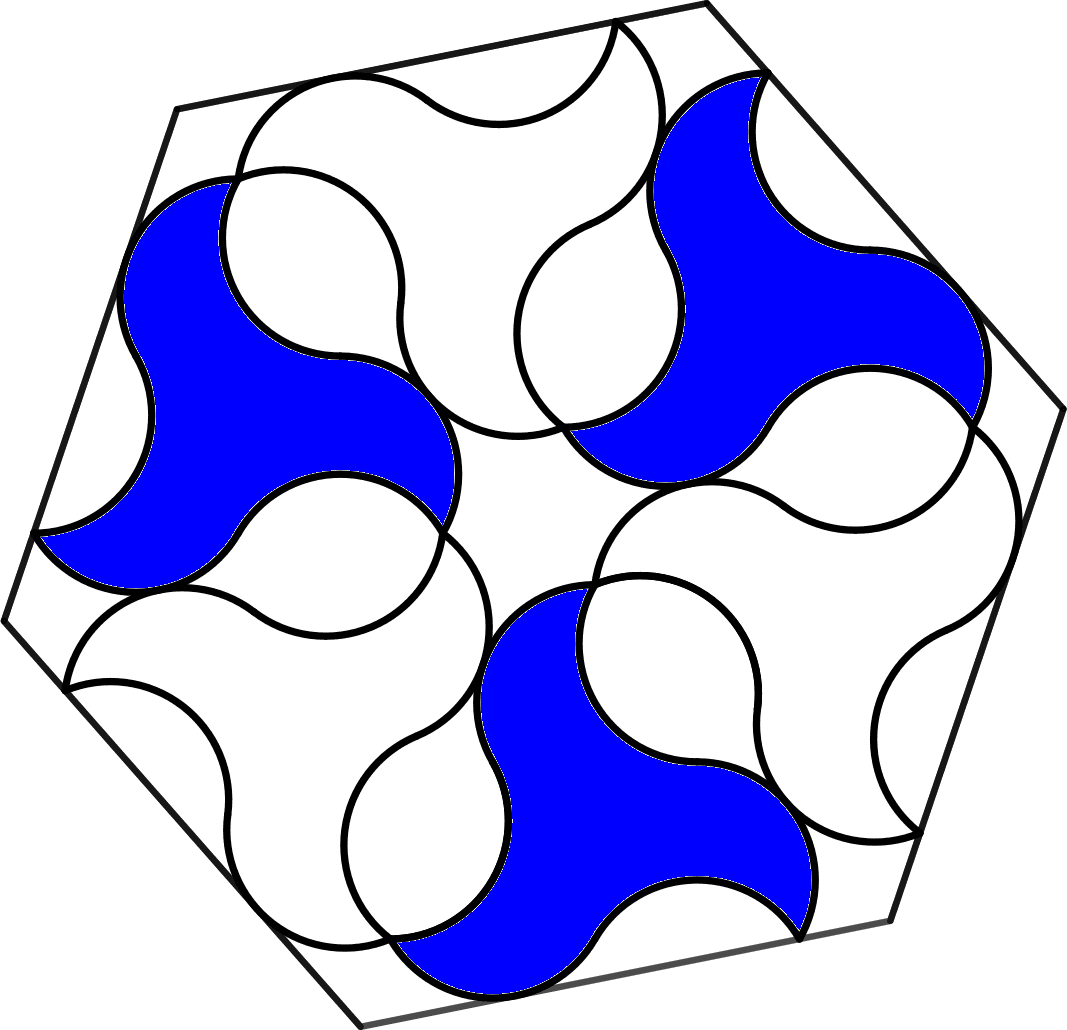
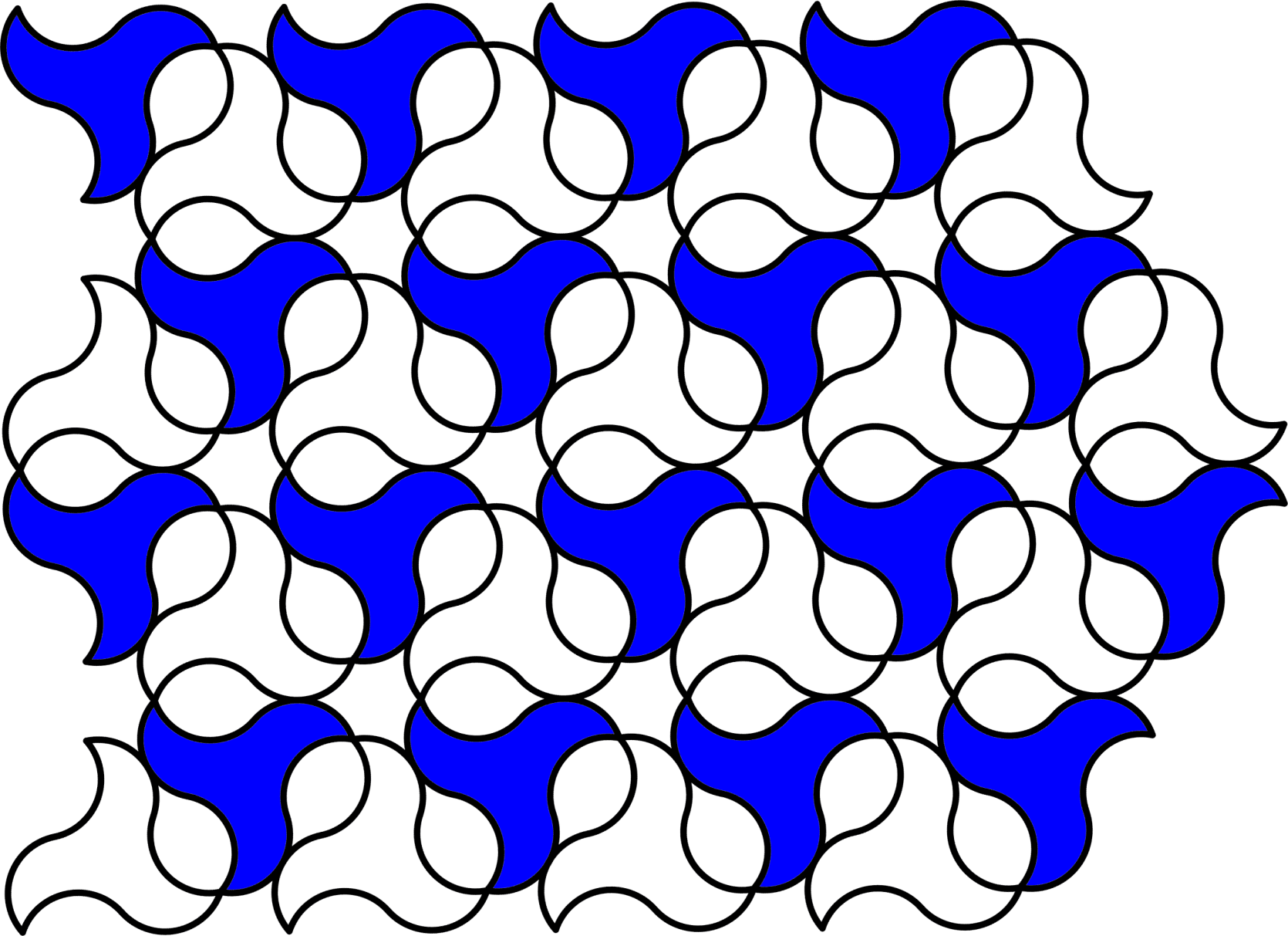
We will call the natural number $n$ the order of the rosette. In this way, there exist only two types of rosettes, namely cyclic or dihedral. The first one can only admit rotations, and the second one both rotations and symmetries. We show a few examples in Figures ⁠7⁠, ⁠8⁠, ⁠9⁠, ⁠10⁠ and ⁠11⁠.

*Figure 8.* Rosette at Mexuar. 🅭🅯 CC BY 4.0

*Figure 9.* Chamber of Ambassadors. 🅭🅯 CC BY 4.0

*Figure 10.* The Partal (on the left) and Court of the Lions (on the right). 🅭🅯 CC BY 4.0

*Figure 11.* Room of the Two Sisters. 🅭🅯 CC BY 4.0

3.1 The incredible case of the regular nonagon

It is well known that the regular nonagon is not constructible with ruler and compass. However, it is possible to find examples of rosettes of order nine in the Nasrid Palaces. We show four examples in Figures ⁠13⁠, ⁠15⁠, ⁠14⁠, ⁠16⁠.

Before the wide adoption of personal computers, architects and draftsmen used two right triangles known as set squares, usually of two types: The first one with two angles of $π /4$ and the second one with angles of $π /3$ and $π /6$ . Arabic artisans also used right triangles to make their designs, according to the book written by Diego López de Arenas between 1613 and 1619, see [⁠6⁠ E. Nuere, La carpintería de lo blanco: Lectura dibujada del primer manuscrito de Diego López de Arenas. Ministerio de Cultura, Madrid, Spain (1985) ] and [⁠1⁠ M. Angustias Cabrera et al., 7 paseos por la Alhambra. Proyecto Sur de Ediciones, Granada, Spain (2007) ]. In fact, there were two families of right triangles, namely, cartabones and ataperfiles. For each cartabon there was the corresponding ataperfil, whose smaller angle was half of the smaller angle of the cartabon. With them, it was possible to divide the straight angle into several equal angles, taking the possible values 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18 and 20, see [⁠1⁠ M. Angustias Cabrera et al., 7 paseos por la Alhambra. Proyecto Sur de Ediciones, Granada, Spain (2007) ].

*Figure 12.* Splitting a straight angle into five equal angles with a cartabon. 🅭🅯 CC BY 4.0

*Figure 13.* Rosette of order 9, wooden ceiling. 🅭🅯 CC BY 4.0

*Figure 14.* Rosette of order 9, false window, Court of the Myrtles. 🅭🅯 CC BY 4.0

*Figure 15.* Rosette of order 9, Room of Abencerrajes. 🅭🅯 CC BY 4.0

*Figure 16.* Rosette of order 9, Point of Observation of Daraxa. 🅭🅯 CC BY 4.0

We know that it is mathematically impossible to obtain some of such angles with ruler and compass, according to the theorem of classification of constructible regular polygons. However, we should recall that in the 20th century, it was possible to construct protractors, which divided a straight angle in 180 equal parts, by accepting a small enough error. Now, in the 21st century, the user of some software can set the accuracy to make drawings.

We note that Manuel Martínez Vela in [⁠4⁠ M. Martínez Vela, Cómo dibujar los mosaicos de la Alhambra. Almizate, Alcalá la Real, Spain (2022) , pp. 366–371] obtained a method to construct a rosette of order nine with an error of just 0.2 degrees, which is a very good achievement.

The amazing fact is that the Nasrid artisans were able to construct all these cartabones and ataperfiles with high precision, bearing in mind the available technology in the Middle Ages.

4 Crystallographic groups

Definition 4.1. A plane crystallographic group is a discrete subgroup of the affine isometries of $R^{2}$ whose subgroup of translations is generated by two linearly independent minimal translations.

Theorem 4.2 (Crystallographic restriction).

Let $r_{θ, c} : R^{2} \to R^{2}$ be a rotation of angle $θ \in] 0, 2 π [$ and center $c \in R^{2}$ . If $r_{θ, c}$ is an element of a plane crystallographic group, then there exists $m \in {2, 3, 4, 6}$ such that $r_{θ, c} \circ \dots m \circ r_{θ, c} = Id$ (identity map).

As an element of a group, the order of $r_{θ, c}$ can only be $m = 2, 3, 4$ or $6$ . The point $c$ is called a center of rotation or order $m$ . Note that the minimal angle of rotation can only be $π$ $(m = 2)$ , $2 π /3$ $(m = 3)$ , $π /2$ $(m = 4)$ or $π /3$ $(m = 6)$ . For our purposes, we introduce now Conway’s notation, [⁠2⁠ J. H. Conway, H. Burgiel and C. Goodman-Strauss, The symmetries of things. A K Peters, Wellesley, MA (2008) ], with a little change. In the book [⁠2⁠ J. H. Conway, H. Burgiel and C. Goodman-Strauss, The symmetries of things. A K Peters, Wellesley, MA (2008) ], the glide reflections are called miracles, but we avoid this term.

$o$ : Only translations. $*$ : Reflections with respect to an axis. $\times$ : Glide reflection (axis and translation vector). $* n$ : When $n$ different axes of reflection intersect at one point, called rotation point. $* n p$ : When $n$ axes of reflection intersect at one point, and also $p$ axes of reflection intersect at another point. $m$ : A center of rotation of order $m$ not included in any reflection axis, called gyration point.

Always, $n, m, p \in {2, 3, 4, 6}$ , according to the Crystallographic Restriction Theorem. With this notation, we completely determine a group by its generators. To simplify notation, we discard the translations. A suitable description is called a signature.

Examples

$* *$ Two parallel axes of reflection. $* \times$ An axis of reflection and a glide reflection whose axis is parallel to the first axis. $2 * 22$ First, the blue $2$ stands for a $gyration point$ of order 2. Next, the red $* 22$ indicates that there are two reflection axes at one point, but also another pair of axes intersecting at a different point. $632$ A gyration point of order 6, another gyration point of order 3, and finally a gyration point of order 2. There are no reflection axes in this case. $2222$ Four different gyration points of order $2$ .

Theorem 4.3 (Classification of plane crystallographic groups).

Up to isometry, there are 17 different plane crystallographic groups, described by their signature: $o$ , $* *$ , $* \times$ , $\times \times$ , $2222$ , $* 2222$ , $2 * 22$ , $22 \times$ , $22 *$ , $333$ , $* 333$ , $3 * 3$ , $442$ , $* 442$ , $4 * 2$ , $632$ , $* 632$ .

Some authors complain that, sometimes, the painting, tiling, or the decorative motive made of plaster is not big enough to be properly considered an example or realization of a plane crystallographic group. However, in all the examples shown in this paper, the main idea is there, up to the size of the tiling or plaster artwork. That is to say, even though the given realization or construction is not a perfect crystallographic group, I would like to think that, indeed, just by chance or by good luck, these geniuses were able to find all possible combinations without knowing it.

In the following list of Figures from ⁠17⁠ until ⁠33⁠, I provide the Conway signature, a basic explanation, and the place. To be honest, the last example (Figure ⁠33⁠) in our list is a bit complicated. It is unknown where this example was exactly located. According to [⁠1⁠ M. Angustias Cabrera et al., 7 paseos por la Alhambra. Proyecto Sur de Ediciones, Granada, Spain (2007) , p. 500], there is an original hexagonal piece of ceramic, with register number 1295.

*Figure 17.* (1) $\times \times$ – Glide reflections with parallel axes. Painting, Wine Gate. 🅭🅯 CC BY 4.0

*Figure 18.* (2) $22 \times$ – A glide and two gyration points of order 2. Ceiling, Wine Gate. 🅭🅯 CC BY 4.0

*Figure 19.* (3) $3 * 3$ – A gyration point of order 3, and three axes intersecting at a point. Paint, Wine Gate. 🅭🅯 CC BY 4.0

*Figure 20.* (4) $* *$ – Parallel reflection axes. Column, Golden Patio. 🅭🅯 CC BY 4.0

*Figure 21.* (5) $22 *$ – Two gyration points of order 2, and a reflection axis. Fountain, Golden Patio. 🅭🅯 CC BY 4.0

*Figure 22.* (6) $o$ – Only translations. Court of the Myrtles. 🅭🅯 CC BY 4.0

*Figure 23.* (7) Recall Figure ⁠5⁠. $2 * 22$ – One gyration point of order 2, and perpendicular axes of reflection. Chamber of the Ambassadors. 🅭🅯 CC BY 4.0

*Figure 24.* (8) $* \times$ – A reflection and a glide reflection with parallel axes. Chamber of Ambassadors. 🅭🅯 CC BY 4.0

*Figure 25.* (9) $* 442$ – Four reflection axes intersecting at one point. Room of the Ship. 🅭🅯 CC BY 4.0

*Figure 26.* (10) $* 632$ – Six reflection axes intersecting at one point. Court of the Myrtles. 🅭🅯 CC BY 4.0

*Figure 27.* (11) $* 333$ – Three points are the intersection of three reflection axes. Court of the Lions. 🅭🅯 CC BY 4.0

*Figure 28.* (12) $* 2222$ – Four points are the intersection of two orthogonal reflection axes. Hall of the Kings. 🅭🅯 CC BY 4.0

*Figure 29.* (13) $632$ – Gyration points of orders 6, 3 and 2. Hall of the Kings. 🅭🅯 CC BY 4.0

*Figure 30.* (1) $442$ – Gyration points of orders 4 and 2. Hall of the Kings. 🅭🅯 CC BY 4.0

*Figure 31.* (15) $4 * 2$ – A gyration point of order 4, and two reflection axes intersecting at a point. The Infant’s Tower. 🅭🅯 CC BY 4.0

*Figure 32.* (16) $2222$ – Gyration points of order 2. Generalife, Tower of Ismail I.

*Figure 33.* (17) $333$ – Gyration points of order 3. The structure of the drawing and the hexagonal shape can only lead to this $333$ example. 🅭🅯 CC BY 4.0

5 A few words of gratitude

When the author was a young assistant professor in Granada University, professors Rafael Pérez Gómez and Ceferino Ruiz Garrido introduced him to the marvelous world of the mathematics in the Alhambra. Bearing in mind the background of the ‘World Mathematical Year 2000,’ professor Pérez Gómez made up a first mathematical visit, and this author participated as one bumbling mathematical guide. Since then, the author has been teaching this subject to his students, as well as promoting it in talks for the general public.

Finally, the author wishes to thank the Patronato de la Alhambra y Generalife, and especially Silvia Pérez López, who works at the Fondo del Museo, for her kindness. Without her help, his student Elora Prados Raya would have never made the video about the crystallographic groups in the Alhambra.⁠¹⁠https://www.youtube.com/watch?v=wl4h0Wot6cY

Remark. All photos were taken by Miguel Ortega or Raquel Máiquez Sáez. All drawings made by Miguel Ortega.

Funding. M. Ortega was partially supported the Spanish MICINN and ERDF project PID2020-116126GB-I00.

Miguel Ortega graduated in mathematics at the University of Granada in 1995. He worked at the University of Huelva (Spain) for one academic year, until September 1998, when he obtained a research grant in Japan and moved to Okayama in October 1998. He defended his PhD in Granada in March 1999, and then stayed at the Shimane University (Japan) until September 1999. In October 1999, he began working as an assistant professor in Granada, where he is currently an associate professor. miortega@ugr.es

¹
https://www.youtube.com/watch?v=wl4h0Wot6cY

References

M. Angustias Cabrera et al., 7 paseos por la Alhambra. Proyecto Sur de Ediciones, Granada, Spain (2007)
J. H. Conway, H. Burgiel and C. Goodman-Strauss, The symmetries of things. A K Peters, Wellesley, MA (2008)
F. Fernández Morales, J. Valderrama Ramos and A. Fernández Juárez, The mathematical Alhambra: The beauty of Nasrid architectural capriccio. Gami, Granada, Spain (2024)
M. Martínez Vela, Cómo dibujar los mosaicos de la Alhambra. Almizate, Alcalá la Real, Spain (2022)
M. Martínez Vela, The Alhambra with a ruler and compass: A step-by-step outlining of tiling and plasterwork. 3rd ed. Almizate, Alcalá la Real, Spain (2022)
E. Nuere, La carpintería de lo blanco: Lectura dibujada del primer manuscrito de Diego López de Arenas. Ministerio de Cultura, Madrid, Spain (1985)
R. Pérez-Gómez, The four regular mosaics missing in the Alhambra. Comput. Math. Appl. 14, 133–137 (1987)

Cite this article

Miguel Ortega, An introduction to the mathematics in the Alhambra of Granada. Eur. Math. Soc. Mag. 135 (2025), pp. 12–19

DOI 10.4171/MAG/246

🅭🅯

This open access article is published by EMS Press under a CC BY 4.0 license, with the exception of logos and branding of the European Mathematical Society and EMS Press, and where otherwise noted.

Back to Issue 135

[bib-bib1] M. Angustias Cabrera et al., 7 paseos por la Alhambra. Proyecto Sur de Ediciones, Granada, Spain (2007)

[bib-bib2] J. H. Conway, H. Burgiel and C. Goodman-Strauss, The symmetries of things. A K Peters, Wellesley, MA (2008)

[bib-bib3] F. Fernández Morales, J. Valderrama Ramos and A. Fernández Juárez, The mathematical Alhambra: The beauty of Nasrid architectural capriccio. Gami, Granada, Spain (2024)

[bib-bib4] M. Martínez Vela, Cómo dibujar los mosaicos de la Alhambra. Almizate, Alcalá la Real, Spain (2022)

[bib-bib5] M. Martínez Vela, The Alhambra with a ruler and compass: A step-by-step outlining of tiling and plasterwork. 3rd ed. Almizate, Alcalá la Real, Spain (2022)

[bib-bib6] E. Nuere, La carpintería de lo blanco: Lectura dibujada del primer manuscrito de Diego López de Arenas. Ministerio de Cultura, Madrid, Spain (1985)

[bib-bib7] R. Pérez-Gómez, The four regular mosaics missing in the Alhambra. Comput. Math. Appl. 14, 133–137 (1987)