At the crossroads of simulation and data analytics

1 Introduction

When identifying, within EU-MATHS-IN, a subject that would rally a majority of companies, from banks to aeronautics, from the health sector to the need of renewal in the energy business, Digital Twins emerged as a rather natural choice [⁠17⁠ EU-MATHS-IN Industrial Core Team, Modelling, simulation and optimization in a data rich environment: a window of opportunity to boost innovation in Europe. Foundation EU-MATHS-IN, European Service Network of Mathematics for Industry (2018) ].

The concept was first created by NASA. Throughout its entire life cycle, a product or process can be accompanied by a virtual representation, called its Digital Twin. Digital Twins allow novel digital assistance for design optimisation, process control, lifecycle management, predictive maintenance, or risk analysis. Digital Twins have become so important to business today that they were identified as one of Gartner’s Top 10 Strategic Technology Trends [⁠18⁠ D. Hartmann and H. Van der Auweraer, Digital twins. Siemens. arXiv:2001.09747 (2019) , ⁠27⁠ M. Kerremans, D. Cearley, A. Velosa and M. Walker, Top 10 strategic technology trends for 2019: digital twins.www.gartner.com/en/documents/3904569/top-10-strategic-technology-trends-for-2019-digital-twin, Gartner (2019) , ⁠47⁠ Digital twins – explainer video. youtu.be/ObGhB9CCHP8, Siemens AG (2019) ]. They are becoming a business imperative, covering the entire lifecycle of an asset or process and forming the foundation for connected products and services. New business opportunities will emerge, benefitting from the cooperation between large companies, SMEs, startups and academia. To turn this vision into reality, novel mathematical and computer science technologies are required to describe, structure, integrate and interpret across many engineering disciplines.

Supporting this development requires a combination of efforts. High fidelity modelling is key to account for multi-physics and multi-scale systems, and to identify new design levers at the smallest scales. It is often derived from first principle approaches and relies on the power provided by High Performance Computing to deliver the expected prediction in a reasonable time frame. On the other hand, reduced order modelling must provide real-time estimates to enable system optimisation, or in combination with statistical learning to achieve efficient modelling compliant with available data in real time during operation. An example of that kind of need is given by autonomous transport. In particular, corresponding solutions must be realised on the edge to provide sufficiently fast and robust interactions with the real process. The fields of application are growing rapidly in the health sector (e.g., www.digitwin.org) and in climate monitoring [⁠3⁠ P. Bauer, B. Stevens and W. Hazeleger, A digital twin of earth for the green transition. Nature Climate Change11, 80–83 (2021) ].

Key to digital twinning is a joint use of data and first principle approaches. In the frequent cases where large amounts of data prove not to be available, this complementarity makes it possible to realise Smart Data concepts, fostering the efficiency and the robustness of predictions and enabling the quantification of associated uncertainties and risks.

The economic impact of related applications is estimated to cover a worldwide market of 90 billion euros per year by 2025. These opportunities are clearly reinforced by the high concentration of simulation firms in Europe, the highest in the world. Europe also benefits from a long-standing proficiency in mathematics. Several reports [⁠11⁠ CMI, Etude de l’impact socio-économique des mathématiques en france [CMI, A study of the soci-economical impact of mathematics in France] (2015) , ⁠14⁠ Deloitte, Measuring the economic benefits of mathematical sciences research in the UK. Deloitte (2012) , ⁠15⁠ Deloitte, Mathematical sciences and their value for the dutch economy. Deloitte (2014) ] have additionally shown the economic impact of mathematical sciences in the US, the Netherlands and France. Furthermore, US studies [⁠41⁠ NSF and WTEC, www.nsf.gov/pubs/reports/sbes_final_report.pdf; www.wtec.org/sbes/SBES-GlobalFinalReport.pdf. ] in the past have also highlighted the European strength in the field.

This being said, the combined use of statistical learning and first principle modelling is not new. Model calibration is an old topic. The Kalman filter lay at the core of space conquest, and has been essential in the efficient control of remote systems. There remain, however, several challenges for achieving a clever way of combining simulation methods for complex systems, data collection, correction procedures and uncertainty quantification. Besides this, Digital Twins are expected to become self-learning objects that can actually provide guidance and high level services in operation, digesting sensor data with the help of reduced models. A significant part of these ambitions relies on a set of mathematical methods as well as integrated environments.

2 A favourable environment

2.1 European Commission Programs

Horizon Europe⁠²⁠ec.europa.eu/info/horizon-europe_en is a Research and Innovation funding program that is in place until 2027, with a total budget of 95.5 billion euros. Its three pillars are (I) Excellent Science, (II) Global Challenges and European Industrial Competitiveness, (III) Innovative Europe. The European Research Council (President: J.-P. Bourguignon) supports pillar I, while the DG Connect Directorate (Dir: K. Rouhana) specifically supports the present topic, as well as High Performance or Quantum Computing, as part of pillar II. Calls are the mechanisms through which individual projects get funded.

Of key importance is the EuroHPC Joint Undertaking. This is a joint initiative between the EU, European countries and private partners to develop a World Class Supercomputing Ecosystem in Europe. The initiative has two major partners onboard: ETP4HPC and the Big Data Value Association, which reflects the ambition to establish synergies between highly accurate simulations and data analytics. It is also oriented towards large companies and SMEs, in order to boost innovation potential and competitiveness, while widening the use of HPC in Europe. EU-MATHS-IN is involved in the TransContinuum Initiative, as a binding effort between ETP4HPC and BDVA, and contributes to a Strategic Research Agenda coordinated by Zoltán Horváth.

2.2 Some open platforms and funded projects

Open software enables new actors including SMEs, potentially with the help of a proper knowledgeable accompaniment, to access highly technological solutions, develop new ideas and start new businesses depending on associated exploitation rights. It clearly shifts development effort from low-value work to value creation. Open platforms can also act as binding environments to interface commercial products with clear added value. Sharing software components between academia and industry may be a way to reinforce the European momentum on the development of new mathematical algorithms in order to, e.g., take advantage of new European HPC architectures or data-simulation hybridation. The development of better interoperability is expected to accelerate innovation and boost European leadership.

Open software has been developed ranging from simulation tools to data analysis with applications like mechanics or biology. Furthermore, it has clearly evolved to provide integrated environments, especially relying on Python interfacing which is a key element to foster collaboration, to integrate various expertises and to make content widely accessible. Let us mention here two projects supported by the European Community that clearly support this ambition.

MSO4SC

Societal challenges are increasing in complexity, and contributing to their resolution requires a holistic approach. It is necessary to provide decision-makers with tools that allow long-term risk analysis, improvements or even optimisation and control. One of the key technologies in this process is the use of mathematical Modelling, Simulation and Optimisation (MSO) methods, which have proven to be effective tools for solving problems such as the realistic prediction of wind fields, solar radiation, air pollution and forest fires, prediction of climate change, improving the filtration process for drinking water treatment and optimisation methods for intensity-modulated radiation therapy. These methods are highly complex and are typically processed via the most modern tools of ICT, including high performance computing and access to big data bases; they usually require the support of skilled experts, who are often not available, in particular in small and medium-sized businesses. The main goal of this project is to construct an e-infrastructure that provides, in a user-driven, integrative way, tailored access to the necessary services, resources and even tools for fast prototyping, also providing the service producers with the mathematical framework. The e-infrastructure consists of an integrated MSO application catalogue containing models, software, validation and benchmark and the MSO cloud, a user-friendly cloud infrastructure for selected MSO applications and developing frameworks from the catalogue. This will reduce the ‘time-to-market’ for consultants working on the above-mentioned societal challenges.

Open Dream Kit

OpenDreamKit is a project that brings together a range of projects and associated software to create and strengthen virtual research environments. The most widely-used research environment is the Jupyter Notebook from which computational research and data processing can be directed. The OpenDreamKit project provides interfaces to well-established research codes and tools so that they can be used seamlessly and combined from within a Jupyter Notebook. OpenDreamKit also supports open source research codes directly by investing into structural improvements and new features to not only connect all of these tools, but also enrich them and make them more sustainable.

3 A mathematical toolbox

We emphasise here four complementary perspectives on the joint exploitation of simulation and data: (i) techniques coming from optimal command, ranging from calibration to filtering, that allow identification of hidden parameters, model correction and handling noisy forcing terms, (ii) solution space reduction that enables fast solving and efficient correction, (iii) multi-fidelity co-kriging in order to merge and prioritise the feedback issuing from simulations and measurements on given observables, (iv) physics-inspired neural networks that directly learn the model solution, based on an a priori (set of) underlying model(s). Each of these approaches corresponds to a different balance in the roles of physical models and collected data. In this text, we do not claim any exhaustivity, and mathematical descriptions will remain formal. The idea is to provide a fairly broad overview of the field while remaining accessible to the vast majority of mathematician readers.

3.1 Optimal control: From calibration to filtering

General setting

Let $\Lambda$ be a vector space of parameters. For every $\lambda \in \Lambda$, the solution $u_{\lambda }\in \mathcal{U}$ of the “best-knowledge” model is defined to be the solution of the partial differential system

in a weak formal form, where $\mathcal{V}$ is a Hilbert space and ${\mathcal{V}}^{\ast }$ its dual. The parameter space $\Lambda$ encompasses modelling choices, the domain shape and the boundary conditions, as well as forcing terms.

Additionally, the physical quantity

is known, potentially with some noise, at the sampling points $({\lambda }_k)\in \Lambda$ as $({\mathbb{Z}}_k)$. The purpose of our quest is to take benefit from this information to estimate $Z(\lambda )$ outside the sampling points, or to improve the solution $u_{\lambda }$ itself given by the model.

Calibration and model correction

As an example, let us augment $\Lambda$ into $\Lambda \times \mathcal{V}$ in order to account for a modelling error term in $\mathcal{V}$ as we consider the augmented system

where $\xi \in \mathcal{V}$. For each sampling point ${\lambda }_k$, the idea is to find the most adequate parameter $\lambda$ of the model close to ${\lambda }_k$ and the model correction $\xi \in \mathcal{V}$ in order to best account for the measurement ${\mathbb{Z}}_k$. The calibration and model correction in the vicinity of ${\lambda }_k$ can be formulated as finding

where $\mathcal{A}(\lambda ,u)+\xi =0$ in ${\mathcal{V}}^{\ast }$, and $|\cdot |$ stands for the Hilbertian norms in $\mathcal{Z}$, $\Lambda$ and $\mathcal{V}$. The scalar coefficients $\alpha ,\beta \in {\mathbb{R}}_{+}^{\ast }$ are taken sufficiently large. As classically given by the techniques of optimal control [⁠30⁠ J.-L. Lions, Contrôle optimal de systèmes gouvernés par des équations aux dérivées partielles. Dunod, Paris; Gauthier-Villars, Paris (1968) ], the solution is characterised by the following system:

in ${\mathcal{V}}^{\ast }$, ${\mathcal{U}}^{\ast }$ and ${\Lambda }^{\ast }$ respectively, with $\Delta =J(\lambda ,u)-{\mathbb{Z}}_k$. Equation (⁠3⁠) is called the adjoint problem and equation (⁠4⁠) defines the gradient of the cost function with respect to $\lambda$, that must vanish. The gradient expression enables an iterative calibration in order to avoid the resolution of the coupled system (⁠2⁠)–(⁠3⁠)–(⁠4⁠). One has ${\xi }_k^{\ast }=-\frac{1}{\beta }p$ and we use the notation $p_k^{\ast }:=p$ in $\mathcal{V}$.

Once the calibration and error corrections are performed at sampling points, let us introduce the functions ${\hat{\lambda }}^{\ast }(\lambda ),{\hat{\xi }}^{\ast }(\lambda ),{\hat{p}}^{\ast }(\lambda )$ obtained by kriging under the form

that comply with values $({\lambda }_k^{\ast })$, $({\xi }_k^{\ast })$, $(p_k^{\ast })$ at sampling points $({\lambda }_k)$. For every $\lambda \in \Lambda$, an updated model can be formulated as finding the solution ${\hat{u}}_{\lambda }\in \mathcal{U}$ such that

with the estimator $\hat{Z}(\lambda )=J({\hat{\lambda }}^{\ast }(\lambda ),{\hat{u}}_{\lambda })$. For purposes of efficiency, the spaces $\mathcal{U}$ and $\mathcal{V}$ can be replaced by some reduced basis approximation in (⁠5⁠).

Bayesian inference

Parameters $\lambda$ and measurements $Z(\lambda )$ can be considered as random variables. The relevance of this point of view is supported by their potential discrete natures and by the uncertainties and noise attached to them. Assume $\mathsf{p}$ (resp. $\mathsf{q}$) is the probability density followed by $\lambda$ (resp. $Z$). Bayesian inference provides the conditional density

where $\mathsf{p}(\lambda )$ is called the prior, i.e., the a priori distribution expected on $\lambda$; $\mathsf{q}(Z|\lambda )$ is the output likelihood given $\lambda$, i.e., the uncertainty on the output measurement or simulation. It results in an assessment of the $\lambda |Z$ distribution, known as posterior, that can be used as a new prior and so on, until uncertainties are judged satisfactory [⁠22⁠ D. Higdon, J. Gattiker, B. Williams and M. Rightley, Computer model calibration using high-dimensional output. J. Amer. Statist. Assoc.103, 570–583 (2008) , ⁠26⁠ M. C. Kennedy and A. O’Hagan, Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B Stat. Methodol.63, 425–464 (2001) ].

From a practical standpoint, a Markov Chain Monte Carlo approach can be used to simulate samples according to the distribution followed by $\lambda$, and a surrogate model – for instance relying on reduced bases – can be used to diminish the computational cost required to determine the output $Z$.

Selection of parameters

In order to make the approaches as efficient as possible, the parametric space $\Lambda$ must be reduced. A rather natural approach relies on variance decomposition, i.e. on the identification of subspaces within $\Lambda$ for which the covariance matrix $\mathbb{E}[Z^{\prime }\otimes Z^{\prime }]$ possesses the largest components; $Z^{\prime }=Z-\mathbb{E}(Z).$ This can be done by Sobol decomposition or Principal Component Analysis for linear models [⁠23⁠ B. Iooss and P. Lemaître, A review on global sensitivity analysis methods. In Uncertainty Management in Simulation-Optimization of Complex Systems, Oper. Res./Comput. Sci. Interfaces Ser. 59, Springer (2015) ]. Observe that in the vicinity of $\lambda$, the privileged most influential subspaces are given by the singular value decomposition of $d_{\lambda }Z\otimes d_{\lambda }Z$ in $T_{\lambda }\Lambda \times T_{\lambda }\Lambda$, the differential being computed by the adjoint method.

Sometimes, the parameters correspond to local characteristics of the model, such as material laws, and can be selected without involving the full resolution of the model. This is the case in Ortiz et al. [⁠24⁠ K. Karapiperis, L. Stainier, M. Ortiz and J. E. Andrade, Data-driven multiscale modeling in mechanics. J. Mech. Phys. Solids147, 104239, 16 (2021) , ⁠28⁠ T. Kirchdoerfer and M. Ortiz, Data-driven computational mechanics. Comput. Methods Appl. Mech. Engrg.304, 81–101 (2016) ], which rely on local measurements or simulations with a closest-point projection approach.

Filtering: From space conquest to cardiovascular modelling

The complementarity between first principle modelling and data analytics was pioneered in a unique manner by space conquest. This clever combination makes it possible to benefit from the predictive power of simple dynamic models and the ability to cope with noise and uncertainties within the environment; as a result, it offers the possibility of automated decisions when long transmission times allow for neither full real-time feedback on the system state nor efficient human steering. We describe the main associated ideas within a linear framework; cf. [⁠5⁠ A. Bensoussan, Filtrage optimal des systèmes linéaires. Dunod (1971) , ⁠6⁠ A. Bensoussan, Stochastic Control of Partially Observable Systems. Cambridge University Press, Cambridge (1992) , ⁠13⁠ B. d’Andréa Novel and M. Cohen de Lara, Commande linéaire des systèmes dynamiques. Modélisation. Analyse. Simulation. Commande. [Modeling. Analysis. Simulation. Control], Masson, Paris (1994) , ⁠30⁠ J.-L. Lions, Contrôle optimal de systèmes gouvernés par des équations aux dérivées partielles. Dunod, Paris; Gauthier-Villars, Paris (1968) ].

Filtering and optimal control

The above motivation was the main boost for the development of Kalman filtering, which is closely related to optimal control. Let $u(t)\in {\mathbb{R}}^n$ describe the state of the system at time $t\in [0,T]$ such that

where $\lambda \in {\mathbb{R}}^p$, $p<n$, stands for an unknown forcing contribution and $\xi$ for the uncertainty on the initial condition. Measurements $Z=Hu+\epsilon \in {\mathbb{R}}^m$ over $[0,T]$, with $m<n$, up to an error $\epsilon$, are available in order to help estimate the real trajectory, through the determination of $\lambda$ and $\xi$ such that

is infimised. Optimality is achieved for $\lambda (t)=L^{-1}{B}^{\top }p(t)$ and $\xi =N^{-1}p(0)$, where the adjoint state $p$ is a solution of the backward system in time

In order to avoid the difficulty of a two-end problem in $u$ and $p$, the optimal solution $u$ can be proven to decompose as $u=\hat{u}+Pp$, where $P$ is the operator solution from Riccati’s equation

The component $\hat{u}$ obeys the filtered dynamics

where $K=P{H}^{\top }M$ is Kalman’s gain; it reaches the optimal trajectory at time $t=T$, as $p(T)=0$. Beyond this Linear Quadratic setting, filtering can incorporate robust control, and adapt in many ways to the case of nonlinear systems (Extended Kalman Filter, Unscented Kalman Filter).

Hamilton–Jacobi–Bellman

Dynamic programming is of particular importance in order to proceed to nonlinear extensions. For every $q\in {\mathbb{R}}^n$ and $t\in [0,T]$, let us define the cost-to-come function

where the minimum is taken over controls $\tau \in [0,t]\mapsto \lambda (\tau )\in {\mathbb{R}}^p$ and trajectories $\tau \in [0,t]\mapsto u(\tau )\in {\mathbb{R}}^n$ with end-points $u(0)=u_0+\xi$ and $u(t)=q$. The cost function $V$ is a solution of the Hamilton–Jacobi–Bellman equation

in the sense of viscosity solutions, where

Observe that the optimality equations above read

Taking $V(u,0)=\frac{1}{2}|u-u_0{|}_N^2$ as an initial condition, let us assume the HJB equation admits a solution $V\in C^1(0,T;{\mathbb{R}}^n)$. Then, for all $t\in [0,T]$ the optimal command is given by

This provides the estimated dynamics

In the present linear setting, one has [⁠37⁠ P. Moireau, A discrete-time optimal filtering approach for non-linear systems as a stable discretization of the Mortensen observer. ESAIM Control Optim. Calc. Var.24, 1815–1847 (2018) ]

Stochastic perspective

Assume equation (⁠6⁠) is interpreted as astochastic differential equation, where $\lambda (t)$ and $\epsilon (t)$ are zero-mean independent Gaussian processes with covariance matrices $Q$ and $R$ respectively. The best mean square estimator $\hat{u}(t)=\mathbb{E}[u(t)|Z(t)]$ follows the same equation as in the previous paragraphs with $M=R^{-1}$ and $L=Q^{-1}$. The covariance matrix $P(t)=\mathbb{E}[(u-\hat{u})\otimes (u-\hat{u})]$ obeys Riccati’s equation.

Stability and control

Kalman’s gain achieves control optimality in the sense detailed above. Nevertheless, it can prove costly to determine, and difficult to access for distributed systems. As a matter of fact, some feedback terms acting as Lyapunov functions can suffice for practical purposes. Let us assume in the above that the gain $K$ is chosen in the form $K=\alpha H^{\top }\mathcal{M}$ with a symmetric definite positive matrix $\mathcal{M}$ and a coefficient $\alpha$ to determine. It follows that the error $e=u-\hat{u}$ satisfies

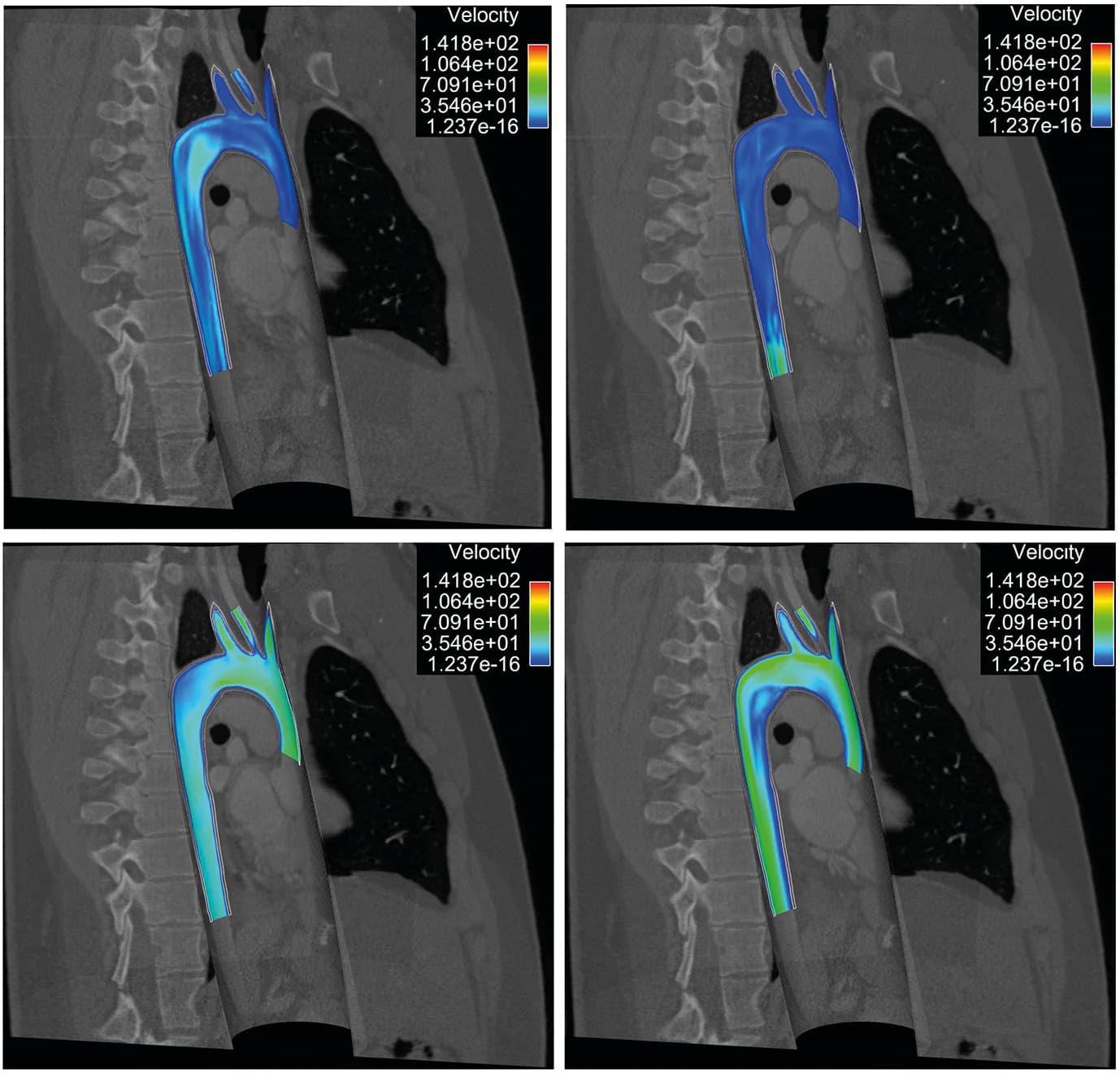
and can be made rapidly decreasing provided that $\lambda$ and $\epsilon$ remain moderate and $\alpha$ is taken sufficiently large. This approach has been implemented with multiple refinements by Moireau et al. [⁠39⁠ P. Moireau, D. Chapelle and P. Le Tallec, Filtering for distributed mechanical systems using position measurements: perspectives in medical imaging. Inverse Problems25, 035010, 25 (2009) ], comparing in-depth the displacement vs. velocity controls.

3.2 Solution space reduction

Reduced bases

The notion of reduced bases makes it possible to resolve the equations of the model in a low-dimensional subspace of solutions, rather than a large full finite element space for instance. It is reputed to go back to Rayleigh’s intuition, and is key to benefit from surrogate models that comply with the first physical principles, with high computational efficiency. It is particularly useful for high-dimensional models, as in Quantum Mechanics for instance. The approach has been made particularly popular by the work of Maday, Patera et al. [⁠32⁠ Y. Maday, Reduced basis method for the rapid and reliable solution of partial differential equations. In International Congress of Mathematicians. Vol. III, Eur. Math. Soc., Zürich, 1255–1270 (2006) ]. Some interesting challenges rise when handling highly nonlinear problems [⁠33⁠ Y. Maday, N. C. Nguyen, A. T. Patera and G. S. H. Pau, A general multipurpose interpolation procedure: the magic points. Commun. Pure Appl. Anal.8, 383–404 (2009) ]; it is particularly striking when contact mechanics is involved [⁠4⁠ A. Benaceur, Réduction de modèles en thermo-mécanique. PhD thesis, Paris Est University (2018) ], when structure preservation is concerned [⁠21⁠ J. Hesthaven and C. Pagliantini, Structure-preserving reduced basis methods for Hamiltonian systems with a nonlinear poisson structure (2018) , ⁠20⁠ P. Hauret, Multiplicative reduced basis for elasticity. submitted (2021) ], or when local accuracy is of particular importance [⁠46⁠ S. Riffaud, M. Bergmann, C. Farhat, S. Grimberg and A. Iollo, The DGDD method for reduced-order modeling of conservation laws. J. Comput. Phys.437, 110336, 19 (2021) ]. The efficiency of the method is well established when the Kolmogorov $n$-width of the solution manifold rapidly decreases as $n\to +\infty$; cf. [⁠2⁠ M. Barrault, Y. Maday, N. C. Nguyen and A. T. Patera, An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. C. R. Math. Acad. Sci. Paris339, 667–672 (2004) , ⁠8⁠ P. Binev, A. Cohen, W. Dahmen, R. DeVore, G. Petrova and P. Wojtaszczyk, Convergence rates for greedy algorithms in reduced basis methods. SIAM J. Math. Anal.43, 1457–1472 (2011) ].

Reduced order bases allow physical models to be interrogated (almost) as efficiently as data sets, making it possible to foster standard statistical learning methods [⁠1⁠ Y. S. Abu-Mostafa, M. Magdon-Ismail and H-T. Lin, Learning from Data. AMLbook.com (2012) , ⁠19⁠ T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning. 2nd ed., Springer Series in Statistics, Springer, New York (2009) ].

Parameterised-Background Data-Weak (PBDW) approach

Let

be the solution manifold for the “best-knowledge” model. It can be gradually approximated with diminishing errors by solutions of the model in reduced spaces ${\mathcal{R}}_1\subset \cdots \subset {\mathcal{R}}_N\subset \cdots \subset \mathcal{U}$.

The true solution $u^{\mathrm{true}}\in \mathcal{U}$ is unknown, but can be partially captured by experimental observations ${\ell }_m^{\mathrm{obs}}\in {\mathcal{U}}^{\ast }$ given as continuous linear forms of the solution: $1\le m\le M$. They provide the scalar quantities ${\mathbb{Z}}_m={\ell }_m^{\mathrm{obs}}(u^{\mathrm{true}})\in \mathbb{R}$. Let us write $(q_m)$ for the associated liftings satisfying $(q_m,v)={\ell }_m^{\mathrm{obs}}(v)$ for all $v\in \mathcal{U}$, where $(\cdot ,\cdot )$ denotes the inner product in the Hilbert space $\mathcal{U}$. It is imperative that the sensors be numerous enough ($N\le M$) to control the components of the reduced solution in the selected space ${\mathcal{R}}_M$; more specifically, one must have ${\mathcal{R}}_N\cap {\mathcal{U}}_M^{\perp }=\{0\}$ where ${\mathcal{U}}_M^{\perp }$ is orthogonal to ${\mathcal{U}}_M:=\mathrm{span}\{q_m,1\le m\le M\}$ in $\mathcal{U}$.

The PBDW method [⁠34⁠ Y. Maday, A. T. Patera, J. D. Penn and M. Yano, A parameterized-background data-weak approach to variational data assimilation: formulation, analysis, and application to acoustics. Internat. J. Numer. Methods Engrg.102, 933–965 (2015) , ⁠35⁠ Y. Maday, A. T. Patera, J. D. Penn and M. Yano, PBDW state estimation: noisy observations; configuration-adaptive background spaces; physical interpretations. In CANUM 2014 – 42e Congrès National d’Analyse Numérique, ESAIM Proc. Surveys 50, EDP Sci., Les Ulis, 144–168 (2015) , ⁠36⁠ Y. Maday and T. Taddei, Adaptive PBDW approach to state estimation: noisy observations; user-defined update spaces. SIAM J. Sci. Comput.41, B669–B693 (2019) ] determines the approximation $u_{N,M}$ of the solution $u^{\mathrm{true}}$ in the form

where

and the norm $\Vert {\eta }_{N,M}{\Vert }_{\mathcal{U}}$ is infimised. It boils down to finding $r_{M,N}\in {\mathcal{R}}_M$ and ${\eta }_{M,N}\in {\mathcal{U}}_M$ such that

This has been extended to a dynamic setting by Benaceur [⁠4⁠ A. Benaceur, Réduction de modèles en thermo-mécanique. PhD thesis, Paris Est University (2018) ], in collaboration with Patera. The method allows for a real-time correction of the solution, based upon available measurements. In case of noisy measurements, a regularisation is required and the following functional:

is infimised in order to compromise between the minimisation of the term $\Vert {\eta }_{N,M}{\Vert }_{\mathcal{U}}$ and the constraint (⁠7⁠), thus avoiding overfitting.

Data-driven reduced modelling

Each time the above reconstruction generates a prediction $u_{N,M}({\lambda }_k)$ for a given state ${\lambda }_k\in \Lambda$ of the system, the vector $u^{\mathrm{bk}}({\lambda }_k)$ can be replaced by $u_{N,M}({\lambda }_k)$ in the reduced basis for the system. This can be done by the dynamic reduced basis low rank adaption proposed by Peherstorfer and Wilcox [⁠42⁠ B. Peherstorfer and K. Willcox, Dynamic data-driven reduced-order models. Comput. Methods Appl. Mech. Engrg.291, 21–41 (2015) ].

Another point of view consists in fitting the expression of the operators involved in the best-knowledge model, when projected onto an a priori reduced basis. This idea was proposed by Peherstorfer and Wilcox [⁠43⁠ B. Peherstorfer and K. Willcox, Data-driven operator inference for nonintrusive projection-based model reduction. Comput. Methods Appl. Mech. Engrg.306, 196–215 (2016) ], who named it operator inference.

Finally, composite spaces can be constructed by the assembling of subdomains in which key driving parameters are retained and local reduced bases are adopted; coupling between subdomains can be performed via Lagrange multipliers, and the hidden parameters (for instance describing certain levels of damage within a structure) can be determined by statistical classification methods. Such approaches have been developed by Patera et al., and are called Port-Reduced Reduced-Basis Component (PR-RBC) methods; cf. [⁠7⁠ M. A. Bhouri and A. Patera, A two-level parameterized model-order reduction approach for time-domain elastodynamics. Comput. Methods Appl. Mech. Engrg.385, 114004 (2021) , ⁠16⁠ J. L. Eftang and A. T. Patera, Port reduction in parametrized component static condensation: approximation and a posteriori error estimation. Internat. J. Numer. Methods Engrg.96, 269–302 (2013) , ⁠48⁠ T. Taddei, J. D. Penn, M. Yano and A. T. Patera, Simulation-based classification: a model-order-reduction approach for structural health monitoring. Arch. Comput. Methods Eng.25, 23–45 (2018) ].

Tensor approximation of solutions

Since functions in separable form are dense in spaces of sufficiently regular functions, one can decompose the solution of the parameterised model problem in the form

by means of Proper Generalised Decompositions [⁠10⁠ F. Chinesta and P. Ladevèze (eds.), Separated Representations and PGD-Based Model Reduction. CISM International Centre for Mechanical Sciences. Courses and Lectures 554, Springer, Vienna (2014) ]. Of course, $\lambda$ can easily incorporate a wide variety of correction terms, so as to account for the current state of the system. This general philosophy has been widely popularised by Chinesta and Nouy; see [⁠9⁠ F. Chinesta, E. Cueto, E. Abisset-Chavanne, J. L. Duval and F. El Khaldi, Virtual, digital and hybrid twins: a new paradigm in data-based engineering and engineered data. Arch. Comput. Methods Eng.27, 105–134 (2020) , ⁠40⁠ A. Nouy, Proper generalized decompositions and separated representations for the numerical solution of high dimensional stochastic problems. Arch. Comput. Methods Eng.17, 403–434 (2010) ] and the references therein.

3.3 Multi-fidelity prediction and co-kriging

In many practical cases, several sources of information (simulation and measurement campaigns) provide predictions of various accuracies for the observables. Let $\Lambda$ be the parameter space under consideration. For every $1\le j\le J$, the $j$-th measurement or simulation campaign is performed at sampling points $D_j=({\lambda }_k^j{)}_{1\le k\le K_j}$ with the model $Z_j$ and provides data points ${\mathbb{Z}}_{j;k}=Z_j({\lambda }_k^j)$. The accuracy increases with $j$ and the most accurate forecast therefore corresponds to $j=J$.

Kriging

We set $j=1$, and recall the construction of the universal kriging ${\hat{Z}}_1(\lambda )$ as a non-biased approximation of $Z_1(\lambda )$ with minimum variance in the form

Universal kriging additionally assumes that $Z_1(\lambda )$ is a Gaussian process with unknown average of the form

and space correlation ${\sigma }_1^2{r}_1(\lambda ,{\lambda }^{\prime };\theta )$, where ${\sigma }_1$ is a variance scaling factor and $\theta$ a parameter of the space-correlation function $r_1$. The parameters ${\beta }_1$, ${\sigma }_1$ and $\theta$ can be determined through maximum likelihood. The non-biased minimum variance predictor is achieved for $w_1(\lambda )=C^{-1}(c(\lambda )+F^{\top }(F{C}^{-1}{F}^{\top }{)}^{-1}b(\lambda ))$, where the matrices $F,C$ are given by their components

and the vectors $c,b$ by

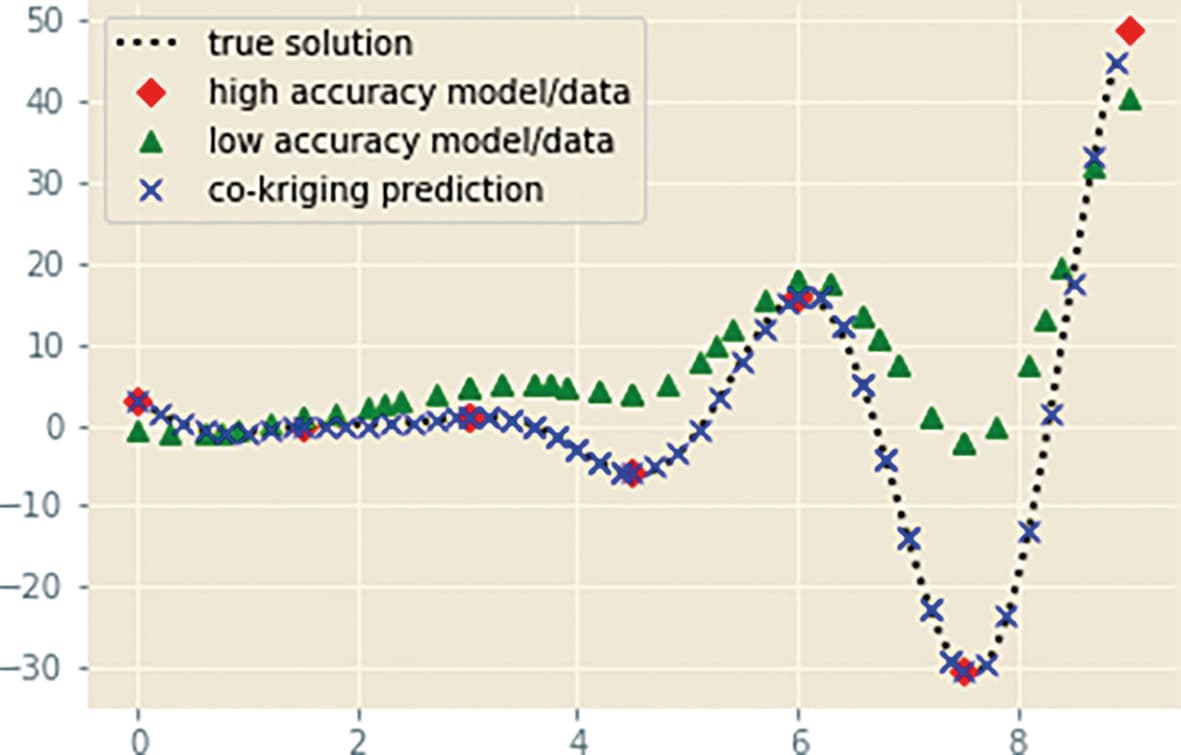
Recursive co-kriging

Co-kriging was pioneered by Kennedy and O’Hagan [⁠25⁠ M. C. Kennedy and A. O’Hagan, Predicting the output from a complex computer code when fast approximations are available. Biometrika87, 1–13 (2000) ]. The recursive multi-fidelity adaptation introduced by Le Gratiet and Garnier [⁠29⁠ L. Le Gratiet and J. Garnier, Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. Int. J. Uncertain. Quantif.4, 365–386 (2014) ] reads

where the following Gaussian processes are defined by their means and covariance matrices as

${\tilde{Z}}_j(\lambda )$ is a Gaussian process with distribution

where $Z^{(j)}=(Z_1(D_1),\dots ,Z_j(D_j))$ and ${\mathbb{Z}}^{(j)}=({\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_j)$.

The combined use of reduced models, full accuracy simulations and measurements clearly allow for very efficient and accurate surrogate models. The co-kriging above, further developed in [⁠44⁠ P. Perdikaris, D. Venturi, J. O. Royset and G. E. Karniadakis, Multi-fidelity modelling via recursive co-kriging and Gaussian–Markov random fields. Proc. R. Soc. A.471 (2015) ], has the huge advantage of recursiveness and as a result, a very accessible computational cost.

3.4 Physics-Informed Neural Network

Neural networks have had great success with classification problems, together with Support Vector Machines for instance [⁠1⁠ Y. S. Abu-Mostafa, M. Magdon-Ismail and H-T. Lin, Learning from Data. AMLbook.com (2012) ]. They generate functions that are dense among continuous functions (cf. Cybenko [⁠12⁠ G. Cybenko, Approximation by superpositions of a sigmoidal function. Math. Control Signals Systems2, 303–314 (1989) ]), and conciliate smoothness with the ability to represent thresholds quite accurately. Fitting can be performed by a back descent gradient inspired by optimal control techniques. Furthermore, robust and powerful Python libraries, like Tensor Flow, are freely available.

Physics-Informed Neural Networks were introduced by Raissi, Perdikaris and Karniadakis [⁠45⁠ M. Raissi, P. Perdikaris and G. E. Karniadakis, Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys.378, 686–707 (2019) ]. They combine the statistical learning of the solution, say $u$ on the space-time domain $[0,T]\times \Omega$ sampled on points $(t^n,x_i)$ as $u_i^n$, under the penalised constraint that $u$ is expected to resolve a partial differential equation of the form $\mathcal{A}(u)=0$ in $[0,T]\times \Omega$. This reads as the infimisation

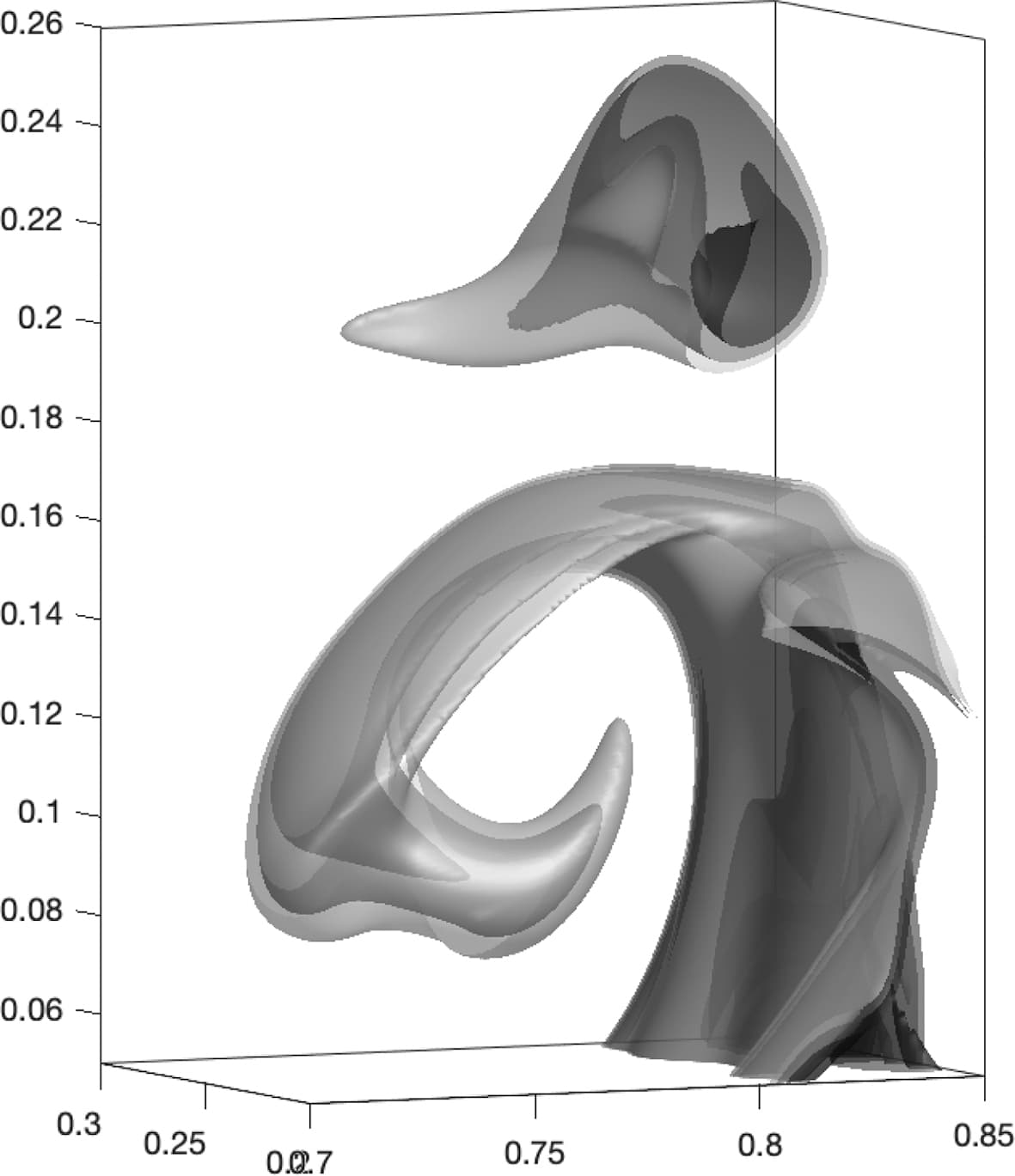
which is close to (⁠1⁠) when $J(\lambda ,u)=u$. A Bayesian approach can be used to identify the parameters from the model, as developed in [⁠49⁠ L. Yang, X. Meng and G. E. Karniadakis, B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys.425, 109913, 23 (2021) ]. Lucor et al. have developed the approach for the thermo-mechanical simulation of an incompressible viscous flow [⁠31⁠ D. Lucor, A. Agrawal and A. Sergent, Physics-aware deep neural networks for surrogate modeling of turbulent natural convection, preprint, arXiv:2103.03565 (2021) ]; cf. Figures ⁠5⁠ and ⁠6⁠.

4 Conclusion

The combined use of first principle models and data analytics is an avenue for predictive sciences. It is a privileged way to synergise the modelling knowledge present in simulation software with the relevance of available data, while guaranteeing a high level of predictiveness in operation. Beyond the necessity of a growing mathematical toolbox to handle problems of optimal control with extreme efficiency, several challenges are implied: (i) the necessity of developing porosity at the interface between competences (numerical analysis, optimal control and automatism, high performance computing, statistics, computer sciences), (ii) the need for integrated development environments, with a role to play in the question of open software, and (iii) data protection, as data becomes an outstanding source of value.

Acknowledgements I thank Krzysztof Burnecki for the kind invitation to write this article. I am indebted to Philippe Moireau, Amina Benaceur, Didier Lucor and Anne Sergent for providing the illustrations displayed in Section ⁠3⁠, and for our exchanges on the corresponding advances. The promotion of Digital Twins also owes thanks to my colleagues from the EU-MATHS-IN Industrial Core Team, with special thanks to Dirk Hartman, Zoltán Horváth, Wil Schilders, Cor van Kruijsdijk and Hubert Tardieu. In this regard, Section ⁠1⁠ presents several collective statements.

Patrice Hauret is research director at Michelin, head of Modelling, Data and Physical Analysis. He has held several managing R & D positions in the development of innovative tires and technologies. He holds a Ph.D. in Applied Mathematics from the École Polytechnique and was a postdoctoral fellow at the California Institute of Technology. He completed the French Habilitation to Direct Research (HDR).His scientific contributions are mainly in the fields of Elastodynamics, Approximation Methods, Multi-Scale and Domain Decomposition Methods. He was awarded the École Polytechnique Ph.D. Award in 2005 and the Felix Klein Prize from the European Mathematical Society in 2016. He is a member of several advisory boards committed to open innovation and to the economic impact of mathematical sciences in France and Europe. patrice.hauret@gmail.com

1. ¹

   ATOS, Bosch, Dassault Aviation, EcoMT, EY, Michelin, NORS Group, Shell, Siemens

2. ²

   ec.europa.eu/info/horizon-europe_en

References

1. Y. S. Abu-Mostafa, M. Magdon-Ismail and H-T. Lin, Learning from Data. AMLbook.com (2012)
2. M. Barrault, Y. Maday, N. C. Nguyen and A. T. Patera, An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. C. R. Math. Acad. Sci. Paris339, 667–672 (2004)
3. P. Bauer, B. Stevens and W. Hazeleger, A digital twin of earth for the green transition. Nature Climate Change11, 80–83 (2021)
4. A. Benaceur, Réduction de modèles en thermo-mécanique. PhD thesis, Paris Est University (2018)
5. A. Bensoussan, Filtrage optimal des systèmes linéaires. Dunod (1971)
6. A. Bensoussan, Stochastic Control of Partially Observable Systems. Cambridge University Press, Cambridge (1992)
7. M. A. Bhouri and A. Patera, A two-level parameterized model-order reduction approach for time-domain elastodynamics. Comput. Methods Appl. Mech. Engrg.385, 114004 (2021)
8. P. Binev, A. Cohen, W. Dahmen, R. DeVore, G. Petrova and P. Wojtaszczyk, Convergence rates for greedy algorithms in reduced basis methods. SIAM J. Math. Anal.43, 1457–1472 (2011)
9. F. Chinesta, E. Cueto, E. Abisset-Chavanne, J. L. Duval and F. El Khaldi, Virtual, digital and hybrid twins: a new paradigm in data-based engineering and engineered data. Arch. Comput. Methods Eng.27, 105–134 (2020)
10. F. Chinesta and P. Ladevèze (eds.), Separated Representations and PGD-Based Model Reduction. CISM International Centre for Mechanical Sciences. Courses and Lectures 554, Springer, Vienna (2014)
11. CMI, Etude de l’impact socio-économique des mathématiques en france [CMI, A study of the soci-economical impact of mathematics in France] (2015)
12. G. Cybenko, Approximation by superpositions of a sigmoidal function. Math. Control Signals Systems2, 303–314 (1989)
13. B. d’Andréa Novel and M. Cohen de Lara, Commande linéaire des systèmes dynamiques. Modélisation. Analyse. Simulation. Commande. [Modeling. Analysis. Simulation. Control], Masson, Paris (1994)
14. Deloitte, Measuring the economic benefits of mathematical sciences research in the UK. Deloitte (2012)
15. Deloitte, Mathematical sciences and their value for the dutch economy. Deloitte (2014)
16. J. L. Eftang and A. T. Patera, Port reduction in parametrized component static condensation: approximation and a posteriori error estimation. Internat. J. Numer. Methods Engrg.96, 269–302 (2013)
17. EU-MATHS-IN Industrial Core Team, Modelling, simulation and optimization in a data rich environment: a window of opportunity to boost innovation in Europe. Foundation EU-MATHS-IN, European Service Network of Mathematics for Industry (2018)
18. D. Hartmann and H. Van der Auweraer, Digital twins. Siemens. arXiv:2001.09747 (2019)
19. T. Hastie, R. Tibshirani and J. Friedman, The Elements of Statistical Learning. 2nd ed., Springer Series in Statistics, Springer, New York (2009)
20. P. Hauret, Multiplicative reduced basis for elasticity. submitted (2021)
21. J. Hesthaven and C. Pagliantini, Structure-preserving reduced basis methods for Hamiltonian systems with a nonlinear poisson structure (2018)
22. D. Higdon, J. Gattiker, B. Williams and M. Rightley, Computer model calibration using high-dimensional output. J. Amer. Statist. Assoc.103, 570–583 (2008)
23. B. Iooss and P. Lemaître, A review on global sensitivity analysis methods. In Uncertainty Management in Simulation-Optimization of Complex Systems, Oper. Res./Comput. Sci. Interfaces Ser. 59, Springer (2015)
24. K. Karapiperis, L. Stainier, M. Ortiz and J. E. Andrade, Data-driven multiscale modeling in mechanics. J. Mech. Phys. Solids147, 104239, 16 (2021)
25. M. C. Kennedy and A. O’Hagan, Predicting the output from a complex computer code when fast approximations are available. Biometrika87, 1–13 (2000)
26. M. C. Kennedy and A. O’Hagan, Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B Stat. Methodol.63, 425–464 (2001)
27. M. Kerremans, D. Cearley, A. Velosa and M. Walker, Top 10 strategic technology trends for 2019: digital twins.www.gartner.com/en/documents/3904569/top-10-strategic-technology-trends-for-2019-digital-twin, Gartner (2019)
28. T. Kirchdoerfer and M. Ortiz, Data-driven computational mechanics. Comput. Methods Appl. Mech. Engrg.304, 81–101 (2016)
29. L. Le Gratiet and J. Garnier, Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. Int. J. Uncertain. Quantif.4, 365–386 (2014)
30. J.-L. Lions, Contrôle optimal de systèmes gouvernés par des équations aux dérivées partielles. Dunod, Paris; Gauthier-Villars, Paris (1968)
31. D. Lucor, A. Agrawal and A. Sergent, Physics-aware deep neural networks for surrogate modeling of turbulent natural convection, preprint, arXiv:2103.03565 (2021)
32. Y. Maday, Reduced basis method for the rapid and reliable solution of partial differential equations. In International Congress of Mathematicians. Vol. III, Eur. Math. Soc., Zürich, 1255–1270 (2006)
33. Y. Maday, N. C. Nguyen, A. T. Patera and G. S. H. Pau, A general multipurpose interpolation procedure: the magic points. Commun. Pure Appl. Anal.8, 383–404 (2009)
34. Y. Maday, A. T. Patera, J. D. Penn and M. Yano, A parameterized-background data-weak approach to variational data assimilation: formulation, analysis, and application to acoustics. Internat. J. Numer. Methods Engrg.102, 933–965 (2015)
35. Y. Maday, A. T. Patera, J. D. Penn and M. Yano, PBDW state estimation: noisy observations; configuration-adaptive background spaces; physical interpretations. In CANUM 2014 – 42e Congrès National d’Analyse Numérique, ESAIM Proc. Surveys 50, EDP Sci., Les Ulis, 144–168 (2015)
36. Y. Maday and T. Taddei, Adaptive PBDW approach to state estimation: noisy observations; user-defined update spaces. SIAM J. Sci. Comput.41, B669–B693 (2019)
37. P. Moireau, A discrete-time optimal filtering approach for non-linear systems as a stable discretization of the Mortensen observer. ESAIM Control Optim. Calc. Var.24, 1815–1847 (2018)
38. P. Moireau, C. Bertoglio, N. Xiao, C. A. Figueroa, C. A. Taylor, D. Chapelle and J.-F. Gerbeau, Sequential identification of boundary support parameters in a fluid-structure vascular model using patient image data. Biomechanics and Modeling in Mechanobiology12, 475–496 (2012)
39. P. Moireau, D. Chapelle and P. Le Tallec, Filtering for distributed mechanical systems using position measurements: perspectives in medical imaging. Inverse Problems25, 035010, 25 (2009)
40. A. Nouy, Proper generalized decompositions and separated representations for the numerical solution of high dimensional stochastic problems. Arch. Comput. Methods Eng.17, 403–434 (2010)
41. NSF and WTEC, www.nsf.gov/pubs/reports/sbes_final_report.pdf; www.wtec.org/sbes/SBES-GlobalFinalReport.pdf.
42. B. Peherstorfer and K. Willcox, Dynamic data-driven reduced-order models. Comput. Methods Appl. Mech. Engrg.291, 21–41 (2015)
43. B. Peherstorfer and K. Willcox, Data-driven operator inference for nonintrusive projection-based model reduction. Comput. Methods Appl. Mech. Engrg.306, 196–215 (2016)
44. P. Perdikaris, D. Venturi, J. O. Royset and G. E. Karniadakis, Multi-fidelity modelling via recursive co-kriging and Gaussian–Markov random fields. Proc. R. Soc. A.471 (2015)
45. M. Raissi, P. Perdikaris and G. E. Karniadakis, Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys.378, 686–707 (2019)
46. S. Riffaud, M. Bergmann, C. Farhat, S. Grimberg and A. Iollo, The DGDD method for reduced-order modeling of conservation laws. J. Comput. Phys.437, 110336, 19 (2021)
47. Digital twins – explainer video. youtu.be/ObGhB9CCHP8, Siemens AG (2019)
48. T. Taddei, J. D. Penn, M. Yano and A. T. Patera, Simulation-based classification: a model-order-reduction approach for structural health monitoring. Arch. Comput. Methods Eng.25, 23–45 (2018)
49. L. Yang, X. Meng and G. E. Karniadakis, B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys.425, 109913, 23 (2021)