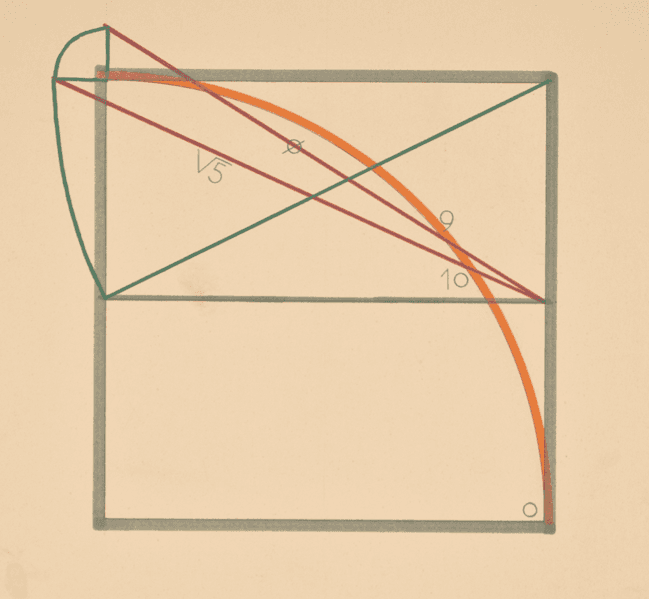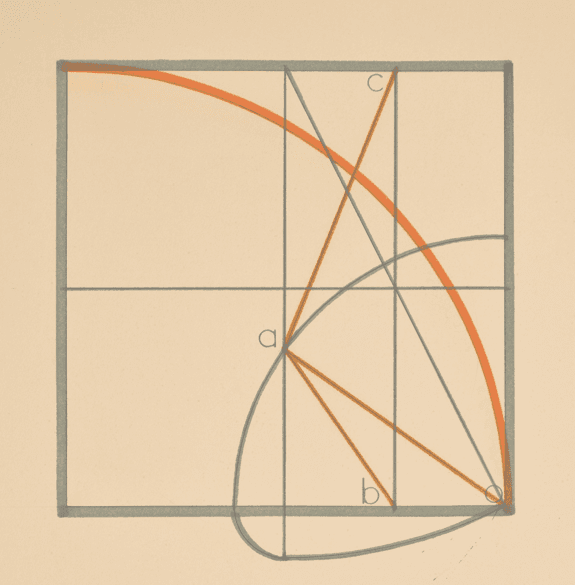The geometric theorems of Almada Negreiros

José de Almada Negreiros (São Tomé and Príncipe, 1893 – Lisbon, 1970) was a key figure of 20th century Portuguese culture, in both visual arts and literature. His visual work went through several stages: starting with mostly figurative work, he became increasingly closer to geometric abstractionism, which he came to adopt completely in 1957, in four works displaying simple geometric figures in black and white.

This progressive change in style was not just the result of an aesthetic choice, but also the consequence of a way of thinking about the relationship between art and geometry. In fact, Almada – this was his own choice of name – believed in a universal geometric system, underlying all visual art, throughout time. He called his system “The Canon”.

This belief in the universality of mathematics as a foundation for art may remind us of Le Corbusier’s belief that his Modulor system, based on three simple concepts – unit, the double and the golden section – would tap into an abstract and universal form of beauty. Other authors of his time, such as Matila Ghyka, also developed similar lines of thought.

Almada’s system involved several geometrical elements, such as rectangles with known proportions – such as $\sqrt{2},\phi$ (the golden rectangle), $\sqrt{3},2,\sqrt{5},\sqrt{\phi }$ – divisions of the circle into equal parts, and the golden angle. These were used by Almada to describe and understand artistic artifacts, and were seen as a sign that there was a collection of such constructions that was used, consciously or unconsciously, by artists of all styles and origins.

However, also like Le Corbusier, Almada also actually proved mathematical statements. In his book Le Modulor [⁠2⁠ Le Corbusier, Le Modulor. Birkhäuser Architecture, 2000. , p. 37] Le Corbusier suggests a construction for a right angle, placed within a rectangle, according to certain rules. The construction (which is not presented in full clarity and detail) actually does lead to an approximate right angle.

Almada goes much farther in his speculative geometry. In two collections of drawings as well as some artist’s notebooks, comprising more than a hundred completed works as well as many additional sketches, he presents constructions of a geometric nature which can rightly be regarded as artworks, but which are at the same time geometric results related to the elements of the Canon, showing their intrinsic proximity. Figures ⁠2⁠ and ⁠3⁠ present two examples from the collection “Language of the square”, a set of about forty-five finished drawings on paper, $50\times 70$ cm.

Both drawings can be regarded as protocols for geometric constructions, both starting with a square divided in two equal parts by a horizontal line, with an inscribed quarter circle. The construction in Figure ⁠2⁠ leads to two red lines, marked $\sqrt{5}$ and $\phi$, indicating that these lines are diagonals of rectangles with those proportions, and sides parallel to the sides of the square.

It is not difficult to verify the correctness of the proportions. If we take half of the side of the square as our unit measure, then, by the Pythagorean Theorem, the green diagonal measures $\sqrt{5}$, and as this measure is transported, by compass, to the top side of the square, we do obtain a rectangle with this proportion.

The small green horizontal line would then measure $\sqrt{5}-2$, and as we add it to half the square, we get a length of $1+\sqrt{5}-2=\sqrt{5}-1$. The proportion of the rectangle having as diagonal the red line marked $\phi$ would then be

The numbers 9 and 10 on the right refer to the divisions of the circle into 9 and 10 parts, which are achieved by the intersection of the red lines with the circle arc. As it happens, the proportions of the rectangles are precise, but the divisions of the circle are not: they represent very good approximations, each having an error of about 0.7 %. In the book [⁠4⁠ P. J. Freitas and S. P. Costa, Almada Negreiros and the geometric canon. J. Math. Arts9, 27–36 (2015) ], the authors present a few more analyses of this type concerning about 30 of Almada’s drawings.

In Figure 3, a similar but more intricate construction leads to four points marked a, b, c and o, and three lengths, which Almada interprets as follows:

This is again a reference to the division of the circle into equal parts. In this case, the 10th part is exact, the 14th part has an error of 1 % and the 9th part has an astonishingly tiny error of 0.001 %.⁠¹⁠The article [⁠3⁠ P. J. Freitas, Almada Negreiros and the regular nonagon. Recreat. Math. Mag. 39–51 (2015) ] compares the approximation for the 9th part of the circle achieved by this construction with that of other constructions and concludes this is one is the best of all those analysed.

In the history of mathematics, the problem of dividing the circle into n equal parts with straightedge and compass has a respectable place. Thinking about prime values of n, it has known since ancient Greece that it is possible to divide the circle into 3 and 5 parts, but no method was found for 7, 11 or 13 parts. It was Gauss, in 1796, who proved that it was possible to divide the circle into 17 parts, a result that came to be included in Section VII of Disquisitiones Arithmeticae.⁠²⁠There is an anecdote that Gauss was so pleased by this result that he requested that a regular heptadecagon be inscribed on his tombstone. The stonemason declined, stating that the difficult construction would essentially look like a circle. Eventually, he found a sufficient condition for the division into n parts, and stated that this condition should also be necessary. In 1837, Pierre Wantzel proved the necessity, leading to the result that became known as the Gauss–Wantzel theorem.

Going back to Almada’s constructions, we note that 7 is not a Fermat prime, and $9=3\times 3$ (3 is a Fermat prime that occurs twice in the factorization). Therefore, a circle cannot be divided precisely into 9 and 14 parts using only straightedge and compass.

The purpose of these constructions is mainly to show that the various elements of Almada’s Canon have a natural and harmonious relationship amongst themselves, which is revealed by the elegance and simplicity of the geometric constructions he presents. Thus, the aim is primarily symbolic and philosophical rather than mathematical. Nevertheless, these drawings also present original constructions for the divisions of the circle and for producing rectangles with a given proportion, so in fact, they represent original mathematical results, even though some of them are approximate.

Many more drawings exist, some of them leading to general statements which one might regard as theorems, if it weren’t for the fact that they represent approximations. One of these statements is

The meaning of this equality is that 2 chords of the 9th part of the circle plus a chord of the 10th part will equal the diameter of the circle (two times the radius). The first side of the equation is actually equal to $1.986r$, an error of 0.7 %.

The presence of the numbers 9 and 10 in this equality (and in many geometric constructions) is not fortuitous. Almada believed there was a special connection between these two numbers, which he called the “Relation 9/10” and strove to seek for them and to connect them with other elements of his Canon. This is also the reason for the presence of these numbers in Figures ⁠2⁠ and ⁠3⁠.

The statement above is used in an approximate construction for the pentagram (another of Almada’s favourite figures, because of its relation to the Pythagoreans). The construction starts with a circle with two elements marked: a diameter and a 9th part, measured from one of the extremes of the diameter. In Figure ⁠4⁠, the 9th part is the arc AP₉, on the left, and the diameter is marked AB.

The construction now goes as follows. The arc of a circle centred at A is drawn from the point P₉ to the diameter, marking point D, through which one of the lines of the pentagram is drawn: CE, perpendicular to AB. This point D is now the centre of the half circle AF. Point F now determines a new arc of a circle with centre B, yielding points G and H, through which the remaining lines of the pentagram are defined.

According to this construction, lines AD and DF are chords of the 9th part of the circle, and line FB is the chord of the 10th part (which is the chord of both arcs BG and GH). These three lines add up to a diameter, which illustrates the previous equation, connecting it to the pentagram.

We emphasize that this is not an accurate construction – it is actually impossible for it to be accurate, according to Gauss–Wantzel’s theorem, since otherwise the 9th part of the circle would be constructible, if we could start with a pentagon and extract point P₉ from it.

The fact that some of these results are approximations, and that these appear among exact results with no distinction, is actually quite revealing of Almada’s methods. We have reason to believe that Almada didn’t actually compute the exact measures of the elements he claimed to produce, but probably only checked them visually, using instruments of measure or other elements of comparison. So, his way of establishing geometric results is not the same as the one used by mathematicians. And even though Almada was aware that some of his results were approximate, he stuck to them and never distinguished between exact and approximate ones. This was probably because he was more interested in the visual aspects of such results, and for this effect, some approximations are acceptable.

One of his last artworks, which can be considered his geometric legacy and a summary of many of his statements on this subject, is the mural Começar (To begin, 1968), which is located in the main hall of the building of the Gulbenkian Foundation in Lisbon. It is a very intricate collection of lines and circles, inscribed in stone, with dimensions $12.87\times 2.31$ m (see Figure ⁠5⁠).

The mural is usually divided into five parts. The first one displays the pentagram with the construction presented in Figure ⁠4⁠ as the main motif. Then, we find a 16-point star, which is an allusion to a drawing by Leonardo da Vinci appearing (apparently by mistake) in Geneva’s codex of Luca Pacioli’s Divina Proportione. The central element is again a pentagram, which Almada associates to a coin, minted by Portugal’s first king, which is set in the midst of many other constructions that Almada used to study some 15th century Portuguese paintings. The right part of the mural presents references to the Minoan civilization and to a medieval poem associated with a guild of cathedral stonemasons. There is a virtual guided tour at gulbenkian.pt/almada-comecar/en/ where the reader can find more detailed information about this mural. However, what we wish to point out with these brief remarks is that Almada’s geometry is truly an effort to unite all art and all cultures.

A thorough study of the geometric works in Almada’s estate has been undertaken, in a collaboration between Simão Palmeirim and the author; some of its results can be found in [⁠4⁠ P. J. Freitas and S. P. Costa, Almada Negreiros and the geometric canon. J. Math. Arts9, 27–36 (2015) ]. We hope that this study can bring to light not only the remarkable visual aspects of Almada’s geometric work, but also the mathematics behind it, which not only yield new geometric results, but also represent a powerful statement about the author’s thought regarding geometry and art.

Acknowledgements

We wish to thank the family of Almada Negreiros for allowing us to study his estate and for giving permission to use the reproductions in Figures ⁠1⁠, ⁠2⁠ and ⁠3⁠. This study was done within the scope of project Modernismo Online, Universidade Nova de Lisboa (www.modernismo.pt), which aims to collect in digital form the heritage of Portuguese Modernism.

Figure ⁠5⁠ is by Manuel V. Botelho (commons.wikimedia.org/w/index.php?curid=35070536), CC BY-SA 4.0 (creativecommons.org/licenses/by-sa/4.0/).

The author is supported by FCT, I.P., through Project UID/HIS/00286/2019.

Pedro J. Freitas has a PhD in mathematics and works in the Department of History and Philosophy of Sciences in the University of Lisbon. He is a member of the Interuniversity Center for the History and Philosophy of Sciences. His teaching and research are mainly related to the history of mathematics, recreational mathematics and relations between mathematics and art. He is also involved in mathematical outreach. pjfreitas@fc.ul.pt

1. ¹

   The article [⁠3⁠ P. J. Freitas, Almada Negreiros and the regular nonagon. Recreat. Math. Mag. 39–51 (2015) ] compares the approximation for the 9th part of the circle achieved by this construction with that of other constructions and concludes this is one is the best of all those analysed.

2. ²

   There is an anecdote that Gauss was so pleased by this result that he requested that a regular heptadecagon be inscribed on his tombstone. The stonemason declined, stating that the difficult construction would essentially look like a circle.

References

1. S. P. Costa and P. J. Freitas, Livro de Problemas de Almada Negreiros, Leituras em Matemática, 14. Portuguese Mathematical Society (2015)
2. Le Corbusier, Le Modulor. Birkhäuser Architecture, 2000.
3. P. J. Freitas, Almada Negreiros and the regular nonagon. Recreat. Math. Mag. 39–51 (2015)
4. P. J. Freitas and S. P. Costa, Almada Negreiros and the geometric canon. J. Math. Arts9, 27–36 (2015)