The Argentine mathematician has been a leading figure in the development of partial differential equations in the last 50 years and was awarded with the 2023 Abel Prize “for his seminal contributions to regularity theory for nonlinear partial differential equations including free-boundary problems and the Monge–Ampère equation.” His contributions are not limited to these fields, they include problems in fluid mechanics, optimal transportation, non-local operators, homogenization, and other topics with important connections with other sciences. In a series of landmark contributions Luis used brilliant geometric insights together with ingenious analytical tools to study areas of nonlinear mathematics that were barely explored some decades ago and are now in full bloom. This text combines a description of Luis’s main contributions with a glimpse into his life and personality.
Introduction
The Norwegian Academy of Sciences and Letters has awarded the 2023 Abel Prize to Luis Ángel Caffarelli, a mathematician from the University of Texas at Austin, USA. The prize is generally considered the mathematical equivalent of the Nobel Prizes of the Royal Swedish Academy of Sciences and has been awarded since 2003 to individuals who have made “outstanding scientific work in the field of mathematics.” The citation about Caffarelli’s work specifically says: “for his seminal contributions to regularity theory for nonlinear partial differential equations including free-boundary problems and the Monge–Ampère equation.” But his contributions are not limited to the already mentioned fields, they also include problems in fluid mechanics, optimal transportation, calculus of variations, non-local operators, homogenization, and other topics that have important connections with other sciences. According to the American Mathematical Society: “Some of his most significant contributions are the regularity of free boundary problems and solutions to nonlinear elliptic partial differential equations, optimal transportation theory, and, more recently, results in the theory of homogenization.”1Notices of the AMS: https://www.ams.org/notices/201404/rnoti-p393.pdf. See also: https://www.ams.org/journals/notices/201808/rnoti-p1019.pdf
Luis Caffarelli, photo from the University of Texas at Austin, USA.
©All rights reserved.
His work on the regularity of free boundaries has opened remarkable ways for geometric methods to play a relevant role in the analysis of equations. Free boundary problems appear naturally in very different contexts, ranging from fluid filtration, elasticity, optimal strategies in finance, economics, metal industry, interacting particle systems in physics, to topics in biology and ecology.
Luis Caffarelli receives the Abel Prize from King Harald of Norway.
©Alf Simensen – NTB / The Abel Prize
As Norwegian mathematician Helge Holden, chair of the Abel Committee, noted: “Combining brilliant geometric insight with ingenious analytical tools” to pioneer a field of mathematics that was barely explored four decades ago. And, later, Holden added: “Caffarelli’s theorems have radically changed our understanding of classes of nonlinear partial differential equations with wide applications. The results go to the core of the matter, the techniques show at the same time virtuosity and simplicity, and cover many different areas of mathematics and its applications.” Many other prominent mathematicians have pondered on his gifts. Francesco Maggi, a colleague of Luis at the University of Texas at Austin, said: “Forty years after these papers appeared, we have digested them, and we know how to do some of these things more efficiently. But when they appeared back in the day, in the 80s, these were alien mathematics.”2Quoted from the article in New Scientist, “Mathematician wins Abel Prize for solving equations with geometry,” 22 March 2023, by Alex Wilkins. Many of us have often wondered about his unexpected insights combined with skillful use of analytical tools… plus a touch of deceivingly simple geometry.
Biographic highlights
Luis Caffarelli was born in 1948 in Buenos Aires, Argentina, where he got his PhD degree in mathematics in 1972. He has lived in the US since 1973. His early American years were spent in Minnesota, a beautiful state of the Midwest with quite extreme weather that has been home to brilliant science during the 20th century. The University of Minnesota, where he taught, brings back very fond memories to many Spanish scientists of the generation that began their research careers in the 1970s, especially experts in economics, medicine, and mathematics.
Luis rose to worldwide fame at the end of that decade because of his surprising work on the regularity of the so-called free boundaries, nowadays familiar to a wide scientific public largely thanks to his work. We will see a brief description of these concepts later on. Luis surprised everyone in the mathematical community with the article “The regularity of free boundaries in higher dimensions,” published in 1977 [4 L. A. Caffarelli, The regularity of free boundaries in higher dimensions. Acta Math. 139, 155–184 (1977) ]. This very remarkable work laid the basis of his future fame. It is where his ingenuity in mixing partial differential equations (PDEs) and geometry first manifested. The novelty and brilliance of his treatment of the obstacle problem is already a classic reference in pure and applied mathematics, a paradigmatic example of what we call free boundary problems. It is worth highlighting the contributions that Luis has made to the Stefan problem, which mathematically describes solid–liquid phase transitions. It models, among other applications, the evolution of the ice–water system with its fine separation interface, a topic that reaches the general public through the process of melting glaciers or ice cubes melting in water. The substances in the applications need not be ice and water. Thus, in the continuous casting process employed in the steel industry, the free boundary problem concerns the determination of the solid–liquid steel interface.
A second work by Luis that was to have a great impact dates back to 1982. It arose as the result of a collaboration with Robert Kohn and Louis Nirenberg and deals with fluids. The paper, “Partial regularity of suitable weak solutions of the Navier–Stokes equation,” was published in 1982 [1 L. Caffarelli, R. Kohn and L. Nirenberg, Partial regularity of suitable weak solutions of the Navier–Stokes equations. Comm. Pure Appl. Math. 35, 771–831 (1982) ]. The work was carried out during Caffarelli’s first period as a professor at the Courant Institute of Mathematical Sciences in New York. Louis Nirenberg, also an Abel Prize winner (in 2015), was his supporter in those years and remained his friend for life. Years went by and this beautiful result, the theorem known as CKN in honor of its authors, continues to stand out as the last great contribution made in the study of regularity of solutions of the Navier–Stokes equations for viscous fluids. Here we are talking about one of the famous seven “Millennium Prize Problems” of the Clay Mathematics Institute.
We have specifically cited these two works by Luis because the work of great mathematicians is often linked to some influential articles containing far-reaching results, or to books presenting deep theories. The 1980s were a prodigious time for Caffarelli. A cascade of articles with various coauthors established him as the best worldwide representative of the legacy of David Hilbert (circa 1900) and Ennio de Giorgi (circa 1960) on “how to study the regularity inherent in the solutions of the problems of the calculus of variations.” Luis added to the program of the great Ennio the study of free boundary problems that we will deal with shortly. These problems had challenged the best experts during the 1960s and 1970s due to their intricate combination of difficulties from analysis and geometry.
Luis is one of the world’s leading experts in the field of nonlinear partial differential equations. Partial differential equations have been studied for hundreds of years and describe almost every sort of physical process, ranging from fluids and combustion engines to financial models. Caffarelli’s most important work concerns nonlinear PDEs, which describe complex relationships between the variables of the system and their derivatives. The influence of geometrical thinking permeates his highly original contributions.
From 1986 to 1996 Luis was a permanent professor at the Institute for Advanced Study, Princeton, an institution famous for legendary figures such as Albert Einstein, John von Neumann, and Robert Oppenheimer. After that, Luis went back as a professor to the Courant Institute, and finally moved in 1997 to the University of Texas at Austin, where he is still a professor (Sid W. Richardson Foundation Regents’ Chair in Mathematics No. 1). Social recognition for him and his work has been continuous and growing. Since 1991 he has been an outstanding scientist in the US and a member of the National Academy of Sciences. In addition, a series of international awards came to recognize the impact of his scientific contributions: in the present century, the Rolf Schock Prize, from the Royal Swedish Academy of Sciences (2005); the Leroy P. Steele Prize “for lifetime achievement” from the American Mathematical Society (AMS, 2009); the very prestigious Wolf Prize (2012); the Solomon Lefschetz Medal, from the Mathematical Council of the Americas (2013); again, a Leroy P. Steele Prize, this time “for seminal contribution to research” for the landmark article published in 1982 with Robert Kohn and Louis Nirenberg, from AMS (2014); as well as the Shaw Prize in Mathematics, which is considered the “Asian Nobel Prize” (2018). A brief glimpse of his greatest scientific achievements will be shown in the next section.
Luis Caffarelli in younger years.
©All rights reserved.
Mathematical area and contributions in some detail
Caffarelli’s scientific work developed inside the mathematical field of nonlinear partial differential equations (NL PDEs), but it is important to highlight the interest that Luis showed for the connections between nonlinear PDEs and other sciences since his pre-doctoral studies. We reproduce some fragments of the citation for the Abel Prize 2023: “Partial differential arise naturally as laws of nature, from the description of the flow of water to the growth of populations. These equations have been the constant subject of intense study since the days of Newton and Leibniz. However, despite substantial efforts by mathematicians over the centuries, fundamental questions related to stability or even uniqueness and the occurrence of singularities remain unresolved for some key equations. Throughout more than 40 years, Luis Caffarelli has made pioneering contributions to rule out or characterize singularities. This is known as regularity theory, and it captures key qualitative features of solutions, beyond the original functional analytic configuration.”
The above quote touches on two major themes. The first one is “differential equations,” which appear as a very powerful tool to describe the movement of bodies and the variation of geometric figures, as well as their states of equilibrium. These equations came to life as part of the differential calculus in the 17th century. They relate certain magnitudes (called system variables) with their relative rate of variation (i.e., with their derivatives). When the unknown variables depend on several space and/or time coordinates, the resulting equations are called “partial differential equations (PDEs).”
Over the last centuries the number of such equations with relevance in mathematics, physics, biology, and engineering has not stopped growing. Today the study of these equations is one of the most active branches of mathematics, and it is going through one of its golden periods due to the enormous influence of its results and techniques in diverse applications. Indeed, partial differential equations are used to mathematically describe processes that occur in nature and in so many fields of technology. The fundamental PDEs of physics describe phenomena arising in the study of waves and vibrations, the motion of fluids, the behavior of structures, electromagnetism, or the fundamentals of quantum mechanics. In topics closer to daily life, we find them in the study of the propagation of natural phenomena, such as fires or tsunamis, or the dynamics of invasive species, or the evolution of a disease in an organism or pandemic in a population. Let us also mention Euler’s equations for fluids, Maxwell’s for electromagnetism, Einstein’s for gravitation, Schrödinger’s and Dirac’s for quantum mechanics, or the Hamilton–Jacobi equations…, as major topics known to the public. Within mathematics itself, PDEs have deep connections with other fields such as the calculus of variations, differential geometry, harmonic analysis, probability theory, geometric measure theory, or computational mathematics.
Another important aspect of the equations studied by Caffarelli is “nonlinearity.” Let us examine this feature. Although nature has the good taste to resort to linear processes for many of its basic models, such as the transmission of waves or heat, and also the equations of quantum theory, it is well known that many of the most important processes in science are nonlinear, and understanding that added difficulty is part of the glory and the cross of the current mathematical profession.
Nonlinear PDEs are more difficult to solve than linear PDEs, and it may happen that they produce solutions that make no sense in the physical world. Hence, the work of deep analytical minds is needed to sort out the correct concepts and to show how to calculate with them. In the world of nonlinear problems, the superposition principle, which is a basic instrument in linear science, does not apply. Grosso modo, in a linear system the response corresponding to the sum of two data (whether input functions or external forces) is the sum of the two individual responses obtained separately with each of the data. This is the case, for example, in the world of Fourier analysis. However, in a nonlinear system, this is no longer true, and as a consequence the problem with general data cannot be reduced to the sum of solutions of certain basic blocks. Typical nonlinear analysis graphs are not flat surfaces or straight lines, but instead involve more arbitrary curves and surfaces.
Nonlinear equations appear in many natural phenomena, from the movement of fluids to phase transitions, from the shape of space-time to the behavior of stocks. These phenomena do not really obey the “principle of superposition of effects” and some of their “key features” (such as turbulence in fluids) are clearly the result of the “nonlinear” character of some underlying PDEs. These key features often show up as “oddities” where the equations that are used no longer hold in the usual way. Furthermore, there is no way to avoid the issue since such singularities are inherent to many problems. It is the mathematician’s task to understanding them and explaining to the scientist or engineer how to deal with them. Singularities are not a passing nuisance, on the contrary, they contain important, often crucial, information about the process where the model appears.
We may gladly declare that the mathematics of the late 20th century have been excellent in the study of those nonlinear processes that represent a stage of difficulty superior to the study of linear processes. Nonlinearity is an infinite source of complexity, and it is the origin of a many highly innovative theories. Chaos, shock waves, black holes, or climate evolution models are relevant scientific objects originated in the nonlinear worlds.
Caffarelli’s theorems have radically changed our understanding of a large class of nonlinear PDEs. The union of geometry and mathematical physics around the analysis of the equations produces pages of great beauty. We describe below the main mathematical contributions of Luis in more detail. The less expert reader may skip the details, at least on a first reading.
A. Regularity theory for free boundary problems
A central part of Caffarelli’s work concerns the regularity of the so-called free-boundary problems. These problems occur both in stationary processes and in processes that evolve with time. “Regularity” refers to the functions that appear as data or solutions, and it means in this context that such functions must have as many derivatives as they are required to ensure that they satisfy the equations in which they appear. The problem arises because we usually solve these and similar mathematical problems by resorting to approximate or numerical methods, after which the limit of such approximations is taken as the candidate to be a correct solution. The question is whether this limit is regular enough to satisfy the governing differential equation. This is an essential difficulty that Caffarelli tackles since his early papers, and to the study of which he contributed for many years. It is also remarkable that a lucky situation occurs: there are certain basic problems where the essential difficulties can be thoroughly examined and which have simple statements. It is true that in solving these “model problems” one encounters considerable technical difficulties, but this fact delights the researchers with a strong mathematical mind. Moreover, it was proved by additional research that solving the model problems opened the way for the mathematical study of realistic problems in different applications. Let us mention at this point that in this area there are multiple useful scientific and industrial applications.
We will present next some of these “model problems” where Caffarelli made fundamental contributions: the obstacle problem, the Stefan problem, the porous medium equation.
“Obstacle problem” (OP)
This is the model example for free boundaries of the stationary type.
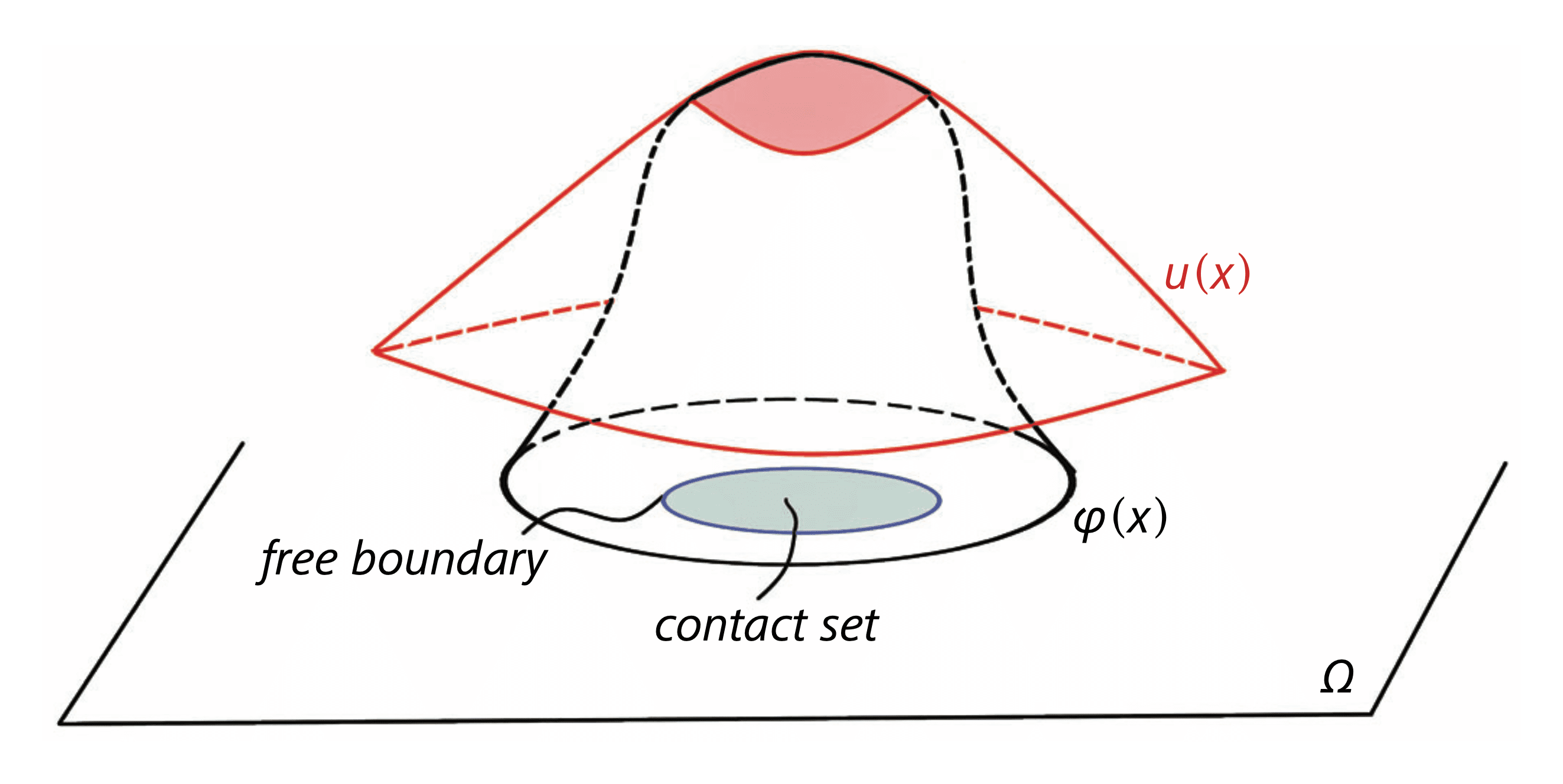
Suppose we are interested in determining the position of an elastic membrane that is subject to different forces, and that in addition certain conditions are imposed on the border that encloses it (technically called “the boundary”). According to the laws of elasticity, the equilibrium position of the membrane is described by an equation of state that in the simplest case reads
where represents the vertical position of the membrane over a point of a domain of the plane, represents the possible forces acting on the membrane, and is the Laplace operator. We are also given the function that represents the known height on the enclosing set where the membrane is attached to the border (the so-called “boundary conditions”). Then, it is well known in PDE theory that equation (E) together with the boundary conditions allow us to obtain a unique solution of the problem. Furthermore, if is a fairly regular function, then is also regular, even if the boundary conditions are not. These claims have been rigorously proven in the first half of the 20th century and were well known and studied years before.
The problem we have just described changes in difficulty when an “obstacle” is placed under the elastic membrane, . Then we have to consider the points inside the membrane (not on the boundary) where the membrane touches the obstacle. Obviously, the previous analysis does not apply. The modified analysis is best done if the domain is divided into two parts: a “contact set,” in which the membrane rests on the obstacle, and the remaining part in which the position of the membrane is located above the obstacle, the “non-contact set.” It then happens that in the latter region the elasticity equations must be satisfied, and it is proved that the equation of state (E) is valid there. In the best-case scenario, there is a clear line of separation between the two sets. It is called the free boundary, FB, so named because it is not known a priori, it must be calculated as part of solving the problem. Summing up, the whole problem becomes more complicated. It is about achieving two related goals, namely:
(1) Finding the set representing the part of the membrane that does not touch the obstacle.
(2) Solving the previous boundary problem (but now only in the domain where there is no contact) to find the position of the membrane. In the rest of the domain the membrane coincides with the obstacle.
This is the obstacle problem (OP). In short, the OP is a typical free boundary problem, FBP. Solving it requires combining the analysis of equations with differential geometry, two major areas of modern mathematics. Achieving such a combination is what constitutes the difficulty of the problem, which occupied the best minds in the field in the 1960s and 1970s. In 1977 Caffarelli surprised everyone with the seminal article in Acta Mathematica, where he considered the weak solutions of the OP (a class of possibly non-regular solutions obtained by functional methods, for example by minimizing the energy of the system), and then he proved that they are actually regular functions far away from the free boundary (provided the obstacle and the forces fulfill some minimal conditions).
Membrane over an obstacle. Notation instead of .
©All rights reserved.
And he also proved that this is true not only in two spatial dimensions, but also in all higher spatial dimensions. Furthermore, he showed that the free boundaries are indeed regular (hyper)surfaces, except for a possible “exceptional set” of singular points that are anyway very rare (technically, they form a set of small geometric measure).
The aforementioned singularities are not merely hypothetical; they do occur in practice. Thus, a duality is established: generic regularity versus exceptional singularity, a result that set the pace for further mathematical research on related topics ever since. The found regularity is technically called “Hölderian continuity,” and this has been the field of excellence of Luis Caffarelli. For details of the theory, see [5 L. A. Caffarelli, The obstacle problem revisited. J. Fourier Anal. Appl. 4, 383–402 (1998) ].
The result we have described uses quite novel methods that enabled Caffarelli in subsequent years to provide insightful solutions to a whole series of free boundary problems with applications to solid–liquid interfaces, jet and cavitation flows, and gas and liquid flows in porous media, as well as financial mathematics. Caffarelli’s regularity results are based on successively expanding the region close to the free boundary (a process called blow-up) and classifying the resulting extensions, where non-generic extensions correspond to the singularities of the free boundary. Exceptions to the regularity can occur, but they have a smaller dimension (as sets). The blow-up analysis is a very delicate technique that we will not explain further here.
“Stefan problem” (SP)
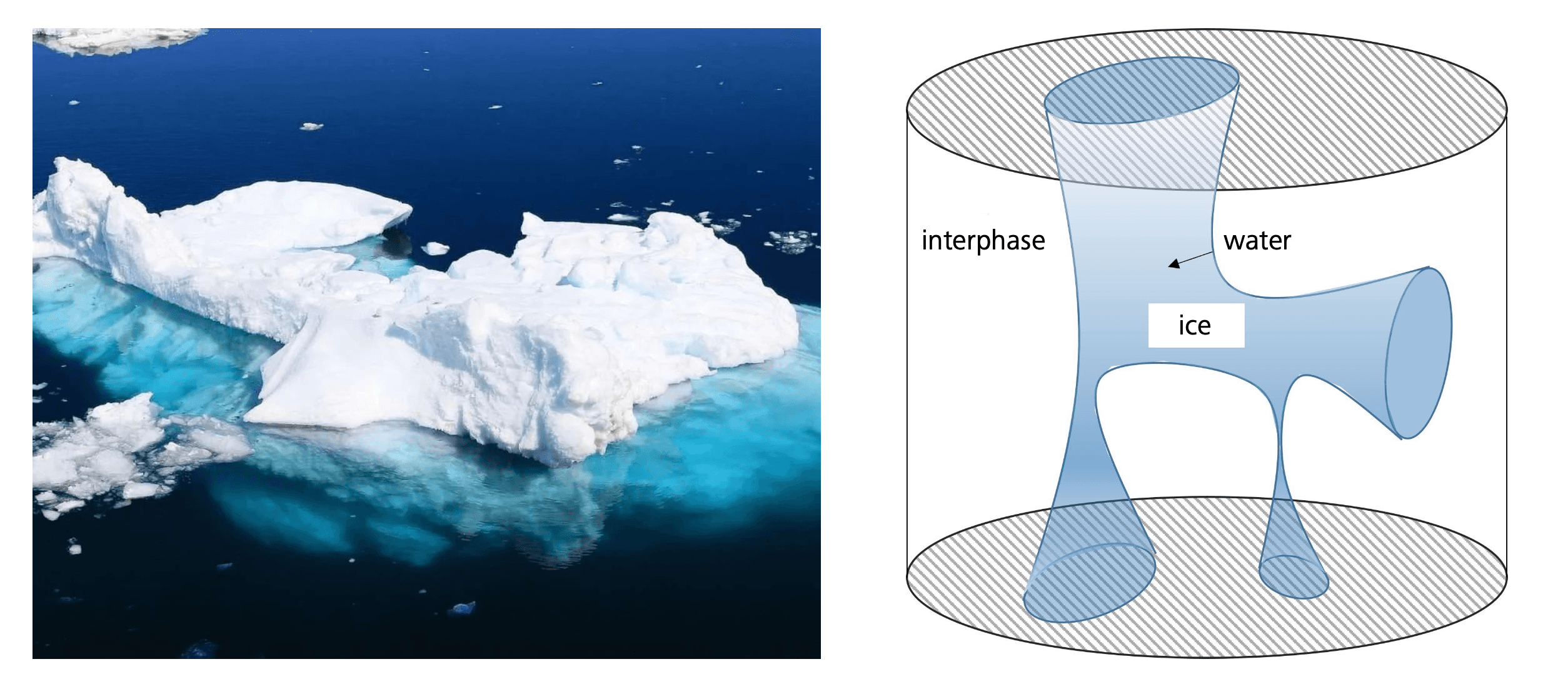
The most typical example of an evolution problem with a free boundary to be determined as part of the solution concerns the process of ice melting into water, called “Stefan problem” after the great mathematician-physicist Josef Stefan. This is a so-called phase transition problem. Here the free boundary is the interface between two phases of a medium, for example, water and ice. That interface is an unknown in the problem, that is, part of the whole solution that must be determined. Its location and properties are perhaps the most interesting features.
Water–ice system and its separation by a free boundary. The arrow in the right picture indicates free boundary motion from water to ice.
🅭🅯 CC BY 4.0As this interface moves over time, it can be more precisely called a “moving free boundary.” The SP is the standard problem in the mathematical description of phase transitions, with applications that include ecology, finance, and industry among many others.
There are many stationary and evolution free boundary problems in the theory of nonlinear PDEs that attracted Luis’s attention. We may just mention the problems of jet flows and cavities, the dam problem, or flows in porous media. This last problem allowed me to interact with him.
B. My scientific life and friendship with Luis, the porous medium equation
After meeting Luis Caffarelli and Don Aronson at a conference on free boundaries in Italy in the summer of 1981, I spent the academic year 1982/83 as a visitor in Minnesota, where Luis and Don were professors at the time, and we began to work on the regularity of the free boundary of the nonlinear version of the heat equation, now called PME, porous medium equation:
The equation with the exponent models the flow of water that permeates through a porous medium (Boussinesq, 1903). Here, denotes the height of the wet region over a flat impermeable bed. As usual, is the Laplace operator. In this problem, the interface between the wet and dry parts of the medium must be found along with the solution. The equation appears also (with different exponents ) in the study of the propagation of compressible gases in porous media following Darcy’s law (hence the popular name) and is applied in modeling oil reservoirs since the 1930s (Leibenzon and Muskat). There, the function stands for the gas density. Applications to plasma physics (in the Zeldovich school, 1950, Oleinik et al., 1958) and biology (population dynamics, Gurtin and McCamy, 1974) appeared later.3Information about these references and further applied literature can be found in [10 J. L. Vázquez, The porous medium equation: mathematical theory. Oxford Math. Monogr., Oxford University Press, Oxford (2007) ]. As part of the problem, in all of these applications there is a moving free boundary whose location is to be calculated (issue of specific application, say, engineering interest) and whose regularity as a surface is to be determined (topic of high interest in mathematics). Note that the existence of such a free boundary is implicit, i.e., it is not explicitly mentioned as part of the initial problem statement, it happens that it is present as part of the geometry of the solution. In any case, this problem is one of the motivations for a broad theory of degenerate diffusions in which Caffarelli was a dominant figure.
My collaboration with Luis became a lasting friendship. During all these decades I paid regular visits to him at his different locations: Chicago, Princeton, Courant, and Texas, as did many of his long-time collaborators, and the meetings included the many events that Luis (co)organized worldwide, motivated by his scientific leadership and generosity. These events had the added charm of his friendly character and down-to-earth approach.
Since the 1980s we worked on the regularity of free boundaries (1985, 1987), the heat propagation arising in combustion (1995), and the theory of viscosity solutions (1999). When, at the beginning of the new century, I was invited by Oxford University Press to write a book about the theory of the porous medium equation, which was by then well developed, I asked Luis to be coauthor and leader of the project. He replied by encouraging me to do it myself and offering me his help in any difficulties I could encounter, with an invitation to visit Texas when needed. The book [10 J. L. Vázquez, The porous medium equation: mathematical theory. Oxford Math. Monogr., Oxford University Press, Oxford (2007) ] took time to be written and appeared in 2007. This is maybe a good place to express once more my gratitude and recall the many pages of the book that contain the master’s ideas.
Life went on. In the same year, 2007, Luis invited me to embark on the study of non-local parabolic equations, his passion at the time, as we will see below. Non-local parabolic equations and fractional Laplacian operators have occupied much of my time, and the time of my students and collaborators, ever since. But that is recent history, let us return to the older times and visit other provinces where Luis soon showed his best mathematics.
C. The regularity of viscous fluids, the Navier–Stokes equations
In 2014 the American Mathematical Society (AMS) awarded the Leroy P. Steele Prize, one of the highest honors in mathematics, to Luis Caffarelli along with Robert Kohn and Louis Nirenberg. It did so for his “seminal contribution to research,” being honored for his aforementioned 1982 article [1 L. Caffarelli, R. Kohn and L. Nirenberg, Partial regularity of suitable weak solutions of the Navier–Stokes equations. Comm. Pure Appl. Math. 35, 771–831 (1982) ] on the regularity or possible singularity of solutions to the Navier–Stokes equations which govern the motion of viscous fluids. The mention says: “This paper was and remains a milestone in the understanding of the behavior of solutions to the Navier–Stokes equations and has been a source of inspiration for a generation of mathematicians.” The Navier–Stokes equations are fundamental to the mathematical understanding of fluid dynamics and the existence and smoothness of solutions is one of the seven Clay Mathematics Institute’s Millennium Prize Problems.
The Caffarelli–Kohn–Nirenberg result deals with partial regularity, something already found in the study of free boundaries, but now in a very different, seemingly unrelated topic: it states that there is still the possibility of singularities appearing in the density of the flow after some time, but in any case the set of singular points in space-time is very small, not very dense (technically, it has a very small geometric measure). In particular, it cannot contain any curve pieces. The possible singular Navier–Stokes turbulence would therefore be quite an exceptional event, if it occurs. The result represented a great advance in our understanding of these equations and has motivated many subsequent developments and simplifications. But the advances made from 1982 till today do not have at all the depth and scope of the CKN result. The problem of total regularity is still open.
D. Fully nonlinear problems, Monge–Ampère equation, optimal transportation
Caffarelli’s regularity theorems from the 1990s represented a major advance in our understanding in a third direction, again very different from the previous ones. This concerns the Monge–Ampère equation, a highly nonlinear partial differential equation that is used, for example, to construct surfaces of a prescribed Gaussian curvature. The great Russian mathematician Pavel S. Alexandrov obtained important existence results in this direction. Caffarelli, in collaboration with Louis Nirenberg and Joel Spruck, established essential properties of the solutions, with notable additional contributions from Lawrence C. Evans and Nicolai V. Krylov. Caffarelli later closed the gap in our understanding of singularities by showing that certain explicitly known examples of singular solutions are the only possible ones.
Starting from the Monge–Ampère equation, Caffarelli devoted several works to the study of the class of equations called completely nonlinear. His book, written in collaboration with Xavier Cabré, Fully Nonlinear Elliptic Equations [6 L. A. Caffarelli and X. Cabré, Fully nonlinear elliptic equations. Amer. Math. Soc. Colloq. Publ. 43, American Mathematical Society, Providence, RI (1995) ], is a mandatory reference on this topic.
Caffarelli, together with his collaborators, has applied these results to the Monge–Kantorovich “optimal mass transportation” problem, building on earlier work by Yann Brenier. His knowledge of the Monge–Ampère equations enabled him to make fundamental contributions in this area as well.
Example of a turbulent fluid.
©C. Fukushima and J. Westerweel
E. Integro-differential operators, anomalous diffusion, and non-local processes
Since the beginning of this century, there has been an enormous interest in research that deals with the interactions between particles or populations, or in the world of information. Recently, this interest has focused on considering actions at a distance, where notable effects are felt far away from the origin of the signal. In particular, these interactions do not follow the well-known Brownian-type decay patterns. The canonical form of these interactions is what is known as Lévy processes in probability and as “fractional Laplacian operators” in mathematical analysis and PDEs. The growth of this theory within PDEs has been spectacular in the last two decades. A fundamental reference in the mathematical analysis of this area is the 1970 article by Luis Caffarelli and Luis Silvestre: An extension problem related to the fractional Laplacian [3 L. Caffarelli and L. Silvestre, An extension problem related to the fractional Laplacian. Comm. Partial Differential Equations 32, 1245–1260 (2007) ]. It heralded a new era in the research on such diffusive phenomena, and it has become a standard reference for scholars in the area.
The applications of fractional calculus are today varied and numerous. To name a few, we mention quasi-geostrophic flows, turbulence, molecular dynamics, stellar relativistic quantum mechanics, as well as various applications in probability and finance.
In a paradigmatic example, Luis Caffarelli and Alexis Vasseur obtained deep regularity results for the quasi-geostrophic equation, a popular model with application to fluid theory. In their 2010 article, Drift diffusion equations with fractional diffusion and the quasi-geostrophicequation [7 L. A. Caffarelli and A. Vasseur, Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. of Math. (2) 171, 1903–1930 (2010) ], Caffarelli and Vasseur demonstrate the total absence of singularities in this model. This result is somewhat related to the possible existence of singularities in the Navier–Stokes problem. Contrary to the current guess about the existence of singularities for the NS problem, here the mathematical analysis is able to eliminate them. May this shed some light on NS?
In another direction, the classical idea of minimal surface, and that of perimeter of a solid have been successfully extended to the context of long-range interactions by Luis Caffarelli and his collaborators, such as Jean-Michel Roquejoffre, Ovidiu Savin and Enrico Valdinoci. These lines of research are supposed to have a great future and reflect the deep interaction of geometry and physics in Caffarelli’s mind, with the theory of probability close by.
Finally, the combination of nonlinear diffusion ideas with non-local interactions has given rise to the theories of “nonlinear and non-local diffusion” that have been developed in recent years, particularly in projects of Luis with Spanish collaborators, in a series of influential applications, that are being used in the mathematical modeling of processes in various fields of science. An example of this vitality is, for example, the new book on the subject: Integro-Differential Elliptic Equations, by Xavier Fernández-Real and Xavier Ros-Oton [8 X. Fernández-Real and X. Ros-Oton, Integro-differential elliptic equations. Progr. Math. 350, Birkhäuser, Cham (2024) ].
In addition, Caffarelli has made outstanding contributions to homogenization theory, which seeks to characterize the effective or macroscopic behavior of media that have a microstructure, for example, are made of a composite material. A typical problem in this theory concerns a porous medium, such as a hydrocarbon reservoir, where one has a solid rock with pores. The system has a complex and largely unknown structure, through which fluids flow. Nonlinear mathematics has done important inroads in that field.
Final notes
Caffarelli is an exceptionally prolific mathematician: he has written more than 320 mathematical articles in the best journals with more than 130 collaborators, ranging from some of the most distinguished mathematicians to very bright young people from all over the world. He has had more than 30 doctoral students over a period of almost 5 decades and has more than 160 descendants4161, according to the Mathematics Genealogy Project.. Luis has always been a very open scientist and a dedicated organizer, who keenly thought about reaching out to bright students everywhere. He has a huge number of friends in the PDE community, and he had a very strong influence on the work of many brilliant scientists. The list of names goes from the old generation—let me just mention Don Aronson, Avner Friedman, and Louis Nirenberg—to the younger generation, which may be exemplified by Alessio Figalli, Fields Medalist 2018, who stayed many years in Austin and added brilliant pages to Luis’s heritage.
Luis Caffarelli was never very fond of writing monographs, and that is a real pity. However, two long books reflect two areas of his teaching. One of them is the already mentioned book with Xavier Cabré [6 L. A. Caffarelli and X. Cabré, Fully nonlinear elliptic equations. Amer. Math. Soc. Colloq. Publ. 43, American Mathematical Society, Providence, RI (1995) ], dating from his years at Courant, and the other is the book with his long-time collaborator Sandro Salsa [2 L. Caffarelli and S. Salsa, A geometric approach to free boundary problems. Grad. Stud. Math. 68, American Mathematical Society, Providence, RI (2005) ] with a very suitable title: A Geometric Approach to Free Boundary Problems.
Luis has had and continues to have an enormous impact on the field. In his speech in Oslo last May, Jan Philip Solovej, president of the European Mathematical Society (EMS), recalled the impression made on him as a young man when reading some of Luis’s articles: “There was this beautiful idea of controlling or taming the scary difficulties by intuitive geometric ideas of shapes. Taming difficulties is what mathematics is often about, and Professor Caffarelli has, more than anyone else, mastered the art of taming irregularities.”
Luis Caffarelli has had a huge influence on the development of partial differential equations in several countries, mainly the US, Argentina, Spain, Italy, Greece, Korea, and China (to keep the list short). His collaboration with Spanish authors dates back to the 1980s and 1990s, after we met in Italy. He collaborated with many Spanish researchers, like Xavier Cabré, Antonio Córdoba, Ireneo Peral, Rafael de la Llave, Fernando Soria, and several younger ones. Luis has participated in numerous courses and schools in Spain, most notably in the series of UIMP Santander Summer Courses that we organized in the wonderful setting of the Magdalena Palace in Santander, thanks to his support and presence. Luis was named doctor honoris causa by the Autonomous University of Madrid in 1992. Since 2015, he has been a foreign academician of the Spanish Royal Academy of Sciences in recognition of his fruitful involvement with Spanish mathematicians for so many years. Luis received the Honorary Fellowship from RSME, the Royal Spanish Mathematical Society, and then the Rey Pastor Award (2017), on similar grounds.
Along with all of the above, we must mention his proverbial hospitality and the well-deserved reputation of being a great cook, in the Argentine-Italian tradition. Many of us remember memorable dinners with Luis and his wife Irene Gamba, also a mathematician, in their house in Austin.
Acknowledgements. The author is grateful to a number of friends and colleagues of Luis Caffarelli, who have contributed to improve this text with suggestions and corrections. He is especially grateful to Victoria Otero who coauthored an article with him to appear in Spanish, [9 V. Otero and J. L. Vázquez, Luis Caffarelli, Premio Abel de las matemáticas 2023. Revista de la Fundación Ramón Areces, to appear ], where, along with many of the above ideas, they talk about his influence in Spain.
- 1
Notices of the AMS: https://www.ams.org/notices/201404/rnoti-p393.pdf. See also: https://www.ams.org/journals/notices/201808/rnoti-p1019.pdf
- 2
Quoted from the article in New Scientist, “Mathematician wins Abel Prize for solving equations with geometry,” 22 March 2023, by Alex Wilkins.
- 3
Information about these references and further applied literature can be found in [10 J. L. Vázquez, The porous medium equation: mathematical theory. Oxford Math. Monogr., Oxford University Press, Oxford (2007) ].
- 4
161, according to the Mathematics Genealogy Project.
References
- L. Caffarelli, R. Kohn and L. Nirenberg, Partial regularity of suitable weak solutions of the Navier–Stokes equations. Comm. Pure Appl. Math. 35, 771–831 (1982)
- L. Caffarelli and S. Salsa, A geometric approach to free boundary problems. Grad. Stud. Math. 68, American Mathematical Society, Providence, RI (2005)
- L. Caffarelli and L. Silvestre, An extension problem related to the fractional Laplacian. Comm. Partial Differential Equations 32, 1245–1260 (2007)
- L. A. Caffarelli, The regularity of free boundaries in higher dimensions. Acta Math. 139, 155–184 (1977)
- L. A. Caffarelli, The obstacle problem revisited. J. Fourier Anal. Appl. 4, 383–402 (1998)
- L. A. Caffarelli and X. Cabré, Fully nonlinear elliptic equations. Amer. Math. Soc. Colloq. Publ. 43, American Mathematical Society, Providence, RI (1995)
- L. A. Caffarelli and A. Vasseur, Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. of Math. (2) 171, 1903–1930 (2010)
- X. Fernández-Real and X. Ros-Oton, Integro-differential elliptic equations. Progr. Math. 350, Birkhäuser, Cham (2024)
- V. Otero and J. L. Vázquez, Luis Caffarelli, Premio Abel de las matemáticas 2023. Revista de la Fundación Ramón Areces, to appear
- J. L. Vázquez, The porous medium equation: mathematical theory. Oxford Math. Monogr., Oxford University Press, Oxford (2007)
Cite this article
Juan Luis Vázquez, Luis Caffarelli, winner of the Abel Prize 2023. Eur. Math. Soc. Mag. 132 (2024), pp. 14–22
DOI 10.4171/MAG/192