Are old mathematicians useless?

In the interest of better readability, this article is divided into four sections: ⁠(1)⁠Hardy’s standpoint on the matter, ⁠(2)⁠ examples of useful old mathematicians, ⁠(3)⁠ the author’s standpoint, and ⁠(4)⁠final remarks.

1 Hardy’s standpoint

We begin with some comments about Godfrey Harold Hardy, who lived from 7 February 1877 until 1 December 1947. Hardy urgently requests that old mathematicians should stop mathematical research, but he never says what they could do for the rest of their lives.

The subsequent quotations can be found in [⁠5⁠ G. H. Hardy, A mathematician’s apology. (With a foreword by C. P. Snow.) Canto, Cambridge University Press, Cambridge (1992) , pp. 72 and 148].

I do not know an instance of a major mathematical advance initiated by a man past fifty. A mathematician may still be competent enough at sixty, but it is useless to expect him to have original ideas.

In the preceding statements Hardy uses two bounds, “fifty” and “sixty”. In my opinion, this difference is inessential, since any age limit should be avoided.

Hardy wrote his “Apology” at the age of 63. We know from C. P. Snow’s foreword that, fully aware of his decreasing mental power, Hardy was already extremely depressed. In the summer of 1947 he even tried to commit suicide; see [⁠5⁠ G. H. Hardy, A mathematician’s apology. (With a foreword by C. P. Snow.) Canto, Cambridge University Press, Cambridge (1992) , p. 54]. When following Hardy’s life strategy, his true fans should take these facts into account.

Mathematicians certainly attain the maximum of their efforts at an age much less than fifty, which is also reflected by the Fields Medal. In Hardy’s words: “Mathematics is a young man’s game”; see [⁠5⁠ G. H. Hardy, A mathematician’s apology. (With a foreword by C. P. Snow.) Canto, Cambridge University Press, Cambridge (1992) , p. 70]. But some are able to keep their high level very long. More cannot be expected.

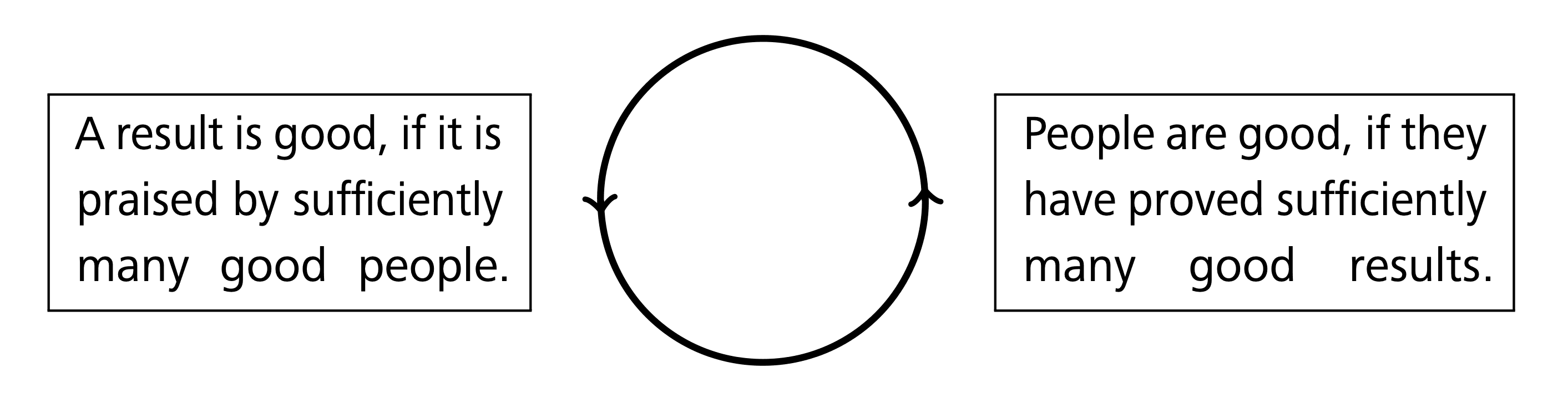
Hardy made several clever comments concerning the definition of “good” mathematics, which should be read in the original; see [⁠5⁠ G. H. Hardy, A mathematician’s apology. (With a foreword by C. P. Snow.) Canto, Cambridge University Press, Cambridge (1992) , p. 89]. However, in real life one falls the circulus vitiosus shown in Figure ⁠1⁠.

2 Useful old mathematicians

The selection of successful old mathematicians is rather problematic. If we assume that there are at least five candidates in each of the 63 areas in the MSC2020 Mathematics Subject Classification System, then our task is to chose, by some kind of lottery, a few candidates out of more than 300. For sure, there is no shortage of examples. On the contrary, we have too many. Hopefully, the following (very subjective) choice is acceptable.

To keep this article short and effective, I only name specific persons, who proved remarkable results “past fifty”; details are not discussed.

Of course, we have the absolute giants: L. Euler (1707–1783), J. Liouville (1809–1882), K. Weierstrass (1815–1897), and A. Einstein (1879–1955).

What follows is a random list of further candidates to which everybody could add his own favourites: P. Erdős (1913–1996), I. Gelfand (1913–2009), E. Hlawka (1916–2009), B. Mandelbrot (1924–2010), J. P. Kahane (1926–2017), I. Gohberg (1928–2009), Sir M. F. Atiyah (1929–2019), D. Edmunds (1931), A. Schinzel (1937–2021), R. Schneider (1940).

Women are represented by O. Taussky-Todd (1906–1995) and D. Maharam (1917–2014).

To evaluate the late work of these personalities would be arrogant; what remains is my greatest respect.

Already older than sixty, Erdős (800), Gohberg (286), Gelfand (195), Edmunds (172), Kahane (142), Schinzel (137), Atiyah (121), Triebel (98), Mandelbrot (87), Schneider (85), Hlawka (84), Taussky (71), Johnson (39), Maharam (23), etc. wrote many publications. The parentheses above enclose quite exact numbers, found by using MR. Certainly, it is not only a speculation to expect that these contributions contain a lot of top results.

The subsequent table presents the reasonable number of ten examples in which a “performance peak” is attained after fifty; collected by using MR, zbMATH, www, and the references.

L. Vietoris (1891–2002) delivered his last paper [⁠15⁠ L. Vietoris, Über das Vorzeichen gewisser trigonometrischer Summen. III. Österreich. Akad. Wiss. Math.-Natur. Kl. Sitzungsber. II 203, 57-61 (1994) ] at the age of 103; MR confirms the substantial number of twelve citations.

3 The author’s standpoint

My own lifework provides some supplementary information on the issues discussed so far.

What follows is a short autobiography. Hopefully, the reader will get a positive picture of the author. This would justify all the efforts spent to write this article.

Indeed, Hardy’s “A Mathematician’s Apology” has become the main source of my mathematical philosophy. I learnt a lot from him. There is only one critical point: My strong rejection of the proposed mathematical suicide.

Without any intention to compare myself with Hardy, I vehemently state that loving mathematics knows no age limits.

Hardy stressed that intellectual curiosity, ambition, professional pride, and the desire for reputation are the driving forces behind the best works of the world; see [⁠5⁠ G. H. Hardy, A mathematician’s apology. (With a foreword by C. P. Snow.) Canto, Cambridge University Press, Cambridge (1992) , pp. 78–80]. He did not mention pleasure, and even love. Mathematical research should be considered not only as a competition, but also as a hobby. Of course, I am very pleased if somebody likes my results. However, I also appreciate the achievements of others. We are all in the same boat.

Here is a list of mathematical objects that have been of interest for me; half of them were introduced by myself and are often in use (by specialists).

• 1960 $\Phi$-operators

• 1962 perfect spaces of vector-valued sequences

• 1962 nuclear locally convex spaces

• 1963 related operators

• 1963 approximation numbers

• 1967 absolutely $p$-summing operators

• 1968 operator ideals

• 1972 $s$-numbers

• 1972 limit orders and their diagrams

• 1980 Weyl numbers

• 1980 eigenvalue distributions

• 1981 approximation spaces

• 1981 classical traces

• 1991 singular traces

• 1994 ideal norms associated with orthonormal systems

• 2012 shift-monotone sequence ideals

• 2012 Pietsch correspondence

• 2023 Lorentz sequence ideals

All research I did is concentrated on these concepts and their interplay. My interest in history started at the age of fifty.

From 1992 to 2000 I was twice elected as an Expert for Mathematics of the German Research Foundation. During the second period, I even became the chairman of the Mathematics Committee and wrote about 400 final reports.

I have published seven books; one is co-authored with my pupil Jörg Wenzel. “Nukleare lokalkonvexe Räume” has been translated from German into Russian and English, “Operator Ideals” from English into Russian. Important are also “Theorie der Operatorenideale” (1972), in German, a research program, and the “History of Banach Spaces and Linear Operators” (2007).

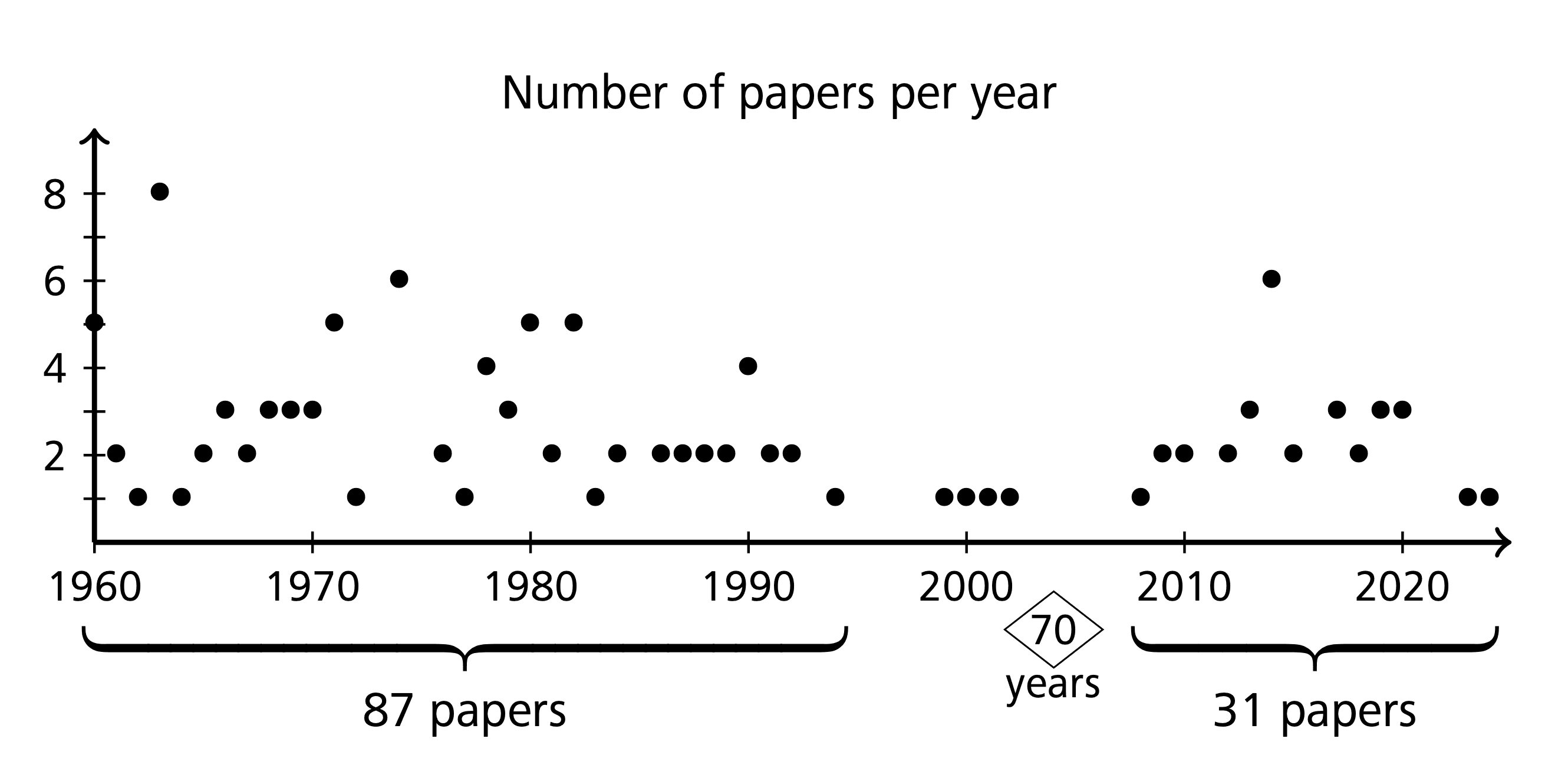
Figure ⁠2⁠ illustrates the time distribution of my 122 papers. Note that the irregularity in the period from 1996 to 2007 is caused by my work for the German Research Foundation and by writing the “History” book.

Following Hardy’s mantra, I should have finished in 2007 with my comprehensive historical book. However, I started a “second” mathematical life, in which the basic approach to the theory of traces was fully rebuilt and essentially simplified; see [⁠8⁠ S. Lord, F. Sukochev and D. Zanin, Singular traces. Vol. 1: Theory. De Gruyter Stud. Math. 46/1, De Gruyter, Berlin (2021) , Chapter 4] and my paper [⁠9⁠ A. Pietsch, A new approach to operator ideals on Hilbert space and their traces. Integral Equations Operator Theory 89, 595–606 (2017) , submitted at the age of 82]. The paper on Lorentz sequence spaces also provides new insights; see [⁠10⁠ A. Pietsch, Lorentz spaces depending on more than two parameters. Ann. Funct. Anal. 15, article no. 16 (2024) , submitted at the age of 89].

Please, consider myself just as a supplementary example.

4 Final remarks

Old colleagues may have lost their mental power or enthusiasm to continue mathematical research. So each person should alone decide what is possible and desirable. We need to respect the specific personalities. Tolerance is the main point.

Of course, proving theorems gives great satisfaction to old mathematicians. However, in my opinion, seniors also have the duty to pass on their know-how to the younger generations. They should communicate ideas about future developments; presenting collections of open problems is a good example.

Knowing the standpoints of many people is extremely important; but what really counts is the personal reaction of each individual reader. My final wish: Pay attention to your old colleagues and appreciate their lifework.

Albrecht Pietsch was born in 1934 in Zittau (Saxony), and studied at the University of Leipzig from 1953 to 1958. He received the Dr. rer. nat. from Dresden University of Technology in 1959 and the Dr. rer. nat. habil. from Humboldt University Berlin in 1963. Starting in 1965, Pietsch was a professor of analysis at the University of Jena for 35 years, where he supervised 27 Ph.D. students. Besides his monographs Nuclear locally convex spaces, Operator ideals, Eigenvalues and s-numbers, Orthonormal systems and Banach space geometry (co-author: J. Wenzel) and History of Banach spaces and linear operators, he published more than 120 research papers. From 1971 to 1990, National-Prize-Holder Pietsch was a member of the Academy of Sciences of the German Democratic Republic, and since 1974 he is a member of the Leopoldina (now German National Academy of Sciences). Honorary doctorates were awarded to him by the universities of Paderborn (1998) and Pretoria (2008). Present status: Ostdeutscher Rentner. a.pietsch@uni-jena.de

References

1. S. A. Argyros and R. G. Haydon, A hereditarily indecomposable ℒ∞-space that solves the scalar-plus-compact problem. Acta Math. 206, 1–54 (2011)
2. E. Calabi and J. G. Cao, Simple closed geodesics on convex surfaces. J. Differential Geom. 36, 517–549 (1992)
3. H. Cartan, Théories cohomologiques. Invent. Math. 35, 261–271 (1976)
4. T. Figiel, W. B. Johnson and A. Pełczyński, Some approximation properties of Banach spaces and Banach lattices. Israel J. Math. 183, 199–231 (2011)
5. G. H. Hardy, A mathematician’s apology. (With a foreword by C. P. Snow.) Canto, Cambridge University Press, Cambridge (1992)
6. N. Kalton and F. Sukochev, Rearrangement-invariant functionals with applications to traces on symmetrically normed ideals. Canad. Math. Bull. 51, 67–80 (2008)
7. N. J. Kalton and F. A. Sukochev, Symmetric norms and spaces of operators. J. Reine Angew. Math. 621, 81–121 (2008)
8. S. Lord, F. Sukochev and D. Zanin, Singular traces. Vol. 1: Theory. De Gruyter Stud. Math. 46/1, De Gruyter, Berlin (2021)
9. A. Pietsch, A new approach to operator ideals on Hilbert space and their traces. Integral Equations Operator Theory 89, 595–606 (2017)
10. A. Pietsch, Lorentz spaces depending on more than two parameters. Ann. Funct. Anal. 15, article no. 16 (2024)
11. H. Poincaré, Sur un théorème en géométrie. Rend. Circ. Mat. Palermo 33, 375–407 (1912)
12. T. Royen, A simple proof of the Gaussian correlation conjecture extended to some multivariate gamma distributions. Far East J. Theor. Stat. 48, 139–145 (2014)
13. L. Schwartz, Radon measures on arbitrary topological spaces and cylindrical measures. Tata Institute of Fundamental Research Studies in Mathematics, No. 6, Oxford University Press, London (1973)
14. H. Triebel, Hybrid function spaces, heat and Navier–Stokes equations. EMS Tracts Math. 24, European Mathematical Society (EMS), Zürich (2014)
15. L. Vietoris, Über das Vorzeichen gewisser trigonometrischer Summen. III. Österreich. Akad. Wiss. Math.-Natur. Kl. Sitzungsber. II 203, 57-61 (1994)
16. Y. Zhang, Bounded gaps between primes. Ann. of Math. (2) 179, 1121–1174 (2014)