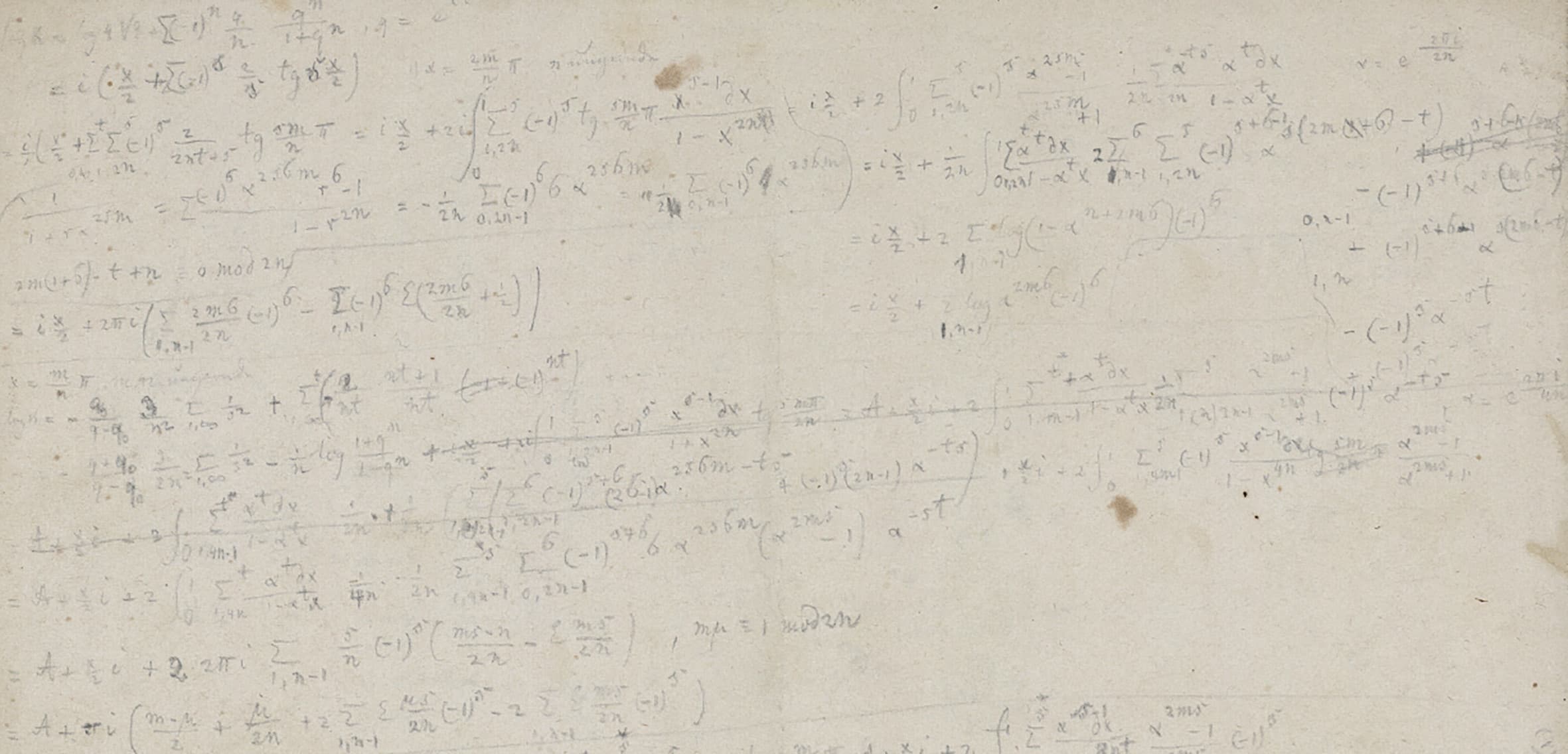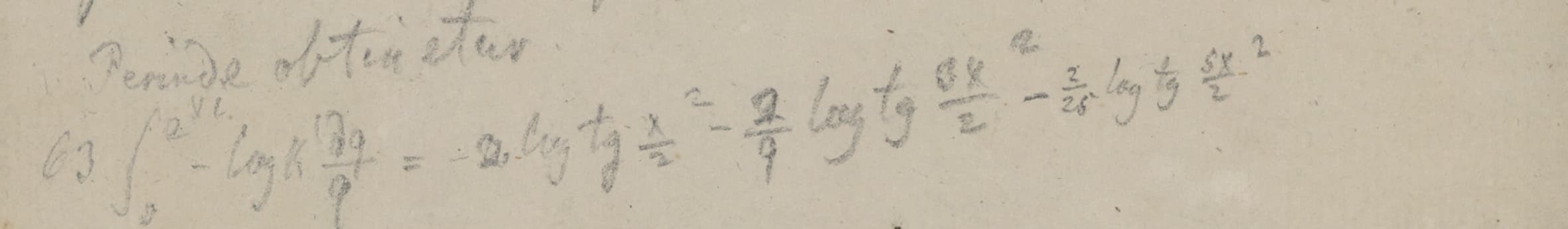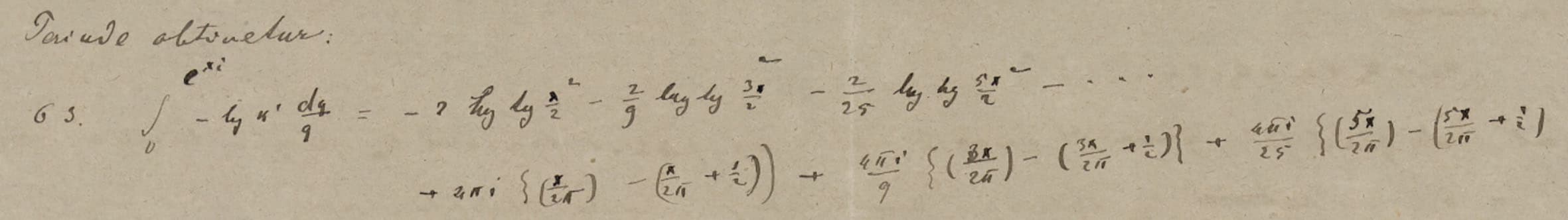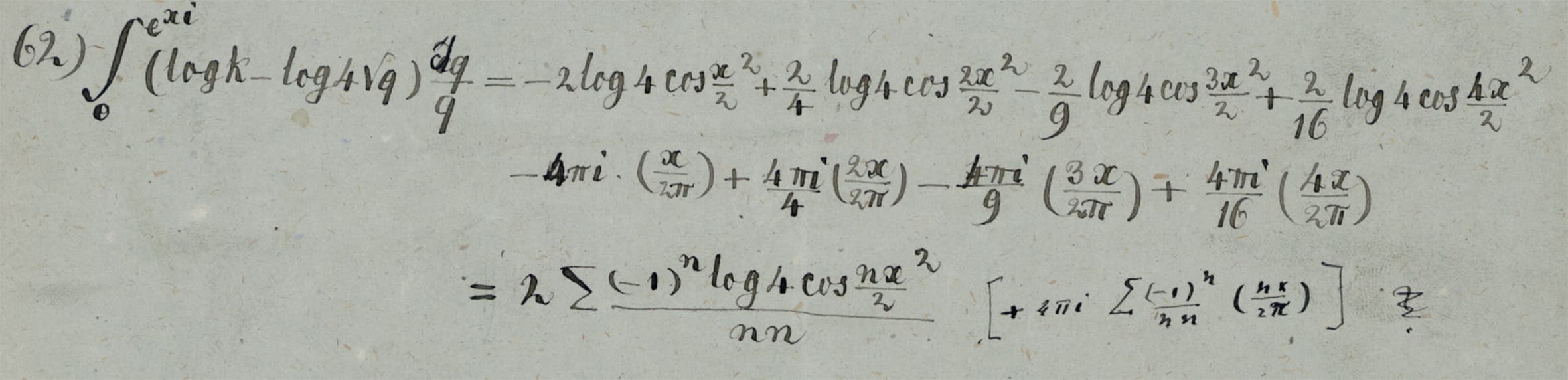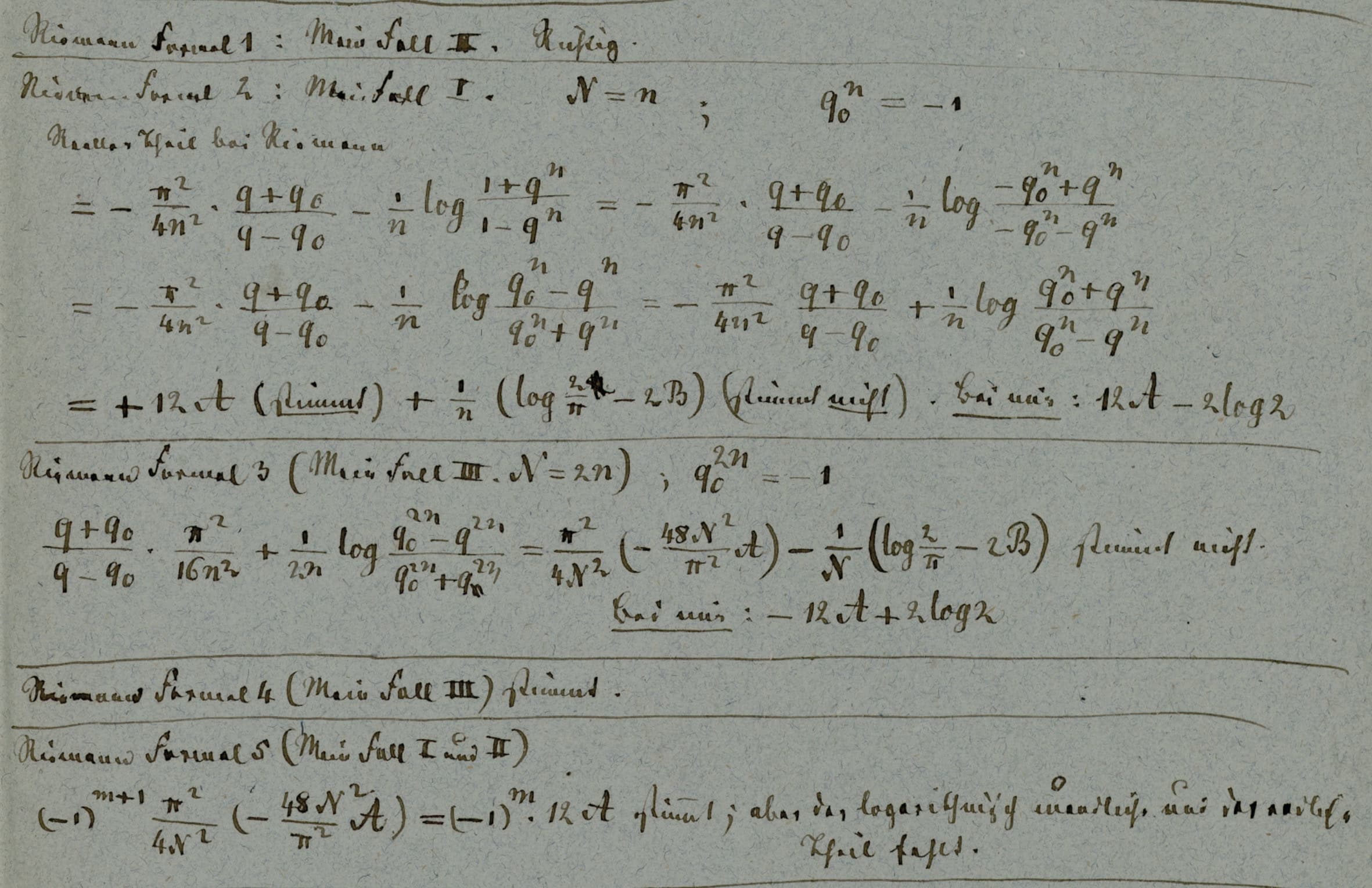A complex history and a wealth of archive
In 1876 were published Bernhard Riemann’s (1826–1866) Gesammelte mathematische Werke und wissenschaftlicher Nachlass (Collected mathematical works and scientific archive). These collected works were edited by Heinrich Weber (1842–1913) and Richard Dedekind (1831–1916) and published by B. G. Teubner.1At this time, a considerable number of projects of publishing collected works were launched in France, Germany, Italy, the United Kingdom … The publisher B. G. Teubner, created in 1811 in Leipzig, which specialised in scientific editions (broadly construed, i.e., philology, history, mathematics, physics, etc.), was one of the leading publishers for this type of book in Germany. – Steven W. Rockey from Cornell University published a very complete list of collected works in mathematics: mathematics.library.cornell.edu/about-collected-works/.
Riemann and Dedekind met while they were Gauss’ students in Göttingen. They defended their doctoral dissertation within a year of each other (Riemann in 1851 and Dedekind in 1852), and their respective Habilitation with only a few days difference in 1854. Following this, they both worked as Privatdozenten in Göttingen, during which time Dedekind followed Riemann’s classes. In 1858 Dedekind was offered a position in Zürich and Riemann a post in Göttingen, and they remained friends until Riemann’s untimely death in 1866.
It was Riemann’s wish that Dedekind would be the editor of his collected works and in charge of his scientific archive after his death. Struggling with this difficult editorial enterprise, in early 1872, Dedekind accepted to work with Alfred Clebsch (1833–1872), who had taken Riemann’s chair in Göttingen. Seven of the most complete of Riemann’s unpublished works were first published posthumously in various mathematical journals.2[22 B. Riemann, Ueber die Fläche vom kleinsten Inhalt bei gegebener Begrenzung. In [25], 1st ed. (1876) 283–315, 2nd ed. (1892), 301–335; transl. En., 387–322. First published in 1867 ] was edited by Karl Hattendorff (1834–1882), [21 B. Riemann, Mechanik des Ohres. In [25], 1st ed. (1876), 316–330; 2nd ed. (1892), 338–352. First published in 1867 ] by Ernst Schering (1824–1889) and Friedrich Henle (1809–1885), the other texts presumably by Dedekind. – A note on the dates of the publications: when it is possible to date Riemann’s texts, these are the given dates; when it is not, the dates are that of the first publication. Clebsch did not wish to publish more of Riemann’s manuscripts as he felt the edition, as he wanted it to be, was nearing completion (according to his letters to Dedekind, published in [8 P. Dugac, Richard Dedekind et les fondements des mathématiques. Vrin, Paris (1976) ], and to Dedekind’s first letter to Weber in [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) ]). Clebsch’s sudden death in 1872 put the edition in some difficulty. Dedekind’s teaching duties kept him from handling the project by himself. Eventually, upon meeting Heinrich Weber in Zürich in 1873,3Maybe a less famous name than Riemann, Clebsch and Dedekind, Heinrich Weber was a prominent mathematician throughout his career. He studied in Heidelberg, Leipzig and Königsberg. He taught in Heidelberg, Zürich, Königsberg (where he taught number theory to Hilbert and Minkowski), Berlin, Marburg, Göttingen, and Strasbourg. He worked extensively on complex function theory, number theory, and algebra. Among several important contributions to the latter, his Lehrbuch der Algebra was to be the main reference for teaching algebra in the German speaking world until the publication of Van der Waerden’s Moderne Algebra in 1930. He also made contributions to mathematical physics, and published Die partiellen Differentialgleichungen der mathematischen Physik nach Riemann’s Vorlesungen, which was, for a long time, the only reference for Riemann’s mathematical physics. Weber was also actively involved in the mathematical community, for example he was a member of the editorial committee of the Mathematische Annalen and a founding member of the Deutsche Mathematiker-Vereinigung. Dedekind offered him the responsibility of the edition, which he accepted. At this stage, Dedekind wished to retreat from the project, but eventually became more involved in the edition of some of the manuscripts. Both Weber and Dedekind wished to publish more of Riemann’s unpublished archive, and it took them two additional years to complete the edition, during which time they also had help from Hermann Schwarz (1843–1921) in working on [20 B. Riemann, Sullo svolgimento del quoziente di duo serie ipergeometricho in frazione continua infinita. In [25], 1st ed. (1876), 400–406; 2nd ed. (1892); transl. En., 409–416. First published in 1863 ].
The final product of this ten-year editorial endeavour, Riemann’s Gesammelte mathematische Werke und wissenschaftlicher Nachlass, is one volume divided into three parts and two appendices: the first part contains the 11 papers published by Riemann in his lifetime; the second part contains the 7 papers published posthumously in journals as mentioned above; and the third part contains 12 unpublished texts from Riemann’s archive. The two appendices are a selection of Riemann’s philosophical writings, and a biography written by Dedekind on the basis of letters from Riemann’s widow, Elise Riemann.
Riemann’s collected works were republished in 1892, by Weber. In the preface, he explained that Riemann’s texts were still very relevant in 1892. Two important changes in the edition should be mentioned. Firstly, the text Verbreitung der Wärme im Ellipsoid (Diffusion of heat in an ellipsoid) [28 B. Riemann, Verbreitung der Wärme im Ellipsoid. In [25], 2nd ed. (1892), 437–439; transl. En., 425–428. First published in 1892 ], which was briefly discussed and eventually excluded from the 1876 edition, was published. There are no indications or correspondence that indicate why it was initially excluded (in fact, the letters suggest that it was going to be published in 1876), nor why it was finally published in 1892. Secondly, the notes and commentaries by the editors were revised (following feedback on the first edition) and completed. In 1876, 4 texts were commented (30 pages of commentaries), while in 1892, 10 texts were commented (for a total of 60 pages of commentaries). A third edition was published in 1902 by Max Noether and Wilhelm Wirtinger. The sole but very notable change here is the addition of over a hundred pages of notes from Riemann’s lectures (on Abelian, elliptic, hyperelliptic functions, hypergeometric series, etc.) which had only recently become known.4In 1990, the 1902 edition was reprinted along with additions. A French translation appeared in 1898, translated by Léonce Laugel and published by Gauthiers-Villars (see p. Shaping the book and shaping the image of the editee). The first English translation appeared in 2004 [29 B. Riemann, Collected Papers. Kendrick Press, Heber City (2004) ].
Only for the 1876 edition do we have, rather exceptionally, extensive documentation on the process of editing Riemann’s collected works. This is one reason why my focus in this paper will be this first edition.5Unless stated otherwise, “edition” will refer to the first edition, from now on. A second reason is that a core interest, here, is how the editorial work shaped Riemann’s text, which was largely accomplished in the first edition.
Dedekind and Weber’s editorial work was meticulous, mindful and even devoted, according to Elise Riemann. Their collaboration for this publication, which marked the beginning of almost forty years of friendship, was largely carried out in letters written from November 1st 1874 to the end of 1876. These letters have been preserved in Riemann’s archive (Cod. Ms. Bernhard Riemann, Niedersächsische Staats- und Universitätsbibliothek Göttingen) and in Dedekind’s (Cod. Ms. Richard Dedekind, Niedersächsische Staats- und Universitätsbibliothek Göttingen, and G 98:11–13, Archiv der Universitätsbibliothek Braunschweig),6Heinrich Weber’s archive seem, however, to have been lost [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) , p. 16]. and published in 2014 [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) ]. As most of their discussions appear in these letters, we have an extensive and detailed vision of the editorial process. Weber and Dedekind discussed every aspect of the edition, from the practical (e.g., the contract with Teubner, the copyrights, the advertisement of the book) to the scientific and philological (e.g., the choice of which texts to publish, their difficulties in understanding Riemann’s manuscripts, what kind of corrections or completions should be made before the publication). Indeed, a number of modifications were made to Riemann’s texts, from orthographical and typographical changes to the redaction of missing passages.
The process of editing Riemann’s Werke was thus a hands-on process, in which the editors were deeply involved in both the mathematical and philological aspects. Weber and Dedekind – and Hattendorff and Schwarz for some texts – engaged in a systematic verification of each and every one of Riemann’s texts, including those that had already been published. Some texts were, in fact, written by several hands: Riemann’s and the editor’s (for example, some parts of [20 B. Riemann, Sullo svolgimento del quoziente di duo serie ipergeometricho in frazione continua infinita. In [25], 1st ed. (1876), 400–406; 2nd ed. (1892); transl. En., 409–416. First published in 1863 ] are marked as being explicitly written by Schwarz). This raises questions on the genesis of the text and on the authorship.
All rights reserved
After the publication of the Dedekind-Weber correspondence, it became clear to me that there was, here, material to study how the edition of Riemann’s collected works was crafted. It also provides an opportunity to unfold parts of their mathematical activity which have been largely overlooked (until now!), and indeed to understand important aspects of Riemann’s influence on both mathematicians.7In 1882, Dedekind and Weber published Theorie der algebraischen Funktionen einer Veränderlichen (Theory of algebraic functions of one complex variable) in which they transfer Dedekind’s concepts of field, module and ideal from number theory to function theory to give a new definition of the Riemann surface and related notion, such as the genus. It also allows us to make connections with research in the history of text – how did the editing process shape the texts published? how did it shape the book itself? – and with the history of mathematical publishing.
Common interests in these questions led to collaboration between the History of Science, History of Text research group in the Laboratoire SPHERE (Université de Paris) and the Interdisziplinäre Zentrum für Wissenschafts- und Technikforschung (Bergische Universität Wuppertal) with the organisation of an ongoing series of workshops and seminars on the history of collected works as an editorial and scientific practice. Among our observations (some of which I will return to towards the end of this paper), the most relevant to the case of the Riemann edition are the following: texts published in collected works often bear the traces of the editorial work – maybe in more ways than we would expect – and for the editors, this was not solely an editorial or philological undertaking, but also a scholarly endeavour, and indeed one we seem to have overlooked so far.
The ongoing analysis of the edition of Riemann’s collected works is made possible by the documents available in Riemann’s archive,8The catalog is available here: hans.sub.uni-goettingen.de/nachlaesse/Riemann.pdf whose origins are described in [14 E. Neuenschwander, A brief report on a number of recently discovered sets of notes on Riemann’s lectures and on the transmission of the Riemann Nachlass. Hist. Mathematica15, 101–113 (1988) ], and in which most of the documents used by Weber and Dedekind are available.9See [30 D. E. Rowe, Göttingen’s SUB as Repository for the Papers of Distinguished Mathematicians. EMS Newsl.9, 39–44 (2016) ] for details on the development of Göttingen as an archive center. The only exception are the manuscripts that were the basis for [24 B. Riemann, Convergenz der p-fach unendlichen Theta-Reihe. In [25], 1st ed. (1876), 452–456; 2nd ed. (1892), 483–487; transl. En., 478–482. First published in 1876 , 27 B. Riemann, Zur Theorie der Abel’schen Functionen für den Fall p=3. In [25], 1st ed. (1876), 456–476; 2nd ed. (1892), 487–508; transl. En., 483–504. First published in 1876 ] which are in Schwarz’ archive at the Archiv der Berlin-Brandenburgischen Akademie der Wissenschaften. Dedekind’s archive also contains interesting material on his work as an editor (see below).
Since the 1970s and the great work done by Erwin Neuenschwander, many interesting historical works have been published using Riemann’s archive, a number of which will certainly be useful to the present project. The goal of this project is solely a critical analysis of the process of editing Riemann’s collected works, which comes along with a comparison of the original manuscripts and the published texts. The files in Riemann’s archive relating to the published texts contain thousands of pages (and around 500 pages in Dedekind’s archive). Most of the files contain several copies of the texts (usually by the editors, more rarely by Riemann), Riemann’s original texts and many of his drafts. Using a (semi-)automated approach to the transcription and comparison of the manuscripts with digital tools for handwritten text recognition and the tools developed by the CollEx-Persée project AMOr (www.collexpersee.eu/projet/amor/) should help manage these relatively large files.10Of course, for parts of this archive, in particular the letters, transcriptions are already available. In some of these files, the most challenging task might be to identify which documents were indeed used by the editors to produce the published text.
Shaping the individual texts
Heinrich Weber wrote an announcement of Riemann’s collected works for Koenigsberger and Zeuner’s Repertorium der literarischen Arbeiten aus dem Gebiete der reinen und angewandten Mathematik, in which he mentions the extent of the editorial work:
We only corrected some slight inaccuracies which were made known to the editor and could be seen as certain. Some additions, written according to Riemann’s manuscripts, and some necessary clarifications were placed in final notes. […] [T]he majority of [Riemann’s] posthumous writings contain only formulae with very little indications to find what link them. Hence, a lot of passages written only in a very fragmentary form had to be established as well as we could, and many others are still buried in his archive, for want of being deciphered. [36 H. Weber, Anzeige von Bernhard Riemann’s Gesammelte mathematische Werke und wissenschaftlicher Nachlass. Repertorium der literarischen Arbeiten aus dem Gebiete der reinen und angewandten MathematikI, 145–154 (1877) , pp. 7–8]
A similar statement can also be found in Weber’s preface in [25 B. Riemann, Gesammelte mathematische Werke und wissenschaftlicher Nachlass. Ed. by H. Weber in collaboration with R. Dedekind. Teubner, Leipzig. All references to this edition. Reprinted with Nachträge (1902), ed. M. Noether and W. Wirtinger, Teubner, Leipzig. Re-ed. (1953), Dover, New York. Re-ed. (1990), Springer/Teubner, Berlin. First published in 1876 , p. iv].
There are several types of modifications of Riemann’s original texts: the local, more or less significant changes to the texts, e.g., correcting an error, which are mentioned in notes; a number of such local changes, which are not mentioned in notes; and texts extracted from Riemann’s archive which are completed to a greater or lesser extent by the editor.11I have considered these questions in [11 E. Haffner, Insights into Dedekind and Weber’s edition of Riemann’s Gesammelte Werke. Math. Semesterber.64, 169–177 (2017) , 13 E. Haffner, L’édition des œuvres mathématiques au XIXieme siècle en Allemagne. L’exemple des Gesammelte Werke und wissenschaftlicher Nachlass de Bernhard Riemann. Philosophia Scientiæ22, 115–135 (2018) ]. An in-depth analysis of the edition of [17 B. Riemann, Fragmente über die Grenzfälle der elliptischen Modulfunctionen. In [25], 1st ed. (1876), 427–438; 2nd ed. (1892), 455–465; transl. En., 445–460. First published in 1852 ] is in progress and, as mentioned, so is a critical edition of Riemann’s texts. While the reader could expect to be able to identify clearly what was changed or added by the editors, this is not always the case. A number of changes are not clearly identified in any way, and can only be recognised as such by reading the editors’ correspondence or comparing the published texts with the manuscripts.12It is the case with [18 B. Riemann, Zur Theorie der Nobili’schen Farbenringe. In [25], 1st ed. (1876), 54–61; 2nd ed. (1892), 55–63. First published in 1854 ], whose edition I presented in [12 E. Haffner, Éditer les « horribles formules » de Riemann : un aperçu de l’édition de ses œuvres par Dedekind et Weber. Images des Mathématiques, CNRS, http://images.math.cnrs.fr/Editer-les-horribles-formules-de-Riemann-un-apercu-de-l-edition-de-ses-oeuvres (2018) ].
Of course, Weber and Dedekind were cautious with their corrections. In a letter from July 8, 1875, as he was proofreading Riemann’s famous Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse (On the number of primes less than a given magnitude) [19 B. Riemann, Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. In [25], 1st ed. (1876) 136–144; 2nd ed. (1892), 145–153; transl. En., 135–144. First published in 1859 ], Weber wrote to Dedekind:
Do you have any remarks on the work on primes? I have come to a difference from Riemann’s formula in the calculation, namely to the same one which Scheibner already noticed in his analysis of this work in Schlömilch’s journal. [[33 W. Scheibner, Ueber die Anzahl der Primzahlen unter einer beliebigen Grenze. Z. Mathematik und Physik5, 233–252 (1860) ]] Despite this, I am far from taking Riemann’s result to be incorrect, whose actual proof, as can be seen from a fragment of a letter, is not contained in the work at all. I do not dare to make any changes or additions. [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) , p. 71]
We don’t have any answer from Dedekind, but Weber later wrote again that he was finding “ instead of ” (as Scheibner had) but still didn’t dare to make any change or note, assuming that “it is probable that Riemann is right” but that he was missing the proof. The 1876 edition does not contain any correction or note, but there is a note by Weber in the 1892 edition, stating that
If one continues the computation indicated by Riemann, one finds in the formula instead of . It is very likely that this is but a typographical or printing mistake of in place of , indeed [sic].13This seems to be a typo correcting the typo, as , Weber meant to write “indeed ”. [25 B. Riemann, Gesammelte mathematische Werke und wissenschaftlicher Nachlass. Ed. by H. Weber in collaboration with R. Dedekind. Teubner, Leipzig. All references to this edition. Reprinted with Nachträge (1902), ed. M. Noether and W. Wirtinger, Teubner, Leipzig. Re-ed. (1953), Dover, New York. Re-ed. (1990), Springer/Teubner, Berlin. First published in 1876 , p. 155, 2nd edition 1892]
Changes can be even more important in texts extracted from Riemann’s archive. For some of them, the editors decided to write entire paragraphs themselves to complete Riemann’s original text before publication. Such changes raise questions as to the authorship of the texts, and the extent to which some of their content could be a result of edition as a collaborative enterprise. Some mathematicians in the years following the publication of Riemann’s collected works seemed to keep this aspect in mind, as suggested by a letter from Felix Klein to Henri Poincaré, sent on April 3rd, 1882, following a discussion on Riemann’s possible anticipation of some of Friedrich Schottky’s results:14Klein is, here, referring to [34 F. Schottky, Ueber die conforme Abbildung mehrfach zusammenhängender ebener Flächen. Inauguraldissertation, Schade (1875) ] and which was published in 1877 in the Journal für die reine und angewandte Mathematik, 83: 300–351, in which he studied conformal mappings of multiply connected domains, which he was the first to analyse systematically.
All rights reserved
[Regarding] Schottky, I would like to draw your attention to a posthumous essay in Riemann’s collected works, p. 413, where exactly corresponding ideas are developed. However, it will be difficult to establish how much the editor, Prof. Weber, has put into it. Riemann’s collected works appeared in 1876, Schottky’s dissertation in 1870, later as an essay in Borchardt’s Journal, 1877. (Letter from Klein, in [15 H. Poincaré, Œuvres de Henri Poincaré, tome XI. Gauthier-Villars, Paris (1956) , p. 53])
Klein is referring here to Gleichgewicht der Elektrizität auf Zylindern mit kreisförmigem Querschnitt und parallelen Axen (Equilibrium of electricity on cylinders with circular crosssection and parallel axes) [26 B. Riemann, Gleichgewicht der Elektrizität auf Zylindern mit kreisförmigem Querschnitt und parallelen Axen. In [25], 1st ed. (1876) 413–416, 2nd ed. (1892), 440–444; transl. En., 429–435. First published in 1876 ], which indeed deals with conformal mappings on a multiply connected surface. In a footnote, Weber states that
[t]here are no completed manuscripts of this and the following works by Riemann. They are composed of pages which, apart from a few hints, contain only formulae. [25 B. Riemann, Gesammelte mathematische Werke und wissenschaftlicher Nachlass. Ed. by H. Weber in collaboration with R. Dedekind. Teubner, Leipzig. All references to this edition. Reprinted with Nachträge (1902), ed. M. Noether and W. Wirtinger, Teubner, Leipzig. Re-ed. (1953), Dover, New York. Re-ed. (1990), Springer/Teubner, Berlin. First published in 1876 , p. 413]
Early in his correspondence with Dedekind, Weber mentioned that he would be “very interested” in being able to “decipher” the manuscripts on “the distribution of electricity on three spheres” [sic], which he hoped to be able to achieve since “on one of the sheets the results seem to be essentially in place” [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) , p. 62, letter from March 22, 1875]. As this last remark suggests, Riemann’s manuscripts in Cod. Ms. Riemann 5 contain many sheets with various states of development of his investigation. There are 27 pages by Riemann’s hand, for 4 pages of text by Weber, and certainly the material differences of each mathematician’s handwriting and use of paper do not account for such a large difference. In fact, many of Riemann’s notes contain similar computations, see Figure 2.
In addition, to put it bluntly, Weber’s version of Riemann’s research contains a lot more sentences and far fewer calculations. It is fairly easy to identify which formulae Weber included in his text. However, the sentences present in the published text are quite difficult to find in Riemann’s manuscripts. Thus, it seems that most of the redaction is by Weber, who completed and clarified Riemann’s text. He did not, here, correct or complete Riemann’s formulae – rather, he selected the relevant ones. It is, without a doubt, a text written by both Riemann and Weber.
In the available correspondence, Weber did not himself mention Schottky’s works. However, Schwarz wrote to Weber about Schottky’s dissertation on November 11, 1875 [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) , p. 362].15Schwarz wrote: “On Saturday and Sunday of last week, I was in Berlin and learned from Prof. Weierstrass of the dissertation of one of his students, a certain Schottky: ‘Über die conforme Abbildung mehrfach zusammenhängender Flächen’; if you do not not already know about this dissertation, please allow me to draw your attention to it. The results which are presented in this essay, are of great interest and scientific value; I myself will seek to obtain the dissertation in order to possess it.” Weber’s letters to Schwarz have been lost, and we do not know what he answered to this mention of Schottky’s paper. In January 1876, this text had, with seven others, already been sent to Teubner [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) , p. 95].
Another – and one of the most striking – examples of an extensive mathematical and editorial investment is the work done by Dedekind on “Fragmente über die Grenzfälle der elliptischen Modulfunctionen” (Fragments on the limit-cases of elliptic modular functions) [17 B. Riemann, Fragmente über die Grenzfälle der elliptischen Modulfunctionen. In [25], 1st ed. (1876), 427–438; 2nd ed. (1892), 455–465; transl. En., 445–460. First published in 1852 ].
All rights reserved
Dedekind started working on these manuscripts in February 1876. The lack of clarity of the notes, both from a material and a mathematical viewpoint, was so bad that editing them took Dedekind several weeks and led him to fear having nightmares (see [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) , pp. 101–104]). Over a dozen letters were exchanged between Dedekind and Weber from December 1875 to April 1876. Dedekind confided to Weber his difficulties in understanding and editing Riemann’s text (which he nicknamed, in his letters and in his own archive, “sehr blasses Manuskript von Riemann”, Riemann’s very pale manuscript, because it was written in pencil and had faded badly). Eventually, Dedekind made it through his deciphering of the manuscript, and was able to produce a complete transcription of Riemann’s notes. He verified each formula and corrected them when necessary, but did not make any additions. In addition, he wrote a 10-page commentary containing original research [4 R. Dedekind, Erläuterungen zu den vorstehenden Fragmenten. In [25], 1st ed. (1876) 438–448, 2nd ed. (1892), 466–479; transl. En., 461–474. First published in 1876 ].
These Fragments consider properties of Jacobi series in elliptic function theory. Without entering into any detail, Dedekind interpreted Riemann’s formulae as the study of the logarithm of some modular functions at the limits of their domain of definition. In the collected works, he stated:
The time of writing of the first of the two fragments (September 1852) makes it likely that Riemann, while working on his memoir On the representation of a function by a trigonometric series, was looking for examples of functions with infinitely many discontinuities in each interval. Perhaps the second investigation, which occurs on the barely legible sheet, has the same object.16[1 J. Arias-De-Reyna, Riemann’s Fragment on Limit Values of Elliptic Modular Functions. Ramanujan J.8, 57–123 (2004) ] disagrees with this interpretation. Hopefully, the manuscripts hold some elements to answer this question. [4 R. Dedekind, Erläuterungen zu den vorstehenden Fragmenten. In [25], 1st ed. (1876) 438–448, 2nd ed. (1892), 466–479; transl. En., 461–474. First published in 1876 , p. 438]
In Cod. Ms. Riemann 14, we find the 15 pages of Riemann’s original manuscript, two handwritten transcriptions, the handwritten text for Dedekind’s 1876 commentary and the version sent to the editor, some notes written by Weber, the 1876 letters between Dedekind and Weber relating to that text, and one of Dedekind’s early works on elliptic functions, which he intended to use to understand Riemann’s ideas and likely sent to Weber with one of his letters.
All rights reserved
All rights reserved
All rights reserved
The most exceptional documents can be found in Dedekind’s archive. In Cod. Ms. Dedekind XI 11-1, XI 11-2, XII 4,17Cod. Ms. Dedekind XII 4 is mistakenly listed as referring to [23 B. Riemann, Beispiele von Flächen kleinsten Inhalts bei gegebener Begrenzung. In [25], 417–426. First published in 1876 ] in the Göttingen catalog, because Dedekind refers to the text using the numbering in the table of contents in the 1892 reedition of Riemann’s collected works. The contents of the file are, however, undoubtedly related to [17 B. Riemann, Fragmente über die Grenzfälle der elliptischen Modulfunctionen. In [25], 1st ed. (1876), 427–438; 2nd ed. (1892), 455–465; transl. En., 445–460. First published in 1852 ]. In exploring these documents, I have greatly benefited from Walter Strobl’s help. we find several hundred pages of notes written solely by Dedekind. There, we see the progression in his understanding of Riemann’s texts and of the writing of his 1876 and 1892 commentaries, as well as continuations of his research on the subject. These pages show the breadth and depth of the mathematical reflections developed by Dedekind for his editorial work. In addition to computations following Riemann’s manuscripts and trying to obtain again Riemann’s results, Dedekind developed his own approach to the subject, which ended up being his only way to verify Riemann’s results. For this, he drew comparisons between both approaches, at some points relying only on the correspondences between numerical examples, and eventually systematically exploring the correspondences between his and Riemann’s results. This research was also the basis for his commentaries, of which we find several drafts in the archive. Both Dedekind’s commentaries, although entitled “Explanation on the preceding fragments” do not actually explain what Riemann was trying to do, rather they present:
a very interesting application related to the so-called theory of the infinitely many forms of the theta-functions, namely the determination of the constants appearing via transformations of first degree, which as is known, were reduced by Jacobi and Hermite to Gauss sums, and thus to the theory of quadratic residues. The following commentary illustrates these relationships. [4 R. Dedekind, Erläuterungen zu den vorstehenden Fragmenten. In [25], 1st ed. (1876) 438–448, 2nd ed. (1892), 466–479; transl. En., 461–474. First published in 1876 , p. 438]
In particular, it is there that Dedekind introduced what we today call the Dedekind eta function.18The Dedekind eta function is a modular form defined on the upper-half part of the complex plane by [4 R. Dedekind, Erläuterungen zu den vorstehenden Fragmenten. In [25], 1st ed. (1876) 438–448, 2nd ed. (1892), 466–479; transl. En., 461–474. First published in 1876 , p. 438].
All rights reserved
Shaping the book and shaping the image of the editee
The way in which a book such as a mathematician’s collected works is constructed – which texts are chosen to be in this publication; whether unpublished manuscripts are selected and if so, which ones, and how they are published; whether a critical apparatus is added and which one; how texts are organised and, when applicable, how the multiple volumes are themselves organised, etc. – shapes the image of the editee presented to the readers. Indeed, such choices are a reflection of the editor’s own idea of the editee’s work, and of what they want to showcase of it.19Note that this is also an important point regarding the role that individuals play in editing their own work or in supervising such an edition (e.g., Poncelet, Weierstrass). The shaping of the book is, in fact, the shaping of the vector of circulation of the editee’s works. Without undue generalization on the possibility of biases on the part of editors, the history of mathematics gives us several examples in which mathematicians works were largely reconstructed by the editors.
The selection of which texts are deemed suitable for publication plays a significant role in such a reconstruction of the works of the editee. Through these choices, the editors impose their own criteria and their own values on the editee’s texts. And it is all the more pregnant regarding the choice of excerpts from the author’s archives, as there are few ways of knowing whether the author had any intention of publishing these texts, or why they didn’t. As such, our vision of the editee’s work can be restricted to the editors’ reading of it. And this contributes, to a certain extent, to a mythologised history of mathematics.
Let me give three examples, which are not Riemann’s collected works, in which this happened. A first, and very striking, example is the edition of Leibniz’s works, which was mentioned in David Rabouin’s recent paper in the archive series on Leibniz’s archives [16 D. Rabouin, Exploring Leibniz’s Nachlass at the Niedersächsische Landesbibliothek in Hanover. EMS Newsl.6, 17–23 (2020) ], in which he explains how “some texts edited by Gerhardt and Couturat have turned out to be mere artefacts”. A second example is the edition of Gauss’ collected works, a gigantic enterprise that took several decades, first directed by Ernst Schering, then by Felix Klein (see [10 C. Goldstein, N. Schappacher and J. Schwermer (eds.), The Shaping of Arithmetic after C. F. Gauss’s Disquisitiones Arithmeticae. Springer, Berlin, Heidelberg, New York (2007) , pp. 67–68] and [30 D. E. Rowe, Göttingen’s SUB as Repository for the Papers of Distinguished Mathematicians. EMS Newsl.9, 39–44 (2016) ]). Maarten Bullynck showed, in a talk at the Laboratoire SPHERE (Université de Paris), how the edition of Gauss’ collected works was one of the elements of Klein’s retrospective reconstruction of the so-called Göttingen tradition in mathematics. My third example is the edition of Dedekind’s collected works by Emmy Noether, Øystein Ore and Robert Fricke in 1930–1932. The three volumes are organized as follows: the first two contain Dedekind’s mathematical papers arranged in chronological order with some extracts from his archive, the third contains his foundational essays on real and natural numbers, partial reproductions of his algebraic number theory20[3 R. Dedekind, Über die Composition der binären quadratischen Formen, Xth Supplement. In Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie, 2nd ed., 380–497 (1871). Partially repr. in [7] III, pages 223–262. , 6 R. Dedekind, Über die Theorie der algebraischen Zahlen, XIth Supplement. In Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie, 4th edition, 434–657 (1894). Repr. in [7] III, 1–222. ] which were respectively published as Supplements to the 1871 and 1894 editions of Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie and [5 R. Dedekind, Théorie des nombres entiers algébriques. Published in five parts in Bulletin des Sciences Astronomiques et Mathématiques: BSAM 11 (1876), pages 278–288; BSAM Sér. 2(1):1 (1877), pages 17–41, 69–92, 144–164, and 207–248. Partially repr. in [7] III 262–296. First published in 1876–1877 ] which was published in French and later as a Supplement to the 1879 edition of Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie. In these papers, Dedekind introduced and developed the concepts of field and ideal. and more extracts from his archive. This arrangement creates two illusions. First, that of a difference of status between Dedekind’s ‘mathematical’ and his ‘foundational’ papers, a distinction he did not make himself. Second, the partial reproduction of his algebraic number theory completely disconnects this research from its number-theoretical context and, in fact, excludes its more traditional parts. These choices were likely guided by the editors considering Dedekind as a precursor of the modern structural algebra and certainly participated in perpetuating this retrospective reading of his work.
While in many of these cases we can only observe the choices made by the editors and make assumptions about their intentions, for Riemann’s collected works, the letters exchanged between Dedekind and Weber offer us a considerable amount of information on these questions, making it a rather exceptional case study. Their exchanges indeed tell us which texts were dismissed as not ‘worthy’ of being published, and the criteria that presided on their choices. Let me sum up the main criteria for Dedekind and Weber’s choices:
A text had to be (of course) scientifically sound and generally correct – as correct as possible but the scientific interest came first;
it had to be understandable – even if this sometimes meant that the editors had to make the text more understandable than the way it was left by Riemann;
it had to be representative of Riemann’s research, it had to have a recognisable place in his overall intellectual production;
it had to (of course) give a flattering image of Riemann;
it had to fit into the scientific and philosophical context of the time, to ensure that it would be well received by the scientific community.
Any process of choice is subjective – it would be difficult to think of any editions that are completely unbiased. But in the case of Riemann’s collected works, we can pinpoint some of the effects that the editors’ choices had. The question of whether the texts in Riemann’s collected works can be attributed solely to him, raised by Klein, is one of them.
Another issue is the extent to which the image of Riemann provided by the collected works might have been shaped by what the editors thought it should be. Dedekind was very vocal about seeing Riemann as the best representative of how mathematical definitions and proofs should be grounded on conceptual, fundamental characteristics rather than on computations and notations. He considered himself as following these methodological guidelines. Thus, was born the narrative of a tradition of “conceptual mathematics” in Göttingen, which was later largely continued by Klein and Hilbert’s group. These highly influential mathematicians developed a culture in Göttingen which has been described as largely relying on “nostrification” (see [2 L. Corry, David Hilbert and his mathematical workilbert and the Axiomatization of Physics (1898–1918): From Grundlagen der Geometrie to Grundlagen der Physik. Archimedes (Dordrecht), Springer (2004) ]), a tendency to reinterpret other people’s thoughts so that they would fit their own current picture of the domain. The desire, strongly expressed by Klein, to create a new kind of scientific institution might have led to the reconstruction of a history, an inheritance, which selected and overemphasized some isolated ideas (see [10 C. Goldstein, N. Schappacher and J. Schwermer (eds.), The Shaping of Arithmetic after C. F. Gauss’s Disquisitiones Arithmeticae. Springer, Berlin, Heidelberg, New York (2007) ] and [31 D. E. Rowe, A Richer Picture of Mathematics. The Göttingen Tradition and Beyond. Springer, Berlin, Heidelberg, New York (2018) ]).
This goes, of course, beyond the mere publication of collected works. It is however tangible in the French translation of Riemann’s collected works, published in 1898, edited and translated by Léonce Laugel. He chose to exclude not only the papers published in French and Latin, but also most of the papers not related to mathematics (i.e., all papers on physics and the philosophical fragments). He replaced Weber’s preface with a preface by Charles Hermite (1822–1901) and added the translation of a talk given by Klein, both of which embrace the idea of Riemann as avoiding computations and relying solely on concepts and a “brilliant power of thought and [an] anticipatory imagination [which] led him frequently to take very great steps that others could not so easily follow”, as Dedekind wrote of Riemann in his biography.
Later commentators did not all agree with the image of Riemann that this narrative participated in popularizing among mathematicians. Carl Siegel, who famously discovered the Riemann–Siegel formula in Riemann’s archive wrote:
The legend according to which Riemann found his mathematical results through grand general ideas without requiring the formal tools of analysis, is not as widely believed today as it was during Felix Klein’s lifetime. Just how strong Riemann’s analytic technique was is especially clearly shown by the derivation and transformation of his asymptotic series for . [35 C. L. Siegel, Über Riemanns Nachlass zur analytischen Zahlentheorie. Quell. Stud. Gesch. Math.2, 45–80 (1932) , p. 276] (translated in [9 H. M. Edwards, The Algorithmic Side of Riemann’s Mathematics. In A Celebration of the Mathematical Legacy of Raoul Bott, ed. by R. Bott and P. Kotiuga, CRM Proceedings & Lecture Notes, American Mathematical Society, Providence (2010) , p. 67])
This was also defended by the historian Harold M. Edwards, in [9 H. M. Edwards, The Algorithmic Side of Riemann’s Mathematics. In A Celebration of the Mathematical Legacy of Raoul Bott, ed. by R. Bott and P. Kotiuga, CRM Proceedings & Lecture Notes, American Mathematical Society, Providence (2010) ], who argued for a strong – albeit maybe hidden in drafts – algorithmic component in Riemann’s mathematics. Edwards showed how Riemann, while he may have been “primarily interested in grand general abstract concepts,” on several occasions “did not venture into these higher realms without doing a lot of serious computation to lay the groundwork for his flights.” [9 H. M. Edwards, The Algorithmic Side of Riemann’s Mathematics. In A Celebration of the Mathematical Legacy of Raoul Bott, ed. by R. Bott and P. Kotiuga, CRM Proceedings & Lecture Notes, American Mathematical Society, Providence (2010) , p. 64].21Note that Arias-de-Reyna also claims that Dedekind’s misinterpretation of Riemann’s fragments on modular elliptic functions is related to his overlooking the importance of computations for Riemann. These observations are confirmed by Riemann’s archive, in particular by the many parts that remain unpublished – which Carl Siegel, of course, knew very well.
This leads me to one last potential issue, or more exactly to a limitation any editor would face with the manuscripts of a mathematician such as Riemann: understanding their content. As Carl Siegel’s work on the Riemann–Siegel formula has shown, Riemann’s archive contained, and maybe still contains, important unpublished (even if not fully developed) results that escaped Weber’s and Dedekind’s attention. This shows the extent to which it can be useful and fruitful to revisit mathematicians’ archives.
Acknowledgements This work was supported by a public grant as part of the Investissement d’avenir project, reference ANR-11-LABX-0056-LMH, LabEx LMH.
- 1
At this time, a considerable number of projects of publishing collected works were launched in France, Germany, Italy, the United Kingdom … The publisher B. G. Teubner, created in 1811 in Leipzig, which specialised in scientific editions (broadly construed, i.e., philology, history, mathematics, physics, etc.), was one of the leading publishers for this type of book in Germany. – Steven W. Rockey from Cornell University published a very complete list of collected works in mathematics: mathematics.library.cornell.edu/about-collected-works/.
- 2
[22 B. Riemann, Ueber die Fläche vom kleinsten Inhalt bei gegebener Begrenzung. In [25], 1st ed. (1876) 283–315, 2nd ed. (1892), 301–335; transl. En., 387–322. First published in 1867 ] was edited by Karl Hattendorff (1834–1882), [21 B. Riemann, Mechanik des Ohres. In [25], 1st ed. (1876), 316–330; 2nd ed. (1892), 338–352. First published in 1867 ] by Ernst Schering (1824–1889) and Friedrich Henle (1809–1885), the other texts presumably by Dedekind. – A note on the dates of the publications: when it is possible to date Riemann’s texts, these are the given dates; when it is not, the dates are that of the first publication.
- 3
Maybe a less famous name than Riemann, Clebsch and Dedekind, Heinrich Weber was a prominent mathematician throughout his career. He studied in Heidelberg, Leipzig and Königsberg. He taught in Heidelberg, Zürich, Königsberg (where he taught number theory to Hilbert and Minkowski), Berlin, Marburg, Göttingen, and Strasbourg. He worked extensively on complex function theory, number theory, and algebra. Among several important contributions to the latter, his Lehrbuch der Algebra was to be the main reference for teaching algebra in the German speaking world until the publication of Van der Waerden’s Moderne Algebra in 1930. He also made contributions to mathematical physics, and published Die partiellen Differentialgleichungen der mathematischen Physik nach Riemann’s Vorlesungen, which was, for a long time, the only reference for Riemann’s mathematical physics. Weber was also actively involved in the mathematical community, for example he was a member of the editorial committee of the Mathematische Annalen and a founding member of the Deutsche Mathematiker-Vereinigung.
- 4
In 1990, the 1902 edition was reprinted along with additions. A French translation appeared in 1898, translated by Léonce Laugel and published by Gauthiers-Villars (see p. Shaping the book and shaping the image of the editee). The first English translation appeared in 2004 [29 B. Riemann, Collected Papers. Kendrick Press, Heber City (2004) ].
- 5
Unless stated otherwise, “edition” will refer to the first edition, from now on.
- 6
Heinrich Weber’s archive seem, however, to have been lost [32 K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014) , p. 16].
- 7
In 1882, Dedekind and Weber published Theorie der algebraischen Funktionen einer Veränderlichen (Theory of algebraic functions of one complex variable) in which they transfer Dedekind’s concepts of field, module and ideal from number theory to function theory to give a new definition of the Riemann surface and related notion, such as the genus.
- 8
The catalog is available here: hans.sub.uni-goettingen.de/nachlaesse/Riemann.pdf
- 9
See [30 D. E. Rowe, Göttingen’s SUB as Repository for the Papers of Distinguished Mathematicians. EMS Newsl.9, 39–44 (2016) ] for details on the development of Göttingen as an archive center.
- 10
Of course, for parts of this archive, in particular the letters, transcriptions are already available.
- 11
I have considered these questions in [11 E. Haffner, Insights into Dedekind and Weber’s edition of Riemann’s Gesammelte Werke. Math. Semesterber.64, 169–177 (2017) , 13 E. Haffner, L’édition des œuvres mathématiques au XIXieme siècle en Allemagne. L’exemple des Gesammelte Werke und wissenschaftlicher Nachlass de Bernhard Riemann. Philosophia Scientiæ22, 115–135 (2018) ]. An in-depth analysis of the edition of [17 B. Riemann, Fragmente über die Grenzfälle der elliptischen Modulfunctionen. In [25], 1st ed. (1876), 427–438; 2nd ed. (1892), 455–465; transl. En., 445–460. First published in 1852 ] is in progress and, as mentioned, so is a critical edition of Riemann’s texts.
- 12
It is the case with [18 B. Riemann, Zur Theorie der Nobili’schen Farbenringe. In [25], 1st ed. (1876), 54–61; 2nd ed. (1892), 55–63. First published in 1854 ], whose edition I presented in [12 E. Haffner, Éditer les « horribles formules » de Riemann : un aperçu de l’édition de ses œuvres par Dedekind et Weber. Images des Mathématiques, CNRS, http://images.math.cnrs.fr/Editer-les-horribles-formules-de-Riemann-un-apercu-de-l-edition-de-ses-oeuvres (2018) ].
- 13
This seems to be a typo correcting the typo, as , Weber meant to write “indeed ”.
- 14
Klein is, here, referring to [34 F. Schottky, Ueber die conforme Abbildung mehrfach zusammenhängender ebener Flächen. Inauguraldissertation, Schade (1875) ] and which was published in 1877 in the Journal für die reine und angewandte Mathematik, 83: 300–351, in which he studied conformal mappings of multiply connected domains, which he was the first to analyse systematically.
- 15
Schwarz wrote: “On Saturday and Sunday of last week, I was in Berlin and learned from Prof. Weierstrass of the dissertation of one of his students, a certain Schottky: ‘Über die conforme Abbildung mehrfach zusammenhängender Flächen’; if you do not not already know about this dissertation, please allow me to draw your attention to it. The results which are presented in this essay, are of great interest and scientific value; I myself will seek to obtain the dissertation in order to possess it.”
- 16
[1 J. Arias-De-Reyna, Riemann’s Fragment on Limit Values of Elliptic Modular Functions. Ramanujan J.8, 57–123 (2004) ] disagrees with this interpretation. Hopefully, the manuscripts hold some elements to answer this question.
- 17
Cod. Ms. Dedekind XII 4 is mistakenly listed as referring to [23 B. Riemann, Beispiele von Flächen kleinsten Inhalts bei gegebener Begrenzung. In [25], 417–426. First published in 1876 ] in the Göttingen catalog, because Dedekind refers to the text using the numbering in the table of contents in the 1892 reedition of Riemann’s collected works. The contents of the file are, however, undoubtedly related to [17 B. Riemann, Fragmente über die Grenzfälle der elliptischen Modulfunctionen. In [25], 1st ed. (1876), 427–438; 2nd ed. (1892), 455–465; transl. En., 445–460. First published in 1852 ]. In exploring these documents, I have greatly benefited from Walter Strobl’s help.
- 18
The Dedekind eta function is a modular form defined on the upper-half part of the complex plane by [4 R. Dedekind, Erläuterungen zu den vorstehenden Fragmenten. In [25], 1st ed. (1876) 438–448, 2nd ed. (1892), 466–479; transl. En., 461–474. First published in 1876 , p. 438].
- 19
Note that this is also an important point regarding the role that individuals play in editing their own work or in supervising such an edition (e.g., Poncelet, Weierstrass).
- 20
[3 R. Dedekind, Über die Composition der binären quadratischen Formen, Xth Supplement. In Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie, 2nd ed., 380–497 (1871). Partially repr. in [7] III, pages 223–262. , 6 R. Dedekind, Über die Theorie der algebraischen Zahlen, XIth Supplement. In Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie, 4th edition, 434–657 (1894). Repr. in [7] III, 1–222. ] which were respectively published as Supplements to the 1871 and 1894 editions of Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie and [5 R. Dedekind, Théorie des nombres entiers algébriques. Published in five parts in Bulletin des Sciences Astronomiques et Mathématiques: BSAM 11 (1876), pages 278–288; BSAM Sér. 2(1):1 (1877), pages 17–41, 69–92, 144–164, and 207–248. Partially repr. in [7] III 262–296. First published in 1876–1877 ] which was published in French and later as a Supplement to the 1879 edition of Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie. In these papers, Dedekind introduced and developed the concepts of field and ideal.
- 21
Note that Arias-de-Reyna also claims that Dedekind’s misinterpretation of Riemann’s fragments on modular elliptic functions is related to his overlooking the importance of computations for Riemann.
References
- J. Arias-De-Reyna, Riemann’s Fragment on Limit Values of Elliptic Modular Functions. Ramanujan J.8, 57–123 (2004)
- L. Corry, David Hilbert and his mathematical workilbert and the Axiomatization of Physics (1898–1918): From Grundlagen der Geometrie to Grundlagen der Physik. Archimedes (Dordrecht), Springer (2004)
- R. Dedekind, Über die Composition der binären quadratischen Formen, Xth Supplement. In Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie, 2nd ed., 380–497 (1871). Partially repr. in [7] III, pages 223–262.
- R. Dedekind, Erläuterungen zu den vorstehenden Fragmenten. In [25], 1st ed. (1876) 438–448, 2nd ed. (1892), 466–479; transl. En., 461–474. First published in 1876
- R. Dedekind, Théorie des nombres entiers algébriques. Published in five parts in Bulletin des Sciences Astronomiques et Mathématiques: BSAM 11 (1876), pages 278–288; BSAM Sér. 2(1):1 (1877), pages 17–41, 69–92, 144–164, and 207–248. Partially repr. in [7] III 262–296. First published in 1876–1877
- R. Dedekind, Über die Theorie der algebraischen Zahlen, XIth Supplement. In Lejeune-Dirichlet’s Vorlesungen über Zahlentheorie, 4th edition, 434–657 (1894). Repr. in [7] III, 1–222.
- R. Dedekind, Gesammelte mathematische Werke. 3 vols. Ed. by Robert Fricke, Emmy Noether and Öystein Ore. Vieweg, Braunschweig, (1930–1932). Re-ed. Chelsea Publishing Co., New York (1968)
- P. Dugac, Richard Dedekind et les fondements des mathématiques. Vrin, Paris (1976)
- H. M. Edwards, The Algorithmic Side of Riemann’s Mathematics. In A Celebration of the Mathematical Legacy of Raoul Bott, ed. by R. Bott and P. Kotiuga, CRM Proceedings & Lecture Notes, American Mathematical Society, Providence (2010)
- C. Goldstein, N. Schappacher and J. Schwermer (eds.), The Shaping of Arithmetic after C. F. Gauss’s Disquisitiones Arithmeticae. Springer, Berlin, Heidelberg, New York (2007)
- E. Haffner, Insights into Dedekind and Weber’s edition of Riemann’s Gesammelte Werke. Math. Semesterber.64, 169–177 (2017)
- E. Haffner, Éditer les « horribles formules » de Riemann : un aperçu de l’édition de ses œuvres par Dedekind et Weber. Images des Mathématiques, CNRS, http://images.math.cnrs.fr/Editer-les-horribles-formules-de-Riemann-un-apercu-de-l-edition-de-ses-oeuvres (2018)
- E. Haffner, L’édition des œuvres mathématiques au XIXieme siècle en Allemagne. L’exemple des Gesammelte Werke und wissenschaftlicher Nachlass de Bernhard Riemann. Philosophia Scientiæ22, 115–135 (2018)
- E. Neuenschwander, A brief report on a number of recently discovered sets of notes on Riemann’s lectures and on the transmission of the Riemann Nachlass. Hist. Mathematica15, 101–113 (1988)
- H. Poincaré, Œuvres de Henri Poincaré, tome XI. Gauthier-Villars, Paris (1956)
- D. Rabouin, Exploring Leibniz’s Nachlass at the Niedersächsische Landesbibliothek in Hanover. EMS Newsl.6, 17–23 (2020)
- B. Riemann, Fragmente über die Grenzfälle der elliptischen Modulfunctionen. In [25], 1st ed. (1876), 427–438; 2nd ed. (1892), 455–465; transl. En., 445–460. First published in 1852
- B. Riemann, Zur Theorie der Nobili’schen Farbenringe. In [25], 1st ed. (1876), 54–61; 2nd ed. (1892), 55–63. First published in 1854
- B. Riemann, Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. In [25], 1st ed. (1876) 136–144; 2nd ed. (1892), 145–153; transl. En., 135–144. First published in 1859
- B. Riemann, Sullo svolgimento del quoziente di duo serie ipergeometricho in frazione continua infinita. In [25], 1st ed. (1876), 400–406; 2nd ed. (1892); transl. En., 409–416. First published in 1863
- B. Riemann, Mechanik des Ohres. In [25], 1st ed. (1876), 316–330; 2nd ed. (1892), 338–352. First published in 1867
- B. Riemann, Ueber die Fläche vom kleinsten Inhalt bei gegebener Begrenzung. In [25], 1st ed. (1876) 283–315, 2nd ed. (1892), 301–335; transl. En., 387–322. First published in 1867
- B. Riemann, Beispiele von Flächen kleinsten Inhalts bei gegebener Begrenzung. In [25], 417–426. First published in 1876
- B. Riemann, Convergenz der p-fach unendlichen Theta-Reihe. In [25], 1st ed. (1876), 452–456; 2nd ed. (1892), 483–487; transl. En., 478–482. First published in 1876
- B. Riemann, Gesammelte mathematische Werke und wissenschaftlicher Nachlass. Ed. by H. Weber in collaboration with R. Dedekind. Teubner, Leipzig. All references to this edition. Reprinted with Nachträge (1902), ed. M. Noether and W. Wirtinger, Teubner, Leipzig. Re-ed. (1953), Dover, New York. Re-ed. (1990), Springer/Teubner, Berlin. First published in 1876
- B. Riemann, Gleichgewicht der Elektrizität auf Zylindern mit kreisförmigem Querschnitt und parallelen Axen. In [25], 1st ed. (1876) 413–416, 2nd ed. (1892), 440–444; transl. En., 429–435. First published in 1876
- B. Riemann, Zur Theorie der Abel’schen Functionen für den Fall p=3. In [25], 1st ed. (1876), 456–476; 2nd ed. (1892), 487–508; transl. En., 483–504. First published in 1876
- B. Riemann, Verbreitung der Wärme im Ellipsoid. In [25], 2nd ed. (1892), 437–439; transl. En., 425–428. First published in 1892
- B. Riemann, Collected Papers. Kendrick Press, Heber City (2004)
- D. E. Rowe, Göttingen’s SUB as Repository for the Papers of Distinguished Mathematicians. EMS Newsl.9, 39–44 (2016)
- D. E. Rowe, A Richer Picture of Mathematics. The Göttingen Tradition and Beyond. Springer, Berlin, Heidelberg, New York (2018)
- K. Scheel, Der Briefwechsel Richard Dedekind – Heinrich Weber. 5, Abhandlungen der Akademie der Wissenschaften in Hamburg (5), De Gruyter Oldenbourg, Hamburg (2014)
- W. Scheibner, Ueber die Anzahl der Primzahlen unter einer beliebigen Grenze. Z. Mathematik und Physik5, 233–252 (1860)
- F. Schottky, Ueber die conforme Abbildung mehrfach zusammenhängender ebener Flächen. Inauguraldissertation, Schade (1875)
- C. L. Siegel, Über Riemanns Nachlass zur analytischen Zahlentheorie. Quell. Stud. Gesch. Math.2, 45–80 (1932)
- H. Weber, Anzeige von Bernhard Riemann’s Gesammelte mathematische Werke und wissenschaftlicher Nachlass. Repertorium der literarischen Arbeiten aus dem Gebiete der reinen und angewandten MathematikI, 145–154 (1877)
Cite this article
Emmylou Haffner, The edition of Bernhard Riemann’s collected works: Then and now. Eur. Math. Soc. Mag. 120 (2021), pp. 29–39
DOI 10.4171/MAG/18