The present column is devoted to probability theory.
I Six new problems – solutions solicited
Solutions will appear in a subsequent issue.
284
Let be a finite set and . For a finite path on , we let , and for , we let
We call , where is the last index found by the algorithm, the partial loop erasure (PLE) of .
Let be a discrete-time irreducible Markov chain on a finite set , and let and . Prove that
where means that both sides have the same law.
Shiping Cao (Department of Mathematics, University of Washington, Seattle, USA)
This problem is a simplified version of Theorem 1 of my recent paper: S. Cao, Scaling limits of loop-erased Markov chains on resistance spaces via a partial loop-erasing procedure. Adv. Math.435, part B, article no. 109382 (2023).
285
The following democratic process is implemented in a population of sheep during a Yes/No referendum. At the initial time , sheep are pro-Yes, and sheep are pro-No. At each time , a sheep is randomly chosen (independently of what happened before) and it bleeps its opinion. Instantly, a sheep from the opposite camp (if at least one remains) switches its opinion. The process stops when a consensus is reached.
We denote by the probability that “Yes” wins when starting with pro-Yes sheep in the population. Of course, , , and, due to the symmetry of the problem, .
Question.
Find a simple expression for . (In particular, this expression should allow you to estimate very easily the evolution of this probability when starting from a very small majority, i.e., estimate for different sequences .)
Lucas Gerin (CMAP, École Polytechnique, Palaiseau, France)
286
Let and consider the transition probability density from a point after a time of a Brownian motion on the non-negative real line with reflecting boundary conditions; in particular, is the weak solution of the following initial value problem with Robin boundary condition:
for all and ;
for all , where the derivative at the origin is the one-sided right derivative;
for all bounded continuous functions and .
Prove that the solution is given by
for any and , where is complementary error function and is the partial derivative with respect to .
Mario Kieburg (School of Mathematics and Statistics, University of Melbourne, Parkville, Melbourne, Australia)
287
We place different pairs of socks in a tumble dryer. When the dryer has thoroughly mixed the socks, they are taken out one by one. If a sock is the partner of one of the socks on the sorting table, both are removed, otherwise it is put on the table until its partner emerges from the dryer. For , let be the number of socks on the table when the th sock is taken from the dryer. With , the random path is a Dyck path. Recall that a path is called a Dyck path if , for and .
The number of Dyck paths of a given length is given by the Catalan numbers, but not all Dyck paths come up with the same probability in the sock sorting process. For example, for there are two Dyck paths, and . The former has probability and the latter . The problem is now, given a Dyck path of arbitrary length, to find a formula for the probability
Peter Mörters (University of Cologne, Germany)
288
In a university hospital, there are 9 major medical departments performing surgery. The cardiology unit performs 21% of all surgeries conducted hospital-wide, with 5% of total cardiac surgeries occurring at least twice a day. A total of 30 patients are assigned to surgery. Assuming that surgeries are equally likely on any given day of the year, if two or more surgeries occur on the same day, what is the probability that they are assigned to the cardiology unit?
Gaetano Valenza (Bioengineering and Robotics Research Center “E. Piaggio” & Department of Information Engineering, School of Engineering, University of Pisa, Italy)
289
It is the king’s birthday, and he decides to please the republican sentiments in the population and release some prisoners who are held for their republican views. The prisoners all have equally excellent rational skills and are placed in separate castles, so that they are unable to speak and communicate with each other. The king decides to challenge the prisoners and gives each of them a coin. Within a quarter of an hour, each of them, say prisoners, has to decide whether to toss the coin or not. If at least one coin is tossed and all coins being tossed show head, all prisoners are released, otherwise none of them are. The king believes the prisoners have a slim chance of being released. But is that so? What is the probability that they all are released? The prisoners are told the number .
Carsten Wiuf (Department of Mathematical Sciences, University of Copenhagen, Denmark)
II Open problems
by Van Vu (Department of Mathematics, Yale University, USA)
Open problems on random matrices
Let be a random matrix of size whose entries are iid random variables (with probability each). It is known that most of the eigenvalues of this matrix, with high probability, are complex and distribute by the circular law [2 T. Tao and V. Vu, From the Littlewood–Offord problem to the circular law: universality of the spectral distribution of random matrices. Bull. Amer. Math. Soc. (N.S.) 46, 377–396 (2009) ]. The question here is that how many are real.
The following conjecture is motivated by my joint work with T. Tao in [3 T. Tao and V. Vu, Random matrices: Universality of local spectral statistics of non-Hermitian matrices. Ann. Probab. 43, 782–874 (2015) ].
290*. Conjecture (real eigenvalues)
has, with probability , real eigenvalues.
Edelman, Kostlan, and Shub [1 A. Edelman, E. Kostlan and M. Shub, How many eigenvalues of a random matrix are real? J. Amer. Math. Soc. 7, 247–267 (1994) ] obtained a precise formula for the expectation of the number of real eigenvalues for a Gaussian matrix, which is of order . In [3 T. Tao and V. Vu, Random matrices: Universality of local spectral statistics of non-Hermitian matrices. Ann. Probab. 43, 782–874 (2015) ], Tao and Vu proved that the same formula holds (in the asymptotic sense) for certain random matrices with entries , as a part of a Four Moment Theorem for non-symmetric matrices. However, we cannot extend the proof to . As a matter of fact, it is not known that with high probability, has at least 2 real roots.
The next problem bears some resemblance to the famous “rigidity” problem in computer science. Given a matrix , let denote the minimum number of entries we need to switch (from 1 to and vice versa) in order to make singular. Thus, can be seen as the resilience of against an effort to reduce its rank. It is easy to show that is, with high probability, at most , it typically takes this many switches to make the first two rows of the matrix equal.
291*. Conjecture (rank resilience)
With probability , .
For more discussion and related problems, we refer to [4 V. H. Vu, Recent progress in combinatorial random matrix theory. Probab. Surv. 18, 179–200 (2021) ].
III Solutions
276
Consider the tiling of the plane by regular hexagon tiles, with centers in the lattice of all -linear combinations of the vectors and . Glue all but finitely many tiles into position, remove the unglued tiles to form a region, discard some of these tiles, and arrange the remaining unglued tiles in the region without rotating them, in arbitrary positions such that none of the tiles overlap. Is there a way to slide the unglued tiles within the region, keeping them upright and non-overlapping, so that their centers all end up in ?
Hannah Alpert (Department of Mathematics and Statistics, Auburn University, USA)
Solution by the proposer
Yes. We think of tiles as being specified by their centers, so we use the word “tile” to mean “center of a tile” whenever the meaning is unambiguous. Our first lemma shows that it suffices to slide the tiles to , which we define to be the lattice that contains as well as all the vertices of the hexagons of the original tiling. This lattice is generated by the vectors and , which are orthogonal to and , respectively.
Lemma 1. Starting with any arrangement where all tiles are in , we can slide so that they all end up in .
Proof. We use induction on the number of tiles not in . Among the tiles not in , find those with the least -coordinate, and among these, select the one with the least -coordinate. Either this tile can slide down along to a point in , or it can slide down-left along to a point in . ∎
We want to slide from an arbitrary tile arrangement to . In the starting arrangement, sliding is obstructed by tangencies, which are pairs of tiles that touch. When two tiles touch only at vertices, we call it a double tangency. We can make a graph of all tangencies by drawing an edge between the centers of each pair of tiles that are tangent, whether they are both unglued tiles, or one unglued and one glued, or both glued; this graph is embedded in the plane. Any subset of the tangencies determines a linear subspace of , consisting of the infinitesimal perturbations of the unglued tiles that preserve those tangencies. If a pair of tiles is tangent but the tangency is not included in the subset, the perturbation is allowed to destroy the tangency, either by making the tiles overlap, or by creating a gap between them. We say that a tangency graph is rigid if this linear subspace of perturbations is trivial.
Our strategy for sliding all tiles to is to find a perturbation direction that preserves all the tangencies, and slide in that direction until a new tangency forms. Then we find a perturbation direction that preserves all the tangencies, including the new one, slide in that direction, and so on, until the graph of all tangencies becomes rigid. The next lemma completes the proof.
Lemma 2. If the graph of all tangencies of an arrangement of tiles is rigid, then all tiles are in .
Proof. First we describe in more detail how a tangency graph determines a linear subspace of perturbations. For some tangencies, the vector along that edge of the graph is fixed: this includes any tangency between two glued tiles, and any double tangency. Otherwise, the edge vector is determined by a variable offset. There are three types of tangencies with variable offsets, corresponding to the three directions of tile sides along which the tangency may occur. The linear subspace of perturbations is specified by a system of linear equations, with one variable for each variable offset, and two equations for each face of the tangency graph, which mandate that the sum of vectors along the edges of that face is zero as a vector in .
To prove the lemma, we consider subgraphs of the graph of all tangencies; these subgraphs contain all the tiles and all the edges with fixed edge vectors, but not necessarily all the edges with variable offset. We show by induction on the number of edges with variable offset that if a tangency subgraph is rigid, then all of its edge vectors are in . This implies that the tiles are also in , because in a rigid tangency subgraph, every unglued tile has a path connecting it to a glued tile.
Consider the case where a face has only one edge with variable offset. Then that edge vector is determined by the others along that face, so if we remove that edge, the resulting tangency subgraph is still rigid, and we may apply the inductive hypothesis.
Next, consider the case where a face has (at least) two edges with variable offsets, of different types. The sum of these two edge vectors uniquely determines their two offsets, so the two edge vectors are determined by the others along that face. Thus, removing both edges gives a rigid tangency graph, to which we can apply the inductive hypothesis. The fact that the sum of the two edge vectors is in implies that each of the two is in .
To address any remaining cases, we draw the dual graph to the tangency subgraph, with one vertex for each face of the tangency subgraph, and one edge for each edge with variable offset in the tangency subgraph, connecting the faces on the two sides of that edge. If the dual graph has no loops or cycles, then either it has no edges, so we are in the base case, or it has a vertex with only one edge, so we are in the first case already addressed. If the dual graph has a cycle with edges of more than one type, then we are in the second case already addressed. The remaining case is where the dual graph has a loop or cycle with edges of only one type, but this contradicts rigidity, because we could shift all tiles enclosed by the cycle. Thus, there are no remaining cases. ∎
277
Find two non-homeomorphic topological spaces and such that their products with the interval, and , are homeomorphic.
Guillem Cazassus (Mathematical Institute, University of Oxford, UK)
Solution by the proposer
One can take the 2-sphere with 3 discs removed, and the 2-torus with one disc removed. These can both be seen as obtained from the 2-disc by attaching two 1-handles, as in Figure 1. After taking their products with , the extra dimension added allows to exchange the attaching positions of the handles to go from the first picture to the second.
278
What is the topology of the space of straight lines in the plane?
Guillem Cazassus (Mathematical Institute, University of Oxford, UK)
Solution by the proposer
Call this space . It is an open Möbius strip: here are two possible ways to see this.
Solution 1:
Let correspond to the lines passing through the origin. Then is a circle , and one can consider the projection sending a line to its parallel passing through 0. This is a fibration, with fiber , and the inclusion gives a section of it. There are two such fibrations possible: the trivial one (cylinder) and the Möbius strip. The one we consider cannot be trivial, otherwise it would mean that one can find another section disjoint from . This would mean that one can take a given line disjoint from the origin, and half-twist it continuously without hitting the origin. Therefore, it is the Möbius strip.
Solution 2:
We can view as the quotient of , the space of oriented lines. First, can be identified with the cylinder , the first coordinate being the angle with the horizontal axis, and the second the “algebraic distance” to the origin (take the distance, and put a minus sign if the origin is at the left of the line).
Second, under this identification, the involution reversing the orientation of a line is the map , and . It follows that can be obtained from the strip (a fundamental domain for ) by identifying its two edges by the twist , which gives a Möbius strip.∎
279
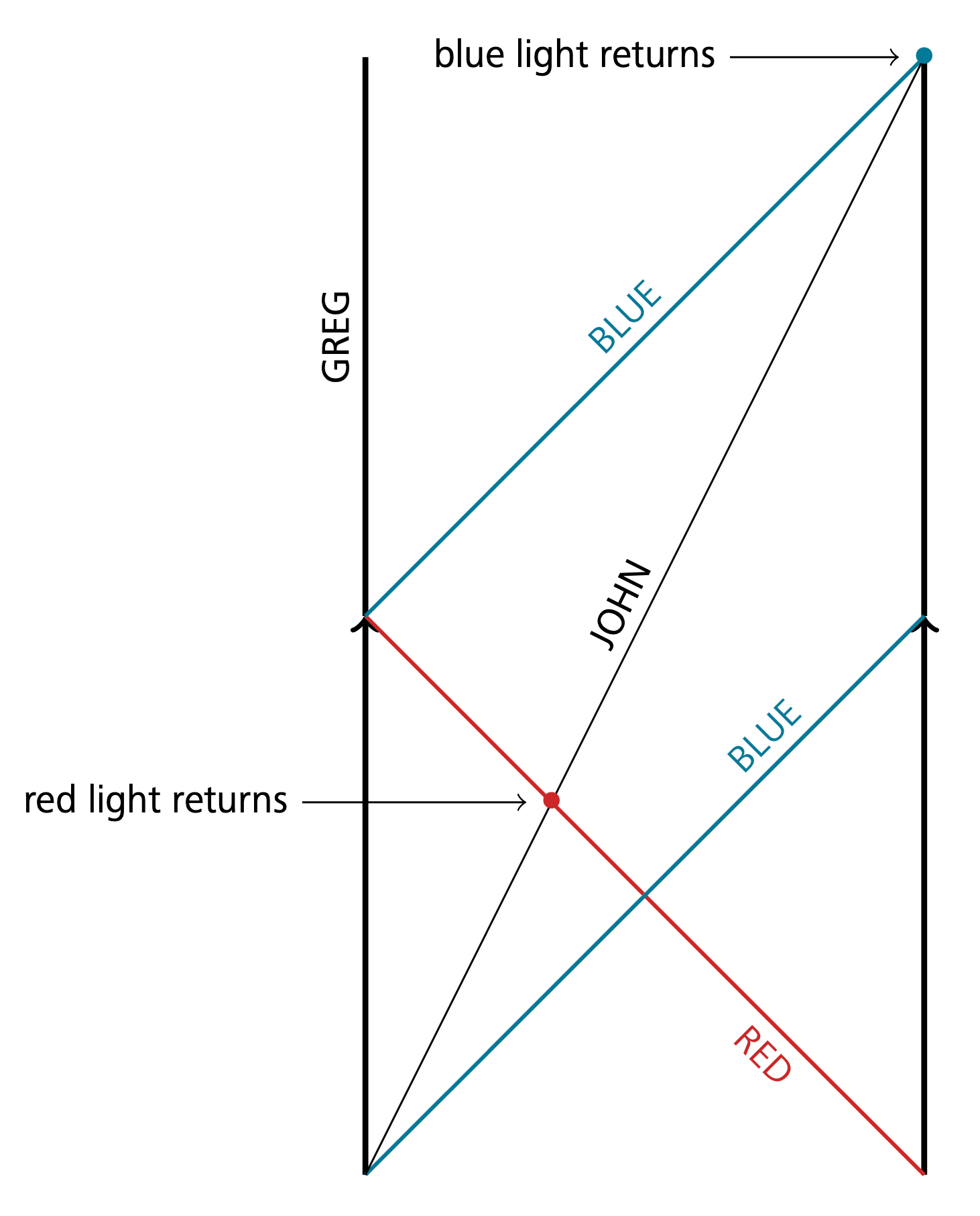
In the standard twin paradox, Greg stays at home whilst John travels across space. John finds, upon returning, that he has aged less than Greg. This is an apparent paradox because of the symmetry in the situation: in John’s rest frame, it seems like Greg is doing the moving and so should also be experiencing time dilation. The standard explanation of the paradox is that there is no symmetry: at some point John needs to turn around (accelerate), so, unlike Greg, John’s rest frame is not inertial for all times. So let’s modify the set-up: suppose that space-time is a cylinder (space is a circle). Now, John eventually comes back to where he started without needing to decelerate or accelerate. In this fleeting moment of return, as the twins pass one another, who has aged more?
Jonny Evans (Department of Mathematics and Statistics, University of Lancaster, UK)
Solution by the proposer
John has aged more. You can just integrate to compute his proper time and see it is smaller. If the speed of John is , the size of the universe is and the speed of light is , then the proper time until return measured by John is
against Greg’s .
But why is this not a paradox? Again, the problem is that, despite appearances, there is no symmetry in the situation. In other words, there is no global isometry of space-times interchanging their rest frames. Space-time is foliated by a distinguished family of closed space-like geodesic loops. These are orthogonal to Greg’s world-line, but not to John’s. This means that, unlike in Minkowski space-time, John could do an experiment to figure out that he is moving. For example, suppose that Greg sees John moving to the right. If John emits a red light ray leftwards and a blue light ray rightwards, and waits for them to circle around the universe, he will see the red light ray return first; see Figure 2.∎
You can read a more leisurely discussion of this version of the twin paradox in the following paper: J. R. Weeks, The twin paradox in a closed universe. Amer. Math. Monthly108, 585–590 (2001).
280
The -dilation of a piecewise smooth map is the degree to which it stretches -dimensional area. Formally, for a map between subsets and , or more generally between Riemannian manifolds,
where is the induced map on the -th exterior power and is the operator norm. A map of rank has -dilation zero, so this can be thought of as a quantitative refinement of rank.
Consider the rectangular prism .
Let be a map of relative degree, that is, it restricts to a degree- map between the boundaries of the rectangles. Show that the -dilation of such a map is bounded below by a which does not depend on .
Now let be the minimum -dilation of a surjective map . Construct examples to show that as .
Fedor (Fedya) Manin (Department of Mathematics, University of California, Santa Barbara, USA)
Solution by the proposer
The statement follows from applying the idea that “-dilation is the degree to which the map stretches area of surfaces” to the boundary. Let be a map of relative degree , and write for the area form on . By the definition of degree,
Now, , and therefore
Therefore, .
Assume that for some integer . We will construct a map with . The basic idea is to use the fact that has much larger volume than . Some portion of that volume will be cut up into chunks, shrunk down by a factor of around , and distributed surjectively over . The rest will be used to make the map continuous; this may be highly distorted, but does not contribute to the -dilation because it maps to a one-dimensional subspace of .
Split into an grid of cubes of side length . These are in one-to-one correspondence with an grid of cubes in of side length . Let be the cube of side length which is concentric with . We define on each so that it maps to the center of and the interior of surjectively over , with . Such a map can be made -Lipschitz, and therefore its -dilation is . Outside the , we can extend this map to a smooth map whose image is a tree embedded in , the vertices of which are the centers of the . Since the tree is one-dimensional, the -dilation of this portion is zero.
This problem demonstrates a tension frequently encountered in metric geometry. Suppose you are trying to construct a map between two spaces with certain properties and geometric bounds. When you try to do it the obvious way, the geometric complexity blows up in one direction but stays very small in another. Can the map be modified by “trading off” these dimensions while preserving the desired properties?
Both halves of the problem are inspired by research papers: (2) is an approximate version of a construction by Kaufman of a rank map from the cube to the square [7 R. Kaufman, A singular map of a cube onto a square. J. Differential Geometry 14, 593–594 (1979) ], while (1) is a simple case of a complex and surprising result of Guth [6 L. Guth, The width-volume inequality. Geom. Funct. Anal. 17, 1139–1179 (2007) , Theorem 2]. For other pairs of rectangles Guth shows, using a very different construction, that one can trade off between different dimensions to some degree even while constructing maps of relative degree . Both Kaufman’s and Guth’s constructions have inspired further work. For instance, Wenger and Young [8 S. Wenger and R. Young, Lipschitz homotopy groups of the Heisenberg groups. Geom. Funct. Anal. 24, 387–402 (2014) ] used a construction similar to Kaufman’s to show that certain Lipschitz maps from spheres to Heisenberg groups (unexpectedly!) have Lipschitz extensions to balls. In contrast, Goldstein, Hajłasz and Pankka [5 P. Goldstein, P. Hajłasz and P. Pankka, Topologically nontrivial counterexamples to Sard’s theorem. Int. Math. Res. Not. IMRN, no. 20, 7073–7096 (2020) ] used a Kaufman-style construction to create low-rank maps which are actually topologically nontrivial.
281
Given a triangle in the (real or complex) plane, show that there is a natural bijection between the set of smooth conics passing through the vertices and the set of lines avoiding the vertices.
Jack Smith (St John’s College, University of Cambridge, UK)
Proof by the proposer
Suppose is a conic through the vertices , , and of the triangle, and let , , and be its respective tangent lines at these points. By Pascal’s theorem, the intersections , , and are collinear, lying on a line say. We claim that the map (is well defined and) gives the desired bijection.
To prove this, take homogeneous coordinates on the plane in which , , and are , , and , respectively.
A general conic through these points is described by the equation
for a unique in . The conic is smooth if and only if , , and are all non-zero. Meanwhile, a general line in the plane is described by the equation
and it avoids , , and if and only if , , and are all non-zero. It therefore remains to show that the map induces a bijection from triples of non-zero scalars to triples of non-zero scalars .
Suppose then that is the smooth conic
Differentiating, we see that the line is , so
Similarly and , and we see that there is a unique line through these points, with the equation
So the map is well defined and corresponds to
This is a bijection, with inverse
so we are done. ∎
We wait to receive your solutions to the proposed problems and ideas on the open problems. Send your solutions to Michael Th. Rassias by email to mthrassias@yahoo.com.
We also solicit your new problems with their solutions for the next “Solved and unsolved problems” column, which will be devoted to discrete mathematics.
References
- A. Edelman, E. Kostlan and M. Shub, How many eigenvalues of a random matrix are real? J. Amer. Math. Soc. 7, 247–267 (1994)
- T. Tao and V. Vu, From the Littlewood–Offord problem to the circular law: universality of the spectral distribution of random matrices. Bull. Amer. Math. Soc. (N.S.) 46, 377–396 (2009)
- T. Tao and V. Vu, Random matrices: Universality of local spectral statistics of non-Hermitian matrices. Ann. Probab. 43, 782–874 (2015)
- V. H. Vu, Recent progress in combinatorial random matrix theory. Probab. Surv. 18, 179–200 (2021)
- P. Goldstein, P. Hajłasz and P. Pankka, Topologically nontrivial counterexamples to Sard’s theorem. Int. Math. Res. Not. IMRN, no. 20, 7073–7096 (2020)
- L. Guth, The width-volume inequality. Geom. Funct. Anal. 17, 1139–1179 (2007)
- R. Kaufman, A singular map of a cube onto a square. J. Differential Geometry 14, 593–594 (1979)
- S. Wenger and R. Young, Lipschitz homotopy groups of the Heisenberg groups. Geom. Funct. Anal. 24, 387–402 (2014)
Cite this article
Michael Th. Rassias, Solved and unsolved problems. Eur. Math. Soc. Mag. 131 (2024), pp. 59–64
DOI 10.4171/MAG/176