This article presents some results obtained recently in the history of mathematics using the tools of textometry. The results pertain to two case-studies, devoted to Charles Hermite’s style and to the theory of algebraic surfaces at the end of the 19th century, respectively.
It goes without saying that words of natural language have many essential roles in a published mathematical text. They give a title to this text and divide it into sections. They express acknowledgements to people and institutions. They make possible the reference to other texts. They signal the statement of a result and the beginning of its proof. They organise and articulate sequences of computations. Associated with mathematical symbols, diagrams and figures, of which they help fixing the meaning, they allow to express theorems, proofs, motivations, heuristic explanations.
Taking into consideration words of natural language is thus unavoidable if one wishes to understand a given text, be it in a mathematical or a historical perspective. In the latter case, looking at the references and the acknowledgements helps situating a mathematician of the past into various collective frames. Analysing this mathematician’s technique may be a way to uncover and grasp phenomena at work at larger scales, such as disciplinary reconfigurations between, say, geometry and algebra. Reading introductions of papers often allows a better appreciation of his or her viewpoint on a topic. And focussing on isolated technical words may also be fruitful, inasmuch as their very use can be the trace of specific traditions: for instance, in the late 19th century, what we call nowadays the genus of algebraic curves was named Geschlecht, genre, genere by German, French and Italian mathematicians, but deficiency by the British, and this asymmetry was rooted in different original conceptions of the notion [7 F. Lê, “Are the genre and the Geschlecht one and the same number?” An inquiry into Alfred Clebsch’s Geschlecht. Historia Math. 53, 71–107 (2020) ].
Investigating specific parts of a text, even reduced to a single word, may thus lead to interesting historical results. But what happens if one tries to deal with the set of all the words that compose a text or a group of texts?
During the past decades, researchers in the history of literature have developed and used computer-aided statistical techniques aimed at handling the whole word mass of large corpora, which allowed them to detect phenomena that were hard to capture with the naked eye: semantic and syntactic peculiarities of authors, assessment of lexical richness, detection of privileged associations between groups of words, thematic classification of texts, etc. Such an approach to textual corpora, where one relies on quantitative computations all the while looking closely at the texts to draw solid conclusions, comes under what is called “textometry,” “lexicometry” or “statistical analysis of textual data.”1See for instance [10 L. Lebart, B. Pincemin and C. Poudat, Analyse des données textuelles. Mesure et évaluation 11, Presses de l’Université du Québec (2019) ] for an overview on the topic.
A few years ago, my curiosity led me to try applying the methods of textometry to gain a new view on corpora of old mathematical texts. My hope was that this would be a way to find new (kinds of) results in the history of mathematics or, at least, to confirm intuitions that had been formulated by myself or by others before. In what follows, I present a sample of the results that have been obtained so far. They pertain to two independent situations: the mathematician Charles Hermite on one hand, and the theory of algebraic surfaces in the journal Mathematische Annalen between 1869 and 1898 on the other hand.
Before delving into these case-studies, let me briefly make some remarks on the general functioning of the chosen textometry software and on the associated terminology.
1 Counting words
The software that has been selected for my investigations is the open-source one TXM [5 S. Heiden, The TXM platform: Building open-source textual analysis software compatible with the TEI encoding scheme. In Proceedings of the 24th Pacific Asia Conference on Language, Information and Computation, pp. 389–398, Institute for Digital Enhancement of Cognitive Development, Waseda University, Tokyo, Japan (2010) ]. Given a corpus of texts formatted in an appropriate manner, this software begins by listing all the words that constitute these texts. It also attaches to each word a lemma, that is, the entry that would correspond to this word in a dictionary, as well as a grammatical label that indicates the part of speech corresponding to the word. For instance, the word “Theorems” would be associated with the lemma “theorem” and the grammatical label “common noun.”
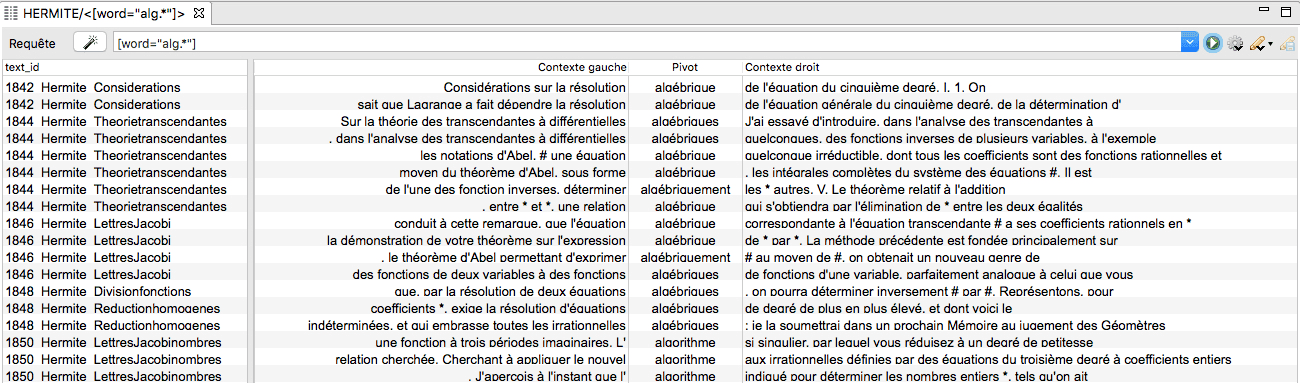
The corpus can then be interrogated according to various requests, the results of which are typically displayed as lists: list of the most frequent lemmas, list of the words containing a given chain of characters, list of verbs to the present indicative, etc. It is also possible to get the lists of given words together with their close textual neighbourhoods, and to sort them according to several criteria (see Figure 1). A non-trivial issue for the researcher is then to determine which lists will be significant for a given historical purpose, and to make sense of them. The same remark holds for the other, more complex functions that are provided by the software TXM; I will explain their basic principles when I display their utility in my case-studies.
Before that, the problem of the mathematical formulas must be raised. For some technical and methodological reasons I have not succeeded yet to take formulas into account satisfactorily in the quantitative treatment. Hence a radical operation of razing these formulas has been done (manually) during the initial text formatting: each in-line formula has been replaced by a symbol , and each displayed formula has been replaced by a symbol #. This operation thus only allows to keep track of the number of formulas in the statistical counts. That said, since the quantitative results must always be supported by a reading of the original texts, the content of the formulas is taken into account in the interpretative phase. Moreover, as will be seen, it turns out that the mere counting of the symbols and # provides some information on the texts.
Another comment must be made on the technical terminology coming from textometry. Without entering into details, a word can be a word of natural language, a punctuation mark, a number written with digits or any symbol such as § or . The frequency of a word in a corpus designates its absolute number of occurrences. A word of frequency is called a hapax. Consider for instance the sentence within the quotation marks: “The continuous function is a uniformly continuous function.” It contains 10 words,2Do not forget the period! distributed into 6 hapaxes and 2 words of frequency 2.
Finally, one is often lead to compare several corpuses (or several parts of one corpus). A question, then, is to ascertain if some words are over- or under-represented in one corpus or the other, considering their size difference – the main difficulty is that making a linear adjustment of the numbers is not satisfactory enough because it does not take into account the actual word distribution in the corpus.3See [10 L. Lebart, B. Pincemin and C. Poudat, Analyse des données textuelles. Mesure et évaluation 11, Presses de l’Université du Québec (2019) , pp. 122–123] and the reference to Pierre Lafon’s works given there. Based on computations associated with a hypergeometric model of word distribution, the notion of specificity allows to answer this question nicely, through the calculation of a specificity score. In the case of two corpuses, the over- (resp., under-) representation of a word corresponds to a positive (resp., negative) specificity score; the higher the latter, the stronger the over-representation.
2 Charles Hermite’s style
Celebrated by his contemporaries as one of the most influential mathematicians of the 19th century, Charles Hermite (1822–1901) is still renowned nowadays for various mathematical achievements. Beyond the objects and theorems named after him, his 1873 proof of the transcendence of is probably the most emblematic result that we owe to him. The year 2022 has marked the bicentenary of his birth, and has caused a number of new historical research projects on him.4A forthcoming special issue of Revue d’histoire des mathématiques is devoted to this bicentenary. It will include the paper [9 F. Lê, On Charles Hermite’s style. Rev. Histoire Math., to appear ], which corresponds to the present section. More generally, for a rich and deep study of numerous aspects of Hermite’s work, see the publications of Catherine Goldstein, such as [3 C. Goldstein, The Hermitian form of reading the disquisitiones. In The shaping of arithmetic after C. F. Gauss’s Disquisitiones arithmeticae, pp. 377–410, Springer, Berlin (2007) , 4 C. Goldstein, Charles Hermite’s stroll through the Galois fields. Rev. Histoire Math. 17, 211–270 (2011) ].
The question about Hermite that interested me was to describe his style, that is, to account for the impression that one gets when reading his mathematical writings. More precisely, while concentrating on his mathematical publications, the aim was to focus on the literary side of his writing, and not on what could be called his mathematical style. In other words, the idea was to ignore the facets of his works related to how given mathematical domains and objects intervened in his proofs, or how epistemic values shaped his practice, for instance. Instead, I wanted to bring to light the mechanisms through which his texts acquire a particular literary taste.
In fact, other historians had already hinted at such a question. In a booklet devoted to several works on irrationality and transcendence, Michel Serfati wrote:
In the middle of the 18th century, Lambert […] clearly exposes his mathematical intuitions […] and resorts quite frequently to what could be called light metaphors and to active verbal forms, which are the grammatical consequences of an explicit “I.” […] Thirty years later, Legendre makes passive forms predominant, forms which are characteristic of the contemporary style […]. In Hermite, a man with a modest personality, it is almost the modern style, synthetic, neutral in form and content, characteristic of the modern exclusion of the author in the mathematical text. [13 M. Serfati, Quadrature du cercle, fractions continues et autres contes : Sur l’histoire des nombres irrationnels et transcendants aux XVIIIe et XIXe siècles. Brochure A.P.M.E.P. 86 (1992) ]
Quite surprisingly, an opposite image of Hermite’s style appears in a paper of Catherine Goldstein, in a passage where she comments on the possible youthful sources of Hermite:
More difficult to pinpoint, but quite characteristic, the flavour of Hermite’s mathematical prose itself reminds the reader strongly of these French authors [Lagrange, Legendre, Cauchy, Fourier]. The style is discursive and oriented towards the description of processes. [3 C. Goldstein, The Hermitian form of reading the disquisitiones. In The shaping of arithmetic after C. F. Gauss’s Disquisitiones arithmeticae, pp. 377–410, Springer, Berlin (2007) ]
As will be shown, my analysis tended to confirm (and enrich) Goldstein’s assertions rather than Serfati’s.5It must be emphasised, though, that the two historians were looking at two distinct pieces of Hermite’s publications, which possibly led to different appreciations. My own approach considers at once almost all the published articles of Hermite.
In any case, the stylistic features evoked in these quotations are exactly of the kind that interested me, and that I wanted to quantify precisely using the tools of textometry. The following lines thus aim at showing that Hermite can be seen as a mathematical narrator whose presence in the written texts is made explicit through various markers, such as the use of the first person singular associated with verbs that describe the mathematical action in a lively way, and with the lexical field of the personal views.
Left portrait: Mathematishe Gesellschaft in Hamburg / source: Archives of the Mathematisches Forschungsinstitut Oberwolfach / CC BY SA 2.0 DE / Right Portait: CC0-1.0
To do so, the approach will be comparative. Indeed, and as it is apparent in the previous quotations, the assessment of the particularities of an author is always done (even if implicitly) with regards to a certain point of reference, consituted by another author or by more general norms of writings. In Hermite’s case, I decided to confront him with Camille Jordan (1838–1922), a French mathematician separated from Hermite by about one generation, and who shared with him a number of research topics.
Since the objective is to investigate Hermite’s prose in his mathematical publications, our corpus of reference is made of his research papers written in French, as they appear in his Œuvres complètes. This represents 186 papers published between 1842 and 1901, and a total of 364,412 words. Jordan’s corpus is made in the exact same way and gathers 122 articles published between 1861 and 1920. Although it contains less texts than Hermite’s corpus, it has more words, with a total of 591,732 words (see Table 1).
| Texts | Words | Hapaxes | |
| Hermite | 186 | 334,001 | 2,045 |
| Jordan | 122 | 529,766 | 2,014 |
2.1 The personal comments
One possibility to enter into this mass of words is to examine the hapaxes. These particular words are, indeed, a usual way to grasp the side of an author’s style related to the notion of lexical richness: the more hapaxes a corpus contains, the richer it is. From such a numerical point of view, with 2,045 hapaxes for Hermite against 2,014 for Jordan, the former’s corpus appears as lexically richer as the latter’s, especially given the size difference between them. However, it is first and foremost on the semantic content of the hapaxes that I would like to expand here.6The numerical side of the problem is linked to the question of lexical diversity. This question is investigated in [9 F. Lê, On Charles Hermite’s style. Rev. Histoire Math., to appear ], together with that of lexical sophistication.
Let me first recall that, generally speaking, hapaxes fill up to 30%–45% of the number of distinct words of a (French) literary text, depending on the genre and the author, which might seem very high at first sight. In Hermite’s case, the hapaxes represent about 32% of the distinct words. Many of them are completely usual words, as is exemplified by the hapaxes essai (“attempt”), rencontrés (“met,” in a masculine plural form) and Comparaison (“Comparison”).7Because of the capital C, Comparaison is not the same as comparaison from the viewpoint of word counting, even though the two words have the same lemma. Other hapaxes are technical terms whose unique use reflects marginal mathematical questions within Hermite’s works, like in the case of quadrique.8Throughout this paper, all the French and German terms that are not translated are supposed to have a transparent meaning in English. A perfectly analogous phenomenon is to be seen in Jordan, for whom torrents and cirques are hapaxes involved in a paper related to questions of mountainous geography.
The other hapaxes reveal two important differences between our authors. The first one is linked to a structural feature of the Hermitian corpus: 70 of its 186 papers are extracts of letters that have been published in research journals at Hermite’s time. On the contrary, there exists only one such paper in Jordan’s corpus.
Now, a large part of the Hermitian hapaxes is clearly due to this epistolary format. They refer in particular to many variations on the theme of the delay of answer, the associated excuses, the acknowledgements and the sociable chat. Thus, in a letter written to Carl Gustav Jacob Jacobi in 1847 (and published in an 1850 issue of Journal für die reine und angewandte Mathematik), Hermite wrote:
Près de deux années se sont écoulées, sans que j’aie encore répondu à la lettre pleine de bonté que vous m’avez fait l’honneur de m’écrire. Aujourd’hui je viens vous supplier de me pardonner ma longue négligence et vous exprimer toute la joie que j’ai ressentie en me voyant une place dans le recueil de vos Œuvres. Depuis longtemps éloigné du travail, j’ai été bien touché d’un tel témoignage de votre bienveillance; permettez-moi, Monsieur, de croire qu’elle ne m’abandonnera pas […].9“Almost two years have passed, and I have not yet responded to the letter, filled with kindness, that you made me the honor to write to myself. I am coming today to beg you to forgive my long negligence, and to express all the joy that I have felt by seeing for myself some room in the collection of your works. Having been away from work for a long time, I have been very touched by such a testimony of your benevolence. Allow me, Sir, to believe that it will not abandon me […].” The French words in italics are the hapaxes.
All these hapaxes, which clearly colour Hermite’s texts in a characteristic way, have almost no counterpart on Jordan’s side because of the quasi non-existence of published letters.
Nevertheless, the texts written by Hermite which are not extracts of letters are also rich in hapaxes. Many of these words have a meliorative function, and are used in passages where Hermite comments on diverse mathematical questions, objects, theorems or works. Examples of such hapaxes include mystère, paradoxe, prestige, lumière (“light”), guide, inattendu (“unexpected”), magnifiques, stérile, …, or those of the following quotation, where Hermite talks about a certain formula that had been earlier worked on by Leopold Kronecker:
M. Kronecker, en la donnant comme l’expression analytique d’un de ses théorèmes, avait bien évidemment pressenti la signification qu’elle recevrait dans la théorie des fonctions elliptiques, et, à cet égard, je ne puis trop admirer la pénétration dont il a fait preuve.10“Mr. Kronecker, by giving it as the analytic expression of one of his theorems, had obviously foreseen the meaning that it would receive in the theory of elliptic functions, and, in this respect, I cannot but admire the insight he demonstrated.”
Such comments are much scarcer in Jordan’s corpus. In fact, most of the hapaxes which are about the expression of personal viewpoints refer to a specific episode, namely a scientific quarrel with Kronecker that occurred in 1874 [1 F. Brechenmacher, La controverse de 1874 entre Camille Jordan et Leopold Kronecker. Rev. Histoire Math. 13, 187–257 (2007) ]. The hapaxes contradicteur (“detractor”), excusable, objective, incontestable (“indisputable”), jugé (“judged”), complaisance (“complacency”), … occur in the related publications.
From this point of view, the Hermitian prose appears as more personal than the Jordanian one. By writing to his colleagues and his friends, and by abounding with various personal comments on many issues, Hermite appears very explicitly within his mathematical texts.
Such a picture can also be drawn from the inspection of the common nouns, the adjectives and the adverbs that are specific to Hermite. For instance, méthode, recherche, facile (“easy”), important, beau (“beautiful”) and essentiel are terms which are abnormally more used by Hermite; they clearly display the semantic field of the expression of the personal viewpoints on diverse aspects of the mathematical work. In this case, too, there are no equivalents of such words in Jordan’s work, who thus appears as being more neutral, or less directly committed in his publications.11The examination of the terms that are specific to Jordan is interesting because many of them are related to the proof by contradiction, with hypothèse, absurde, inadmissible, contraire, and the French adverbs of negation ne, pas. A systematic counting of this kind of reasoning shows that it is used 599 times by Jordan, and only 35 times by Hermite…. This curious feature, however, is not related to the question of style as I wished to understand.
2.2 The mathematical action
To describe how Hermite conducts the mathematical narration, the grammatical categories of the verbs and the personal pronouns are now considered.
First of all, it is telling to look at the list of the verbs which are the most specific to Hermite: ai, savoir, conduit, tire, faisant, donne, supposant, vais, conclut, trouve, obtient, obtenir, écrire, observe, a, été, remarque, employant, parvenir, trouvera. For Jordan, the most specific verbs are: sera, contient, formé, contiendra, pourra, contenu, aura, Soient, contenant, déplace, Supposons, forme, être, existe, serait, déplacent, seront, transforme, succéder.
From the semantic point of view, Jordan’s list contain a few technical verbs (such as contient, contiendra, contenu, contenant, which are inflections of the infinitive contenir: “to contain”) as well as a certain number of stative verbs (such as sera, serait, seront, which come from the infinitive être: “to be”). On the contrary, one finds on Hermite’s side a variety of verbs which evoke the description of processes, with the inflections of conduire, tirer, trouver, observer, écrire (“to lead,” “to draw,” “to find,” “to observe,” “to write”) among others.
Furthermore, as the conjugated forms of these verbs let us guess, the grammatical subjects that are associated with them are not of the same kind: for Jordan, these subjects are very often the mathematical objects themselves – for instance, it is a group that “contains” an element – while the action described by Hermite’s verbs is taken care of by a person, real or fictive – it is someone who “draws” a conclusion from a premise.
This asymmetry is confirmed by the inspection of the personal pronouns. Those that are over-represented in Hermite’s corpus are related to the different forms of the first person singular je (“I”), the semi-impersonal on (“one”) and the second person plural. The latter is due to the French vouvoiement, which appears exclusively in the published letters. It is however remarkable that the over-abundance of the je and the on holds even after removing these special publications from the comparative counting. Jordan, on his side, favours the employment of the personal pronouns related to il and elle (“he/it,” “she”). The il, for instance, almost never refers to a person; its occurrences either designate mathematical objects or are used in impersonal, fixed phrases such as il y a, il faut, il existe (“there is,” “one has to,” “there exist(s)”).
These are the differences that can be observed within the set of all personal pronouns. Considering now the overall numerical distribution of grammatical categories in each corpus, it turns out that Hermite’s texts contain significantly more such pronouns than Jordan’s ones. This echoes the fact that many verbs used by Hermite cannot have a mathematical object as their subject, and are often associated with the je or the on. On the contrary, in Jordan, many sentences have a mathematical object as their subject, even if this object is referred to by a single letter, as in: “Thus, contains substitutions.” This kind of writing thus tends to diminish the number of personal pronouns used by Jordan.
Finally, the two lists of verbs given at the beginning of this subsection reflect the existence of an imbalance between the modes and the tenses in which the verbs are conjugated. Indeed, as is disclosed by a computation of the specificity scores of these modes and tenses, the simple future is clearly over-represented in Jordan’s writings, while the present indicative, the infinitives and the participles proliferate on Hermite’s side.12Jordan’s corpus is also abnormally rich in conditional, subjunctive and, to a lesser extent, imperfect indicative. This imbalance is to be linked to the over-use of proofs by contradiction that we alluded to above.
The case of the future is particularly interesting. To a great extent, the simple futures used by Jordan are associated with the expression of mathematical facts, as in: Ce système ne contiendra donc en général qu’une fraction des substitutions du système primitif.13“In general, this system will thus contain only a fraction of the substitutions of the primitive system.” The future is also used by Hermite, but in a different way: the preference goes to combinations of a conjugated form of aller (“to go”) and an infinitive: Cette remarque faite, je vais étudier de plus près les quotients ….14“This remark being made, I am going to study closer the quotients ….” These two expressions of the (grammatical) future do not have exactly the same meanings and colours. In particular, the one used mostly by Hermite contributes to animate the mathematical narration with a kind of immediacy in the description of processes.
To finish this discussion on the verbs, let me remark that it is quite characteristic that Supposons (“Let us suppose”) is specific to Jordan, whereas supposant (“supposing”) is on Hermite’s side: both verbs have obviously the same meaning, but the way they are conjugated implies different turns of phrases and different writing flavours.
Although other grammatical categories, such as the conjunctions or the demonstrative adjectives, could complete this picture, I will not elaborate on them for reasons of space. Still, it is quite amusing to take a look at the list of the beginnings of sentences (made of two words) which are specific to one author or the other (see Table 2). One finds in it several characteristics that echo what has been explained above: on Hermite’s side, the involvement of the first person singular, the use of verbs of action, but also the employment of adverbs and other phrases which are yet other testimonies of the liveliness of his prose: Cela étant, De là, Voici maintenant (“This being said,” “From this,” “Here is now”), etc. More impersonal formulations are to be found in Jordan’s list, many elements of which also point to sentences with mathematical objects as their subject.
| Sentence beginning | Freq. H. | Freq. J. | Spec. score |
| Cela étant | 195 | 3 | 93.5 |
| C’est | 234 | 55 | 68.0 |
| bstrutOr, | 283 | 36 | 61.0 |
| De là | 80 | 8 | 31.0 |
| Je me | 52 | 4 | 21.4 |
| J’observe | 39 | 0 | 19.7 |
| Effectivement, | 43 | 42 | 19.1 |
| Je remarque | 39 | 1 | 18.3 |
| J’ai | 53 | 12 | 16.1 |
| Ainsi, | 62 | 20 | 15.8 |
| On trouve | 40 | 5 | 14.9 |
| Maintenant, | 32 | 1 | 14.8 |
| Voici maintenant | 29 | 0 | 14.7 |
| D’autre | 3 | 180 | -24.9 |
| Soit | 68 | 512 | -28.1 |
| Soient | 42 | 409 | -29.4 |
| En effet | 74 | 547 | -29.4 |
| D’ailleurs | 29 | 385 | -33.0 |
| Les substitutions | 5 | 285 | -38.9 |
| On aura | 33 | 533 | -50.4 |
| Le groupe | 2 | 332 | -50.6 |
| Donc | 4 | 417 | -61.2 |
| Si | 11 | 813 | -115.2 |
As the absolute numbers in Table 2 recall, everything that has been stated about the specificities has to be first and foremost interpreted as relative results. In particular, there is no question of asserting that Hermite never uses the simple future, or that he never writes sentences of which the subject is a mathematical object, etc. The specificities tell us that some features are significantly not equally distributed within the two corpuses.
2.3 Hermite, Jordan … and the others?
A natural question that arises, now, is to determine whether the characteristics of Hermite’s style that have been sketched in this section only appeared because the opposite figure was Jordan. Among others, the relative depersonalisation of Jordan’s prose might be linked to the fact that he was born 16 years after Hermite. Hence it would be illuminating to confront Hermite with a mathematician who would have been educated and who wrote papers roughly during the same period as Hermite did.
Ideally, this new mathematician should also have devoted approximately the same number of works to the same mathematical domains as Hermite did. Indeed, as my second case-study shows, mathematical domains are not indifferent to the matters of specificities of words and grammatical categories.
3 The theory of algebraic surfaces
Turning now to the theory of algebraic surfaces, the corpus of reference is made of all the papers dealing with this subject, written in German and published in Mathematische Annalen between 1869 and 1898.15The results of the present section come from [8 F. Lê, Le théorie des surfaces algébriques dans les Mathematische Annalen à l’épreuve de la textométrie (1869–1898). Rev. Histoire Math. 28, 1–45 (2022) ]. This represents 75 papers and 632,926 words. A notable difference with the Hermite–Jordan case is that the corpus is a collective one: 26 authors are to be counted, the most prolific of whom are Alfred Clebsch (1833–1872) and Rudolf Sturm (1841–1919), with 6 and 7 papers, respectively.
When tackling this corpus on algebraic surfaces, the issue was not to deal with the notion of style. My intention was to see what original information on the corpus could be brought by textometric techniques, by investigating the words of natural language, the punctuation marks and the symbols and # standing for mathematical formulas.
To get a first view on the corpus, let us consider the common nouns and the proper nouns that appear the most (see Table 3).
| Common nouns | Freq. | Proper nouns | Freq. |
| Fläche | 8,041 | Clebsch | 114 |
| Punkt | 7,876 | Cayley | 66 |
| Kurve | 4,934 | Cremona | 60 |
| Ordnung | 4,698 | Salmon | 57 |
| Gerade | 4,458 | Zeuthen | 45 |
| Ebene | 4,020 | Schläfli | 49 |
| Gleichung | 2,544 | Sturm | 41 |
| Knotenpunkt | 1,398 | Fiedler | 41 |
| Kegel | 1,308 | Crelle | 36 |
| Schar | 1,176 | Kummer | 27 |
| Grad | 1,163 | Lie | 26 |
| Doppelpunkt | 113 | Borchardt | 25 |
| Abbildung | 990 | Schubert | 24 |
| Zahl | 971 | Noether | 21 |
The common nouns are not very surprising: they designate the main objects of the research on algebraic surfaces at the end of the 19th century, and associated objects and notions. For instance, Fläche, Punkt, Kurve, Gerade mean “surface,” “point,” “curve” and “line,” while Ordnung and Gleichung mean “order” (a synonym of degree) and “equation.” Two nouns at the end of the list hint at particular topics that we will encounter again later: Abbildung, which can be translated as “representation,” refers to the question of representing a surface on another one (typically, the plane), which can be interpreted nowadays as establishing a birational transformation between these surfaces. The word Zahl (“number”) recalls that many enumerative questions are dealt with in the corpus.
As for the proper nouns, let me just note that the trio composed of Alfred Clebsch, Arthur Cayley and Luigi Cremona dominate the list – they form what Wilhelm Fiedler called “the capital C, which is now […] marching at the head of mathematical Europe in the field of analytic geometry.”16Letter from Fiedler to Cremona, dated March 1867. See [6 G. Israel (ed.), Correspondence of Luigi Cremona (1830–1903). Vol. I. De Diversis Artibus 97, Brepols Publishers, Turnhout (2017) ]. The presence of George Salmon’s name among the most used ones reflects the fact that his famous books on analytic geometry, including the Treatise on the Analytic Geometry of Three Dimensions (four editions in 1862, 1865, 1874, 1882), are widely cited at the time.
It would be possible to deepen such little investigations. Rather, I would like to present two other pictures of the corpus, corresponding to two ways of looking at it. The first one consists in confronting the corpus to another one, in the image of what has been done for Hermite. The second one uses techniques of lexical classification of the texts of the corpus.
3.1 Surfaces vs. invariants
The corpus of comparison that has been chosen is made of all the papers dealing with invariant theory,17In the 19th century, invariants are objects associated with -ary forms. For instance, the discriminant is an invariant of the quadratic form : if is transformed into by an invertible linear transformation of determinant , and if one writes , then for an appropriate integer . written in German and published in Mathematische Annalen during the same period as above, between 1869 and 1898. This algebraic corpus gathers 105 articles and 460,327 words. The authors are 39 in number, among whom 8 also contribute to the theory of surfaces.
A function provided by the software TXM computes the co-occurrents of given terms, that is, words which appear significantly more than others in all the neighbourhoods of the given ones. For instance, let us consider the co-occurrents of the words having Gleichung (“equation”) as their lemma. The first results are given in Table 4 where, for the sake of clarity, articles, propositions and other function words have been excluded. The specificity scores that can be seen in the table measure how characteristic the co-occurrence is.
| Surfaces | |
| Co-occurrent | Spec. |
| Gleichung | 74 |
| Form | 53 |
| Wurzel | 28 |
| setzen | 27 |
| stellen | 24 |
| Elimination | 23 |
| eliminieren | 20 |
| Faktor | 19 |
| befriedigen | 18 |
| erhalten | 17 |
| Koordinate | 17 |
| homogen | 15 |
| genügen | 15 |
Some of the co-occurrents are in the two lists, such as Wurzel (“root”), befriedigen (“to satisfy”) and Elimination. They are part of the standard vocabulary associated with algebraic equations, and their attraction to Gleichung is quite natural.
Among the co-occurrents which are proper to one corpus or the other (or have highly different specificity scores), some recall themes or objects that are characteristic of each mathematical domain. It is the case for homogen and Koordinate for the geometry, and for Lösung, Auflösung and fünft (“solution,” “resolution,” “fifth”) for the invariants, which echoes the publications on invariant theory dealing with the theory of algebraic equations, and especially that of the fifth degree.
The words Seite, links and rechts (“side,” “left” and “right”), which appear only on the invariant table, hint at other aspects of the mathematical work. First, an inspection of these terms within the texts that contain them proves that in the corpus of invariant theory, they almost exclusively refer to the (left or right) side of an equation. Their relative absence in the corpus of algebraic surfaces seems to be tied to a particular kind of mathematical practice: in invariant theory, the pieces and sides of equations are frequently observed, transformed and then re-injected in other equations or equated to zero in order to carry on with a proof. They are also more often the objects of some descriptive comments of the mathematicians who study them. On the contrary, such ways of doings are much scarcer in the corpus of algebraic surfaces.
That the equations are more at the core of the mathematical work in invariant theory can also be seen by studying the specific verbs. As Table 5 shows, almost all the verbs that are specific to the corpus of algebraic surfaces are what I call verbs of geometric action, i.e., verbs of which the subjects or the complements are mathematical objects such as points, curves or surfaces, and which describe the behaviour of such objects: schneiden, treffen, liegen, berühren (“to cut,” “to meet,” “to lie,” “to touch”) are some of them. On the side of invariant theory, the specific verbs refer to another kind of action: for instance, ersetzen, verschwinden, ausdrücken, berechnen, (“to replace,” “to vanish,” “to express,” “to compute”) clearly refer to the lexical field of the algebraic operations.
| Surfaces | |
| Verbs | Spec. |
| schneiden | 273,5 |
| treffen | 179,3 |
| liegen | 176,8 |
| berühren | 171,0 |
| gehen | 115,2 |
| entsprechen | 97,4 |
| abbilden | 64,4 |
| legen | 29,5 |
| begegnen | 28,6 |
| hindurchgehen | 26,4 |
| zerfallen | 25,0 |
This picture is made more complete by examining the common nouns that are specific to the corpuses. Contrary to the case of algebraic surfaces, the corpus of invariants contains, apart from specific nouns referring to the objects proper to the domain, several ones such as Faktor, Formel, Ausdruck (“expression”), Identität and Operation, which are part of the lexicon of the algebraic computations. Moreover, the term Gestalt (“shape”) is also among the nouns that are specific to the corpus of invariant theory, which underscores the fact that observing the aspect of equations and formulas is an important facet of the research of the time.
To finish with the comparison between surfaces and invariants, let me briefly mention that considerable differences exist in the distribution of grammatical categories among the two corpuses. Indeed, the corpus of algebraic surfaces is marked by a very clear over-abundance of common nouns and articles, as well as substituting relative pronouns, indefinite attributive pronouns and commas; in invariant theory, symbols standing for mathematical formulas are legion, while adverbial relative pronouns and periods are also over-represented.
Such imbalances highlight two modes of writing, which are quite different from one another. The corpus of algebraic surfaces contains markedly more sentences whose subjects are the geometric objects themselves, and are often designated by a word of natural language. These sentences are wide and rich of relative propositions, as testifies the over-abundance of commas and of substituting and attributive relative pronouns.18In German, relative clauses that follow a main clause are preceded by a comma. As for invariant theory, sentences are shorter, turned to displayed mathematical formulas and their manipulations: the over-representation of adverbial relative pronouns is explained by a huge number of wo (“where”), used in sentences such as: “This leads to: #, where designates the given invariant.”
These characteristics emerged from a global comparison between the two corpuses. What is striking is that similar differences of writing mathematics can also be found, yet at a more restricted scale, inside the corpus of algebraic surfaces.
3.2 Lexical classes
Another way to investigate the corpus of algebraic surfaces from the textometric point of view, indeed, is to explore the possibilities offered by the functions of lexical classification. Without going into technical details, the idea is just to group into classes the texts that have a similar lexical profile, for instance when taking into account all the common nouns, proper nouns, verbs, adjectives, adverbs and symbols , # that compose them.
The software TXM thus partitions our main corpus into six classes. The aim, then, is to understand if and how such a partition is relevant and significant from a historical perspective. One option is to try to interpret and characterise these classes by combining several viewpoints. Here, only three will be evoked: that of the mere topics of the lexical classes, that of the confrontation with the network analysis of the corpus, and, quite briefly, that of the grammatical imbalances between the classes.
It turns out that the lexical classes coincide to a considerable extent with as so many citation clusters, in the sense that the texts composing each class cite each other a great deal and share some common references, but rarely cite the texts of the other classes (or do so to deprecate them). Such a superposition of the lexical classes and the citation clusters is quite remarkable, considering that each classification is made on the basis of very different criteria: the vocabulary of texts on one hand, the links of citation on the other one. Somehow, this proves that the belonging of a paper to some research dynamics determines its vocabulary, and conversely.
As for the thematics, the six classes can roughly be described as follows – their numbering follows their size, in terms of text numbers. The (very marginal) first one consists of a few papers of Sophus Lie on minimal algebraic surfaces, a topic at the boundary with differential geometry. The second class gathers papers which are devoted to what was called “line geometry” at the time, that is, an approach of space geometry where the basic element is the line (and not the point or, in the dual view, the plane). The third class studies many special surfaces, by tackling a variety of issues such as their singularities, their shape and the making of models of them, typically in plaster (see figure 3).
The fourth class is that of enumerative geometry, the main questions consisting in counting geometrical objects that satisfy given conditions. The fifth one congregates papers falling under what is called the “new synthetic geometry”; in a word, this phrase refers to the avoidance of any recourse to projective coordinates to study algebraic surfaces, and to the need to conceive the latter with “purely geometrical” procedures. The sixth and last class is all about the topic of surface representation, where one tries to find birational correspondences between a given surface and another, and to deduce from this many results on the first surface.
These themes appear clearly in the lists of the words which are specific to each class. As hinted to above, perhaps more surprisingly, the classes happen to possess grammatical specificities as well. For the sake of brevity, I will focus on the fifth and sixth classes, and provide only a few examples of such specificities.
The fifth class, on the new synthetic geometry, is characterised by a colossal over-representation of in-line mathematical formulas, and a more relative under-representation of common nouns and displayed formulas. This is a trace of a way of writing that is very characteristic of these texts, where very long paragraphs without any displayed formula come after one another interminably, the names of geometrical objects being often followed, or even replaced, by a mathematical symbol (see Figure 4).
As for the sixth class, I will just note that it contains an abnormally high number of common nouns, articles and relative pronouns, compared with the other classes. In other words, although at a smaller scale, the same phenomenon that had been seen in the comparison between algebraic surfaces and invariants is observed here: the class is distinguished by an over-representation of long sentences expressed mainly with words of natural language, while only a few mathematical formulas are present in the corresponding texts (see Figure 5).
It is thus noteworthy that even within a relatively small topic, such as that of algebraic surfaces, such different ways of writing theorems and proofs exist, associated with as so many citation clusters and lexical classes.
4 Methodologies
Would it have been possible to detect this phenomenon, or the phenomena which I showcased throughout these pages, without the textometric tools? Probably yes, but maybe with a more conjectural status: one strength of textometry is that it allows to confirm such intuitions. At the same time, using it invites us to explore texts in an original way and to formulate new kinds of research questions, even on corpuses that have been studied by others before.
History of mathematics, just like other research disciplines, evolves with time. The breadth and the depth of the historical knowledge keeps growing. Its norms of rigour change. And the manner of interrogating the past is subject to development as well: trying new methodologies, comparing them to one another and reflecting on them is part and parcel of the historian’s work.
From this point of view, exploiting the tools of textometry to investigate corpuses was also a way for me to investigate the very workability and relevance of using them. As I see it, that some results have been obtained and that new questions arose seem to be a result in itself, and an encouragement to explore this path further.
Acknowledgements. I warmly thank Frédéric Lagoutière for his reading and comments on a first version of this paper. My thanks also go to Ralf Krömer, for having invited me to contribute to the EMS Magazine.
- 1
See for instance [10 L. Lebart, B. Pincemin and C. Poudat, Analyse des données textuelles. Mesure et évaluation 11, Presses de l’Université du Québec (2019) ] for an overview on the topic.
- 2
Do not forget the period!
- 3
See [10 L. Lebart, B. Pincemin and C. Poudat, Analyse des données textuelles. Mesure et évaluation 11, Presses de l’Université du Québec (2019) , pp. 122–123] and the reference to Pierre Lafon’s works given there.
- 4
A forthcoming special issue of Revue d’histoire des mathématiques is devoted to this bicentenary. It will include the paper [9 F. Lê, On Charles Hermite’s style. Rev. Histoire Math., to appear ], which corresponds to the present section. More generally, for a rich and deep study of numerous aspects of Hermite’s work, see the publications of Catherine Goldstein, such as [3 C. Goldstein, The Hermitian form of reading the disquisitiones. In The shaping of arithmetic after C. F. Gauss’s Disquisitiones arithmeticae, pp. 377–410, Springer, Berlin (2007) , 4 C. Goldstein, Charles Hermite’s stroll through the Galois fields. Rev. Histoire Math. 17, 211–270 (2011) ].
- 5
It must be emphasised, though, that the two historians were looking at two distinct pieces of Hermite’s publications, which possibly led to different appreciations. My own approach considers at once almost all the published articles of Hermite.
- 6
The numerical side of the problem is linked to the question of lexical diversity. This question is investigated in [9 F. Lê, On Charles Hermite’s style. Rev. Histoire Math., to appear ], together with that of lexical sophistication.
- 7
Because of the capital C, Comparaison is not the same as comparaison from the viewpoint of word counting, even though the two words have the same lemma.
- 8
Throughout this paper, all the French and German terms that are not translated are supposed to have a transparent meaning in English.
- 9
“Almost two years have passed, and I have not yet responded to the letter, filled with kindness, that you made me the honor to write to myself. I am coming today to beg you to forgive my long negligence, and to express all the joy that I have felt by seeing for myself some room in the collection of your works. Having been away from work for a long time, I have been very touched by such a testimony of your benevolence. Allow me, Sir, to believe that it will not abandon me […].” The French words in italics are the hapaxes.
- 10
“Mr. Kronecker, by giving it as the analytic expression of one of his theorems, had obviously foreseen the meaning that it would receive in the theory of elliptic functions, and, in this respect, I cannot but admire the insight he demonstrated.”
- 11
The examination of the terms that are specific to Jordan is interesting because many of them are related to the proof by contradiction, with hypothèse, absurde, inadmissible, contraire, and the French adverbs of negation ne, pas. A systematic counting of this kind of reasoning shows that it is used 599 times by Jordan, and only 35 times by Hermite…. This curious feature, however, is not related to the question of style as I wished to understand.
- 12
Jordan’s corpus is also abnormally rich in conditional, subjunctive and, to a lesser extent, imperfect indicative. This imbalance is to be linked to the over-use of proofs by contradiction that we alluded to above.
- 13
“In general, this system will thus contain only a fraction of the substitutions of the primitive system.”
- 14
“This remark being made, I am going to study closer the quotients ….”
- 15
The results of the present section come from [8 F. Lê, Le théorie des surfaces algébriques dans les Mathematische Annalen à l’épreuve de la textométrie (1869–1898). Rev. Histoire Math. 28, 1–45 (2022) ].
- 16
Letter from Fiedler to Cremona, dated March 1867. See [6 G. Israel (ed.), Correspondence of Luigi Cremona (1830–1903). Vol. I. De Diversis Artibus 97, Brepols Publishers, Turnhout (2017) ].
- 17
In the 19th century, invariants are objects associated with -ary forms. For instance, the discriminant is an invariant of the quadratic form : if is transformed into by an invertible linear transformation of determinant , and if one writes , then for an appropriate integer .
- 18
In German, relative clauses that follow a main clause are preceded by a comma.
References
- F. Brechenmacher, La controverse de 1874 entre Camille Jordan et Leopold Kronecker. Rev. Histoire Math. 13, 187–257 (2007)
- A. Clebsch, Ueber die Abbildung algebraischer Flächen, insbesondere der vierten und fünften Ordnung. Math. Ann. 1, 253–316 (1869)
- C. Goldstein, The Hermitian form of reading the disquisitiones. In The shaping of arithmetic after C. F. Gauss’s Disquisitiones arithmeticae, pp. 377–410, Springer, Berlin (2007)
- C. Goldstein, Charles Hermite’s stroll through the Galois fields. Rev. Histoire Math. 17, 211–270 (2011)
- S. Heiden, The TXM platform: Building open-source textual analysis software compatible with the TEI encoding scheme. In Proceedings of the 24th Pacific Asia Conference on Language, Information and Computation, pp. 389–398, Institute for Digital Enhancement of Cognitive Development, Waseda University, Tokyo, Japan (2010)
- G. Israel (ed.), Correspondence of Luigi Cremona (1830–1903). Vol. I. De Diversis Artibus 97, Brepols Publishers, Turnhout (2017)
- F. Lê, “Are the genre and the Geschlecht one and the same number?” An inquiry into Alfred Clebsch’s Geschlecht. Historia Math. 53, 71–107 (2020)
- F. Lê, Le théorie des surfaces algébriques dans les Mathematische Annalen à l’épreuve de la textométrie (1869–1898). Rev. Histoire Math. 28, 1–45 (2022)
- F. Lê, On Charles Hermite’s style. Rev. Histoire Math., to appear
- L. Lebart, B. Pincemin and C. Poudat, Analyse des données textuelles. Mesure et évaluation 11, Presses de l’Université du Québec (2019)
- K. Rohn, Ein Beitrag zur Theorie der biplanaren und uniplanaren Knotenpunkte. Math. Ann. 22, 124–144 (1883)
- F. Schur, Ueber die durch collineare Grundgebilde erzeugten Curven und Flächen. Math. Ann. 18, 1–32 (1881)
- M. Serfati, Quadrature du cercle, fractions continues et autres contes : Sur l’histoire des nombres irrationnels et transcendants aux XVIIIe et XIXe siècles. Brochure A.P.M.E.P. 86 (1992)
Cite this article
François Lê, Words, history and mathematics. Eur. Math. Soc. Mag. 130 (2023), pp. 26–35
DOI 10.4171/MAG/153