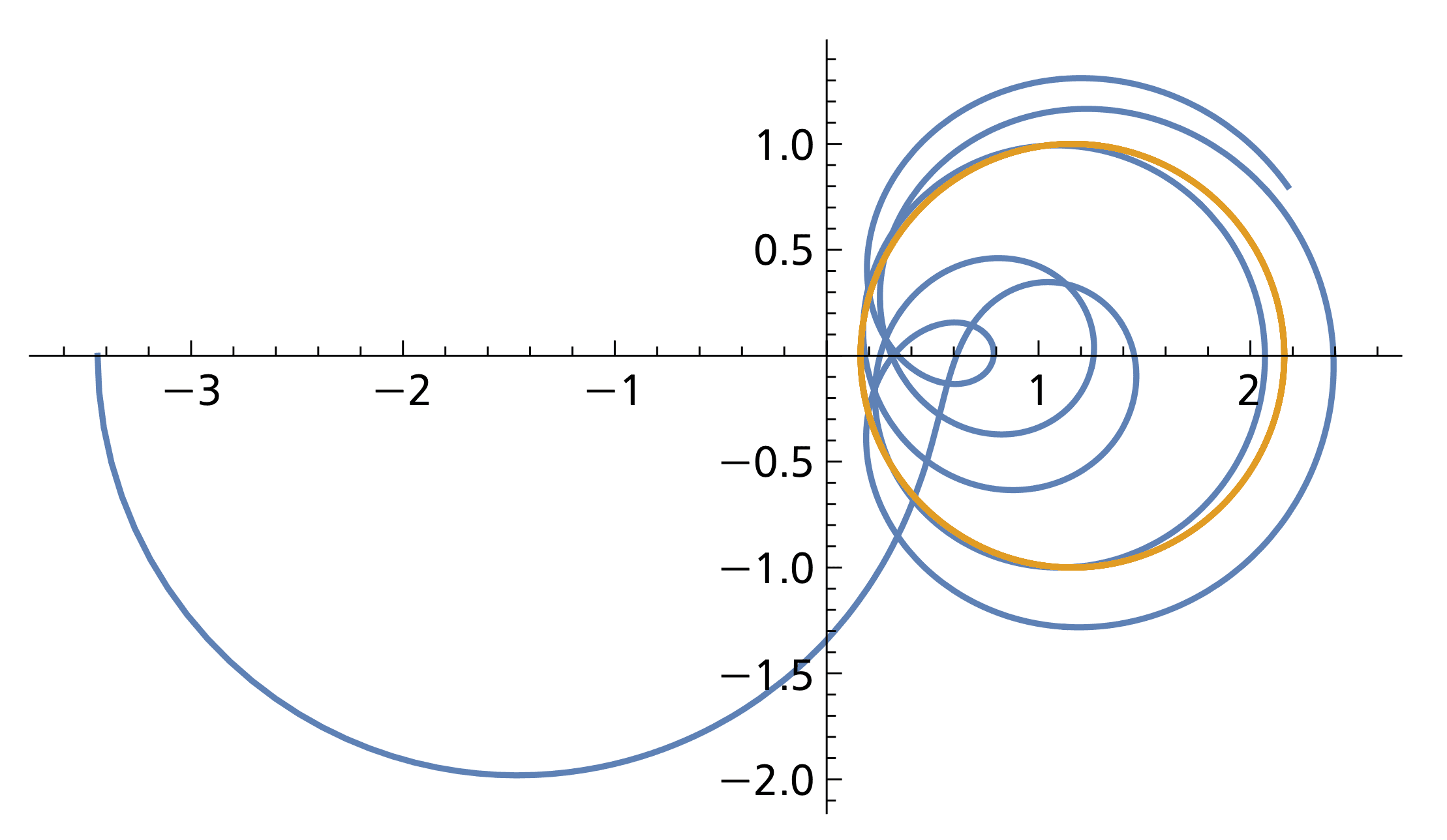An atlas for all plane curves

1 Curves generated by the Riemann zeta-function

Curves appear naturally in life, perhaps not as ideal objects, as Euclid defined a line as “a length without breadth” in his Elements, but as orbits of planets, trajectories in physics and technology, or drawings in art. Taking into account their variety, it might be surprising that one can find them all realized in a single curve. Following Tolkien, we may state this also as a “Lord of the Curves” poem:

One Curve to rule them all, One Curve to find them, One Curve to bring them all, And in the plane bind them.

Of course, our statement above needs to be clarified. Here and in the sequel we consider only finite and smooth curves on the plane, meaning that for each of them there exists a parametrization of the form

such that $\gamma$ has a non-vanishing first derivative and a continuous second derivative (see [⁠5⁠ M. P. do Carmo, Differential geometry of curves and surfaces. Prentice-Hall, Englewood Cliffs, NJ (1976) ]); this includes line segments, ellipses, and many more curves that easily come to mind. The single curve that realizes all these smooth curves, however, is an artifact and has to be infinite for obvious reasons. In this respect, our theorem below has some implications to our understanding of infinity.

This infinite curve originates from the Riemann zeta-function, defined by

where $s=\sigma +it$ with the imaginary unit $i=\sqrt{-1}$ (in the upper half-plane) is a complex variable with real part $\sigma >0$. The complex-valued function $\zeta (s)$ plays a central role in analytic number theory and the distribution of prime numbers in particular (see [⁠9⁠ H. L. Montgomery and R. C. Vaughan, Multiplicative number theory. I. Classical theory. Cambridge Studies in Advanced Mathematics 97, Cambridge University Press, Cambridge (2007) ]). For our result, we need to allow deviations by a quantity as small as desired. The mathematical language allows for a precise formulation:

Here, of course, we regard any curve on the Euclidean plane, via ${\mathbb{R}}^2\simeq \mathbb{C}$, also as a curve on the complex plane.

In view of the positive lower density for the set of real shifts $\tau >0$ that lead to the desired approximation of the target function, it follows that any plane curve appears infinitely often, up to a tiny error bounded by $\epsilon$, in any curve $\zeta (\sigma +i\mathbb{R})$ with any fixed $\sigma \in (1/2,1)$ (even with positive lower density). In this sense, the zeta-function provides a single plane curve that contains all the plane curves with an error too small to be seen with the naked eye! Note that the Planck length is about $1.6\cdot 10^{-36}$ meters and, according to quantum mechanics, one cannot see anything smaller than this tiny quantity.

Hence, the values of the zeta-function on any vertical line in the right open half of the critical strip provide an atlas for plane curves (where atlas should be understood as in geography, rather than as in the mathematical context of manifolds).

We note that, in view of the universality theorem, the target function just needs to be continuous if $\mathcal{K}$ has empty interior. This even allows to approximate space-filling curves like the Peano curve, for which a continuous representation (⁠1⁠) exists (see [⁠10⁠ H. Sagan, Space-filling curves. Universitext, Springer-Verlag, New York (1994) ] and Figure ⁠2⁠ for the Peano curve as the limit of an iteration). This Peano curve maps the unit interval $[0,1]$ onto the unit square $[0,1{]}^2$. On the contrary, the map $t\mapsto \zeta (\sigma +it)$ is differentiable and, therefore, if $t$ is restricted to a bounded interval, the corresponding curve necessarily has finite length. That nevertheless the approximation of a space-filling curve is possible follows from the inaccuracy hidden behind the epsilon.

Is it possible to extend these results further? To answer this question we recall that, more than a century ago, Bohr (the mathematician Harald, younger brother of the physicist Niels) and Courant [⁠3⁠ H. Bohr and R. Courant, Neue Anwendungen der Theorie der Diophantischen Approximationen auf die Riemannsche Zetafunktion. J. Reine Angew. Math. 144, 249–274 (1914) ] proved that $\zeta (\sigma +i\mathbb{R})$ is dense in $\mathbb{C}$ for every fixed $\sigma \in (1/2,1]$ (which means that one can find a value $\zeta (\sigma +it)$ for some real $t$ in every neighbourhood of every point of the complex plane). Of course, this result also follows from universality (by choosing a constant target function). For the critical line, however, it is unknown whether $\zeta (1/2+i\mathbb{R})$ is dense in the complex plane or not. Universality applies neither to the critical line (because of too many zeros of $\zeta$), nor to any vertical line $\sigma +i\mathbb{R}$ with $\sigma >1$ (because of the absolute convergence of the defining series (⁠2⁠)). These limitations also hold for the approximation of plane curves, which is obvious for $\sigma >1$ (since then $|\zeta (\sigma +it)|\le \zeta (\sigma )$); for $\sigma \le 1/2$, however, this follows from a result of Gonek and Montgomery [⁠7⁠ S. M. Gonek and H. L. Montgomery, Spirals of the zeta function I. In Analytic number theory, pp. 127–131, Springer, Cham (2015) ], who showed that the curvature of $t\mapsto \zeta (1/2+it)$ is negative for $t\ge 3$ and something similar holds for $\sigma <1/2$ as well. The latter result is conditional subject to the truth of the famous, yet unproven, Riemann Hypothesis that

This open conjecture is one of the seven Millennium Problems in mathematics.

We conclude with a related problem in the universe of numbers. Does every finite pattern of digits appear in the infinite decimal fraction expansion of the circle number $\pi =3.1415926535897\dots$? There exist real numbers with this property, for example the Champernowne constant $0.1234567891011\dots$ (built from the positive integers in ascending order) and it has been proven that almost all real numbers have this property (such numbers are called normal; see [⁠4⁠ K. Dajani and C. Kraaikamp, Ergodic theory of numbers. Carus Mathematical Monographs 29, Mathematical Association of America, Washington, DC (2002) ]); however, the case of special numbers is difficult and wide open in the case of $\pi$.

A more detailed account of our study with additional results in this context will appear elsewhere.

Acknowledgements. With this short note the authors want to express their gratitude to the EMS for the financial support of the conference “Universality, Zeta-Functions, and Chaotic Operators” at Centre international de rencontres mathématiques in Luminy in August 2023. We are also grateful to the referee for carefully reading our note. The first author was supported by the Austrian Science Fund (FWF): project M 3246-N.

Athanasios Sourmelidis has graduated from the University of Patras in 2013 and completed his doctoral studies at the University of Würzburg in 2019. He is currently a postdoc researcher in the Insitute of Analysis and Number Theory in the Technical University of Graz, being awarded a Lise Meitner fellowship from the Austrian Science Fund (FWF). His research interests lie on the field of analytic number theory with focus on the value-distribution of zeta- and $L$-functions. sourmelidis@math.tugraz.at Jörn Steuding studied and received his PhD in Hannover; later he was a postdoc in Frankfurt and Madrid. Since 2006 he has been a professor of mathematics at the University of Würzburg. His research focuses on aspects of analytic number theory and, in particular, the value-distribution of the Riemann zeta-function and related functions. steuding@mathematik.uni-wuerzburg.de

References

1. J. Andersson, Lavrent’ev’s approximation theorem with nonvanishing polynomials and universality of zeta-functions. In New directions in value-distribution theory of zeta and L-functions, pp. 7–10, Shaker Verlag, Aachen (2009)
2. B. Bagchi, The statistical behaviour and universality properties of the Riemann zeta-function and other allied Dirichlet series, PhD Thesis, Calcutta, Indian Statistical Institute (1981)
3. H. Bohr and R. Courant, Neue Anwendungen der Theorie der Diophantischen Approximationen auf die Riemannsche Zetafunktion. J. Reine Angew. Math. 144, 249–274 (1914)
4. K. Dajani and C. Kraaikamp, Ergodic theory of numbers. Carus Mathematical Monographs 29, Mathematical Association of America, Washington, DC (2002)
5. M. P. do Carmo, Differential geometry of curves and surfaces. Prentice-Hall, Englewood Cliffs, NJ (1976)
6. S. M. Gonek, Analytic properties of zeta and L-functions. PhD Thesis, University of Michigan (1979)
7. S. M. Gonek and H. L. Montgomery, Spirals of the zeta function I. In Analytic number theory, pp. 127–131, Springer, Cham (2015)
8. S. N. Mergelyan, Uniform approximations to functions of a complex variable. (In Russian.) Uspehi Matem. Nauk (N.S.) 7, 31–122 (1952); English translation: Am. Math. Soc. Transl. 101 (1954)
9. H. L. Montgomery and R. C. Vaughan, Multiplicative number theory. I. Classical theory. Cambridge Studies in Advanced Mathematics 97, Cambridge University Press, Cambridge (2007)
10. H. Sagan, Space-filling curves. Universitext, Springer-Verlag, New York (1994)
11. J. Steuding, Value-distribution of L-functions. Lecture Notes in Mathematics 1877, Springer, Berlin (2007)
12. S. M. Voronin, Theorem on the “universality” of the Riemann zeta-function. (In Russian.) Izv. Akad. Nauk SSSR Ser. Mat. 39, 475–486, 703 (1975); English translation: Math. USSR, Izv. 9 (1975), 443–453 (1976)