The Indian tradition in mathematics is long and glorious. It dates to the earliest times, and indeed many of the Indian discoveries from a period starting 5000 years ago correspond rather naturally to modern mathematical results. Celebration of Indian mathematics needs to consider the personalities among ancient mathematicians who laid a solid foundation for modern thinking. Our main purpose here is, by presenting very briefly some of the main contributions of ancient Indian mathematicians and astronomers, to argue and convince the reader that before the great Ramanujan, there have been thousands of years of rich mathematical discoveries in India and those personalities’ work also needs to be honored on Indian Mathematics Day.
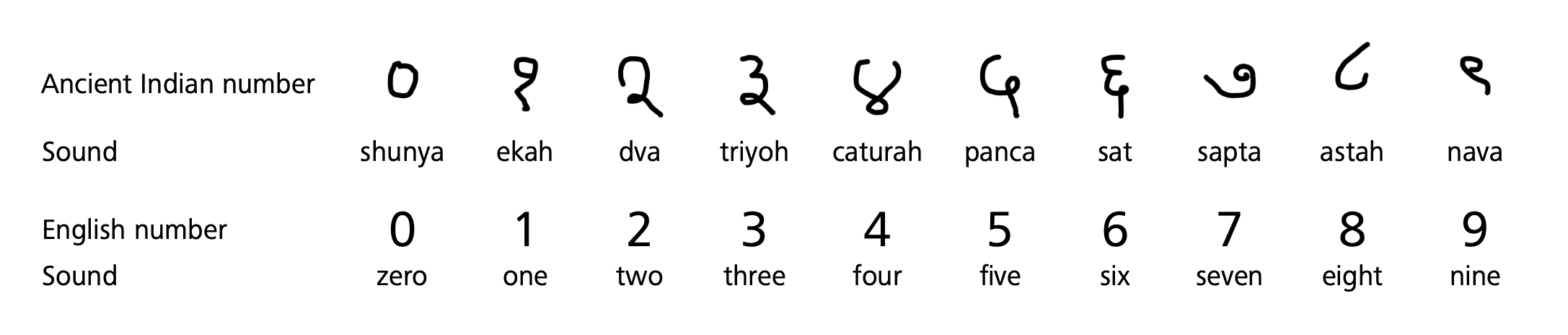
Table 1. Sanskrit and English numerals to and their sounds.
The government of India announced in 2012 that every year, Indian mathematician Srinivasa Ramanujan’s birthday, December 22, will be celebrated as national mathematics day.1Prime Minister’s speech at the 125th Birth Anniversary Celebrations of Ramanujan at Chennai: https://archive.is/20120729041631/http://pmindia.nic.in/speech-details.php?nodeid=1117 (accessed on April 15, 2023). The year 2012 was the great Ramanujan’s 125th birth anniversary. The government of India released a commemorative stamp on that occasion as well. Brilliant contributions in number theory and combinatorics by Ramanujan are well known [2 G. E. Andrews and B. C. Berndt, Ramanujan’s lost notebook. Part V. Springer, Cham (2018) , 1 G. E. Andrews and B. C. Berndt, Ramanujan’s lost notebook. Part I. Springer, New York (2005) , 13 S. Ramanujan, The lost notebook and other unpublished papers. Springer-Verlag, Berlin; Narosa Publishing House, New Delhi (1988) , 16 A. S. R. Srinivasa Rao, Ramanujan and religion. Notices Amer. Math. Soc. 53, 1007–1008 (2006) ]. However, deep astronomical and mathematical developments in India are several thousand years older than Ramanujan. In this comment, we try to recollect a few gems of the ancient Indian mathematics and its mathematicians who did fundamental work in number systems, mathematics of astronomy, calculus, etc., over more than 5000 years.
Our main purpose for writing this article is to argue and convince that, while giving Ramanujan’s brilliant achievements during the past 125 years their due place, reducing the Mathematics Day in India to the celebration of Ramanujan’s birthday (who was born in the 19th century) is somewhat short-sighted. Our goal is to make sure Indian Mathematics Day is seen as a celebration of thousands of years of deep-rooted mathematical thought processes and discoveries since the times of Shulba sutra. Moreover, it should also be devoted to celebrating many very strong mathematicians, such as, say, Harish Chandra, who have come since Ramanujan’s time.
The origins of the mathematics that emerged in the Indian subcontinent can be seen around the Shulba sutra period, around 1200 BCE to 500 BCE. During this period the numbers up to were counted (in Vedic Sanskrit this number was referred to as Paradham). The Vedic period mathematics was confined to the geometry of fire-altars and astronomy, and these concepts were used to perform rituals by the priests. Some of the famous names from that era are Baudhayana, Apastamba, and Katyayana. In Table 1 we describe Sanskrit sounds and their corresponding English numerals. Indian mathematics also introduced the decimal number system that is in use today and the concept of zero as a number. The concepts of sine (written as jaya in Sanskrit) and cosine (cojaya), negative numbers, arithmetic, and algebra were found in ancient Indian mathematics [6 B. Datta and A. N. Singh, History of Hindu mathematics: A source book. Part I: Numerical notation and arithmetic. Part II: Algebra. Asia Publishing House, Bombay–Calcutta–New Delhi–Madras–London-New York (1962) ]. The mathematics developed in India was later translated and transmitted to China, East Asia, West Asia, Europe, and Saudi Arabia. The classical period of Indian mathematics was often attributed to the interval from 200 CE to 1400 CE, during which works of several well-known mathematicians, like Varahamihira, Aryabhata, Brahmagupta, Bhaskara, and Madhava have been translated into other languages and transmitted outside the sub-continent.
The number systems present since the Vedic days, especially since the Sukla Yajurveda and their Sanskrit sounds, were as follows: (Eka), (Dasa), (Sata), (Sahasra), (Aayuta), (Laksa or Niyuta), (Koti), (Sanku or Paraardha), (Maha Sanku), (Vrnda), (Samudra), (Maha-ogha).
In addition to the number systems of ancient India, still today in India are heard the popular “Vishnu Sahasra Nama Stotra,” which dates back to the Mahabharata epic. In this, there is a verse that sounds like Sahasra “Koti Yugadharine Namah.” If we translate this verse, then, as we saw above, Sahasra means , and Koti means , so a simple translation of the phrase Sahasra Koti could mean . The entire phrase has been interpreted in different ways. We do not list here all possible interpretations and confine ourselves to number systems.
The deep investigations in astronomy and the solar system, geometry, and ground-breaking mathematical calculations by ancient and medieval great scholars in India, for example, Baudhayana, Varahamihira, Aryabhata, Bhaskara I & II, Pingala, Madhava, and many more, are well known (see [10 G. G. Joseph, The crest of the peacock: Non-European roots of mathematics. 2nd ed., Princeton University Press, Princeton, NJ (2000) , 7 B. R. Evans, The development of mathematics throughout the centuries: A brief history in a cultural context. John Wiley & Sons, New York (2014) , 5 B. Dâjî, Brief notes on the age and authenticity of the works of Âryabhaṭa, Varâhamihira, Brahmagupta, Bhaṭṭ otpala, and Bhâskarâchârya. Journal of the Royal Asiatic Society 1, 392–418 (1865) ] and [17 A. S. R. Srinivasa Rao and S. G. Krantz, Dynamical systems: From classical mechanics and astronomy to modern methods. J. Indian Inst. Sci. 101, 419–429 (2021) , p. 423]).
It seems that celebrating national mathematics day in India only as part of Ramanujan’s birthday is confining the glory and celebration of Indian mathematics to a little over 100 years of the past. Schools and colleges across India have celebrated Ramanujan’s birthday for many decades, but that is different from exclusively limiting national day only to the great Ramanujan.
A good deal can be written on ancient scholar’s work from India; material on this can be found, for example in [8 R. C. Gupta, T. A. Sarasvati Amma (c. 1920–2000): A great scholar of Indian geometry. Bhāvanā 3 (2019) , 12 K. Plofker, Mathematics in India. Princeton University Press, Princeton, NJ (2009) , 15 T. A. Sarasvati Amma, Geometry in ancient and medieval India. Motilal Banarsidass, Delhi (1979) , 6 B. Datta and A. N. Singh, History of Hindu mathematics: A source book. Part I: Numerical notation and arithmetic. Part II: Algebra. Asia Publishing House, Bombay–Calcutta–New Delhi–Madras–London-New York (1962) , 3 A. Bürk, Das Āpastamba-Śulba-Sūtra. Zeitschrift der Deutschen Morgenländischen Gesellschaft 55, 543–591 (2001) ]. In this opinion piece, we highlight only a few of them.
Shulba sutras were believed to have started in India around 2000 BCE through verbal usage. Their compilation in Sanskrit started perhaps 1000 years later by Baudhayana then by Manava, Apastamba, Katyayana and consisted of geometric-shaped fire-altars for performing ancient Indian rituals [3 A. Bürk, Das Āpastamba-Śulba-Sūtra. Zeitschrift der Deutschen Morgenländischen Gesellschaft 55, 543–591 (2001) , 12 K. Plofker, Mathematics in India. Princeton University Press, Princeton, NJ (2009) ]. Some of these sutras also contain the statements of Pythagorean theorems and triples. For example, Apastamba provided the following triples:
for constructing fire-altars [15 T. A. Sarasvati Amma, Geometry in ancient and medieval India. Motilal Banarsidass, Delhi (1979) ].
These sutras can be used to find the approximate value of [15 T. A. Sarasvati Amma, Geometry in ancient and medieval India. Motilal Banarsidass, Delhi (1979) , 12 K. Plofker, Mathematics in India. Princeton University Press, Princeton, NJ (2009) ], using the expression
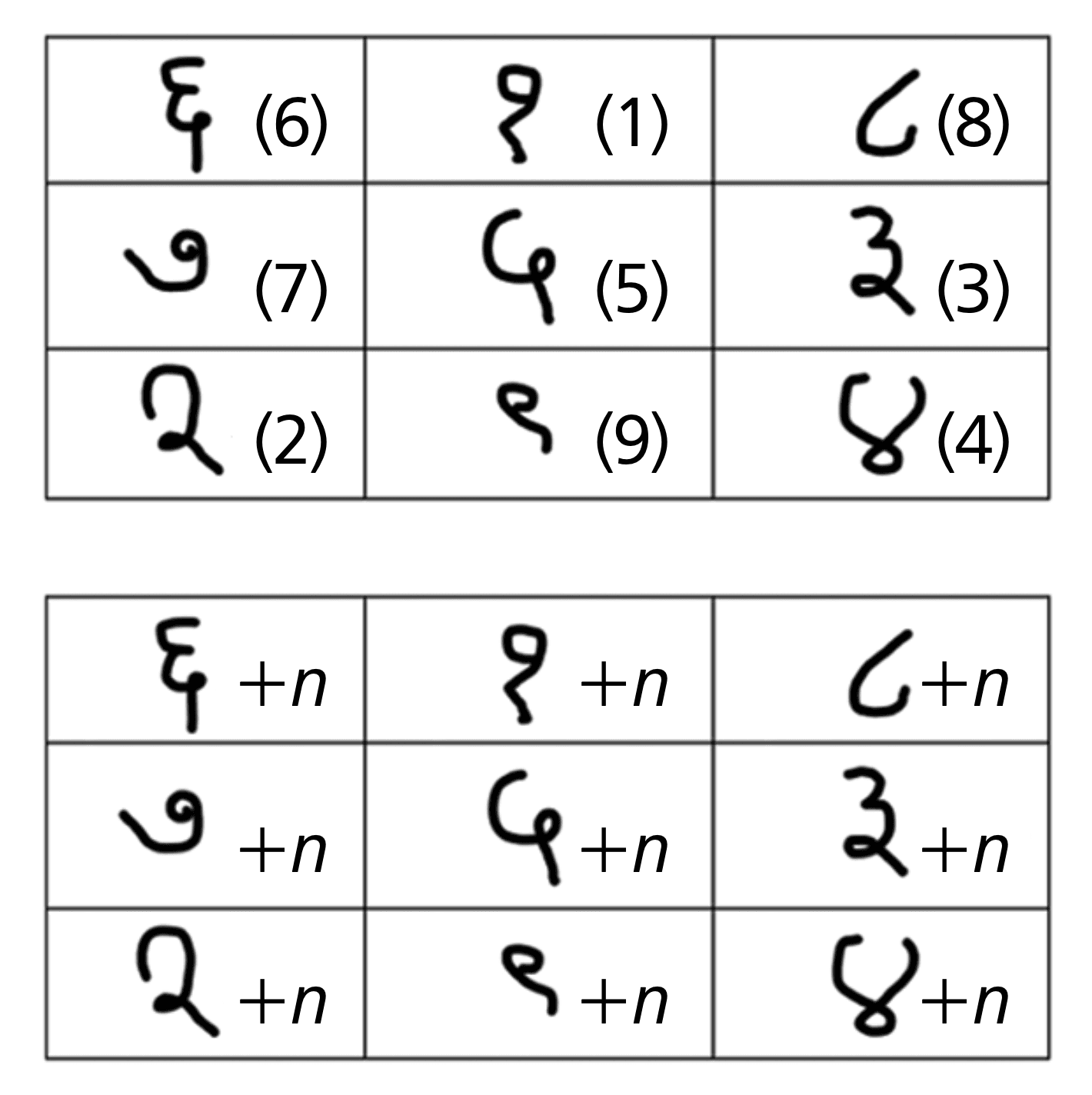
In the Vedic period astrology (Jyotisha) of India, the magic squares (anka-yantra) were used to please and worship nine planets of the solar system [9 R. C. Gupta, Mystical mathematics of ancient planets. Indian J. Hist. Sci. 40, 31–53 (2005) , 18 G. P. H. Styan and K. L. Chu, An illustrated introduction to some old magic squares from India. In Combinatorial matrix theory and generalized inverses of matrices, pp. 227–252, Springer, New Delhi (2013) ]. Figure 1 is about ancient magic squares for the Sun and the other eight planets in our solar system.
In the 5th century CE, Aryabhata calculated, among many other things, that the moon orbit takes 27.396 days, the value of , etc. He is believed to have started the study of properties of sine and cosine in trigonometry.
According to [12 K. Plofker, Mathematics in India. Princeton University Press, Princeton, NJ (2009) ], the Leibniz infinite series
was known in the works of Indian mathematician Madhava, who lived three centuries before Leibniz.
In the 12th century CE, Bhaskara described in his famous book Bijaganita the rules of algebraic operations on positive, negative signs, rules of zero (shunya), and infinity (anantam). His book also shows how to obtain solutions to intermediate equations of the first degree [14 K. Ramasubramanian, T. Hayashi and C. Montelle, (eds.), Bhāskara-prabhā. Sources Stud. Hist. Math. Phys. Sci., Springer, Singapore (2019) ]. Bhaskara’s book titled Siddhanta siromani provided a detailed account of Indian astronomy and its development. Computations of the planetary movements, shapes of planets, rotation axis, lunar month days, etc., were explained in detail. See Figure 2. Pavuluri Mallana translated Mahavira’s Ganitasarasamgraha from Sanskrit in the 11th century to another ancient indian language, Telugu; Joseph [11 G. G. Joseph, Indian mathematics: Engaging with the world from ancient to modern times. World Scientific Publishing, Hackensack, NJ (2016) ] thinks that this stood as a role model for other subsequent translations. Bhaskara’s Lilavati Ganitam was for the first time translated from Sanskrit to Telugu in the 12th century by Eluganti Peddana [4 P. Chenchiah and R. M. Bhujanga, A history of Telugu literature. The Association Press, Calcutta; Oxford University Press, London (1928) ], and into English first in 1816 by John Taylor, then in 1817 by Henry Thomas Holbrooke, who was considered as the first European Sanskrit scholar.
What we advocate in this piece is for an exposition of deep-rooted mathematical knowledge in India, and not an exhaustive account of all possible results and conclusions. Several of the ancient texts in the language Sanskrit are either lost or preserved in museums.
Bhaskaracarya / Wikimedia Commons / CC BY-SA 4.0
Srinivasa Ramanujan’s work undoubtedly shines as part of modern Indian mathematics but thousands of years ancient mathematical discoveries, the introduction of various branches of pure and applied mathematics needs a proper representation in any celebration of India’s contribution to world mathematics.
We hope that this short list of significant examples will convince the readers as well as the decision makers of the need to incorporate and celebrate all the rich past and contemporary history of Indian mathematics during the Indian Mathematics Day.
Acknowledgements. We are thankful to the reviewer for the comments that helped us to make the point in the article clearer. We are also thankful to Prof. Ralf Krömer, editor of the EMS Magazine, and the editorial staff and copyeditor of EMS Press for their edits to our article.
- 1
Prime Minister’s speech at the 125th Birth Anniversary Celebrations of Ramanujan at Chennai: https://archive.is/20120729041631/http://pmindia.nic.in/speech-details.php?nodeid=1117 (accessed on April 15, 2023).
- 2
This book is available for free at https://upload.wikimedia.org/wikipedia/commons/7/75/Lilavatiganitamu00bhassher.pdf. © Sundarayya Vignana Kendram, Bagh Lingampally, Hyderabad, India
References
- G. E. Andrews and B. C. Berndt, Ramanujan’s lost notebook. Part I. Springer, New York (2005)
- G. E. Andrews and B. C. Berndt, Ramanujan’s lost notebook. Part V. Springer, Cham (2018)
- A. Bürk, Das Āpastamba-Śulba-Sūtra. Zeitschrift der Deutschen Morgenländischen Gesellschaft 55, 543–591 (2001)
- P. Chenchiah and R. M. Bhujanga, A history of Telugu literature. The Association Press, Calcutta; Oxford University Press, London (1928)
- B. Dâjî, Brief notes on the age and authenticity of the works of Âryabhaṭa, Varâhamihira, Brahmagupta, Bhaṭṭ otpala, and Bhâskarâchârya. Journal of the Royal Asiatic Society 1, 392–418 (1865)
- B. Datta and A. N. Singh, History of Hindu mathematics: A source book. Part I: Numerical notation and arithmetic. Part II: Algebra. Asia Publishing House, Bombay–Calcutta–New Delhi–Madras–London-New York (1962)
- B. R. Evans, The development of mathematics throughout the centuries: A brief history in a cultural context. John Wiley & Sons, New York (2014)
- R. C. Gupta, T. A. Sarasvati Amma (c. 1920–2000): A great scholar of Indian geometry. Bhāvanā 3 (2019)
- R. C. Gupta, Mystical mathematics of ancient planets. Indian J. Hist. Sci. 40, 31–53 (2005)
- G. G. Joseph, The crest of the peacock: Non-European roots of mathematics. 2nd ed., Princeton University Press, Princeton, NJ (2000)
- G. G. Joseph, Indian mathematics: Engaging with the world from ancient to modern times. World Scientific Publishing, Hackensack, NJ (2016)
- K. Plofker, Mathematics in India. Princeton University Press, Princeton, NJ (2009)
- S. Ramanujan, The lost notebook and other unpublished papers. Springer-Verlag, Berlin; Narosa Publishing House, New Delhi (1988)
- K. Ramasubramanian, T. Hayashi and C. Montelle, (eds.), Bhāskara-prabhā. Sources Stud. Hist. Math. Phys. Sci., Springer, Singapore (2019)
- T. A. Sarasvati Amma, Geometry in ancient and medieval India. Motilal Banarsidass, Delhi (1979)
- A. S. R. Srinivasa Rao, Ramanujan and religion. Notices Amer. Math. Soc. 53, 1007–1008 (2006)
- A. S. R. Srinivasa Rao and S. G. Krantz, Dynamical systems: From classical mechanics and astronomy to modern methods. J. Indian Inst. Sci. 101, 419–429 (2021)
- G. P. H. Styan and K. L. Chu, An illustrated introduction to some old magic squares from India. In Combinatorial matrix theory and generalized inverses of matrices, pp. 227–252, Springer, New Delhi (2013)
Cite this article
Steven G. Krantz, Arni S. R. Srinivasa Rao, Ancient Indian mathematics needs an honorific place in modern mathematics celebration. Eur. Math. Soc. Mag. 130 (2023), pp. 36–39
DOI 10.4171/MAG/139