Mathematics as seen by an artist: Inspiring mathematical objects

This article presents a series of hundreds of paintings produced by the painter Reg Alcorn⁠¹⁠https://www.reg-alcorn.fr since 2017, entitled Transitions, as well as the two mathematical objects he uses to determine the structure of the paintings in this series, one ancient and the other more recent, the Truchet tile and the Ulam spiral.

The title of our article echoes the one previously published by the same authors in the same journal [⁠19⁠ S. Vinatier and R. Alcorn, Les maths vues par un artiste: une expérience de diffusion de la culture mathématique via l’art et l’histoire de l’art. Gaz. Math. 144 48–53 (2015) ], in which we presented an initiative by the IREM of Limoges⁠²⁠Institute of Research on Mathematics Education. and the artist Reg Alcorn, in collaboration with the CCSTI⁠³⁠Center for Scientific, Technical and Industrial Culture. of Limousin Récréasciences, to disseminate mathematical culture through artistic media: several periods in the history of art were used to illuminate and highlight mathematical concepts (Antiquity and proportion, the Arab-Andalusian Middle Ages and paving, the Renaissance and perspective). Reg Alcorn’s art was then serving the topics explored in this initiative by producing paintings that were used to explain the artistic and mathematical concepts involved. In the series Transitions, the artist reverses the perspective: he chooses objects from his study of mathematics and its history and uses them for his personal artistic explorations, resulting in unique works with purely artistic aims.⁠⁴⁠That is why Reg Alcorn is listed as author of this article, almost entirely written by the first author and based essentially on the artistic investigation of the second.

This may well be an effect of the work previously carried out jointly by Reg Alcorn and the IREM of Limoges, which greatly enriched the mathematical (or scientific) and artistic knowledge of those involved. The artist has immersed himself in numerous mathematical works (aimed at the general public, students and even researchers), which has aroused in him a genuine fascination for some of the objects or concepts encountered. So much so that, after a maturing phase, two of them, from very different eras and contexts, found themselves interwoven in the series of paintings Transitions.

We will describe them in turn in the next two sections, taking the opportunity to develop certain mathematical or historical aspects beyond what would be strictly necessary to understand the artist’s use of them, in the hope that these digressions will be of interest to our readers. Without pretending to be historians and keeping to the surface of mathematical theories, we thought it would be a good idea to present these objects through the circumstances of their discovery, surprising in both cases, to show how they were apprehended and how they relate to key mathematical issues at the beginning of the 18th century or today. Finally, for those who would rather focus on the links between art and mathematics, the definitions of the objects at the start of Sections ⁠1⁠ and ⁠2⁠ should suffice to appreciate Reg Alcorn’s recipe for the paintings in his Transitions series, which we will give in the ⁠third⁠ and final section.

1 Truchet tiles

The first mathematical ingredient in the series Transitions, the Truchet tile, is itself at the crossroads of science and art, as we shall see. It takes us back to an important milestone in the development of combinatorics, when Father Sébastien Truchet (1657–1729), mathematician, typographer, “clockmaker, great canal specialist, inventor of countless machines (cannons, tree-transplanting machines, sundials, etc.) including the famous mechanical tables of Marly” [⁠1⁠ J. André, De Pacioli à Truchet: trois siècles de géométrie pour les caractères. In 4000 ans d’histoire des mathématiques: les mathématiques dans la longue durée. IREM de Rennes, Rennes, France (2002) https://bibnum.publimath.fr/IWH/IWH02004.pdf], became interested in the different relative positions of two squares, both divided into two colors: given two identical squares, split in two along the diagonal, with one half white and the other black (see Figure ⁠2⁠), in how many ways can they be arranged in relation to each other?

This question is systematically discussed by Truchet in a 1704 paper for the Académie royale des sciences [⁠18⁠ S. Truchet, Mémoire sur les combinaisons. In Mémoires de mathématique et de physique tirés des registres de l’Académie Royale des Sciences, pp. 363–372, Paris (1704) https://gallica.bnf.fr/ark:/12148/bpt6k3486m/f517].

Combinatorics and tessellations. Before presenting his answer, let us note that Truchet’s aim is to study ornamental pavings that can be made from this tile (he proposes a selection of them in his dissertation). This is indeed the motivation he himself gives for his study, by way of an introduction to his Mémoire [⁠18⁠ S. Truchet, Mémoire sur les combinaisons. In Mémoires de mathématique et de physique tirés des registres de l’Académie Royale des Sciences, pp. 363–372, Paris (1704) https://gallica.bnf.fr/ark:/12148/bpt6k3486m/f517, p. 363]:

On the last trip I made to the Orléans Canal by order of His Royal Highness, I found in a castle named La Motte S. Lyé, 4 leagues from Orléans, several square fayence tiles divided into two colors by a diagonal line, which were intended to tile a chapel & several other rooms. In order to form pleasant patterns & shapes by arranging these tiles, I first examined how many ways two of these tiles could be joined together, always arranging them in a chessboard.

This work, in which chance and curiosity seem to have played an important role, makes him a precursor in the history of the study of tessellations, which was little practiced by scientists before the 19th century and the development of crystallography (although he had Kepler⁠⁵⁠Johannes Kepler, German astronomer (1571–1630). as a very illustrious predecessor in this field [⁠10⁠ P. Esperet and D. Girou, Coloriage du pavage dit ‘de Truchet.’ Cahiers GUTenberg 31, 5–18 (1998) http://www.numdam.org/item/CG_1998___31_5_0/]). It is also based on a combinatorial study, a field to which his contribution is described in [⁠16⁠ C. S. Smith and P. Boucher, The tiling patterns of Sebastien Truchet and the topology of structural hierarchy. Leonardo 20, 373–385 (1987) , p. 377] as follows:

Truchet’s treatise is of considerable importance for it is in essence a graphical treatment of combinatorics, a subject that, under the influence of Pascal, Fermat and Leibniz, was at the forefront of mathematics at the time.

The originality of his approach, which links combinatorics and tessellations, is also underlined by André and Girou [⁠3⁠ J. André and D. Girou, Father Truchet, the typographic point, the Romain du roi, and tilings. TUGboat 20, 8–14 (1999)https://www.tug.org/TUGboat/Articles/tb20-1/tb62andr.pdf, p. 11].

Truchet’s treatise. He begins by presenting 64 combinations obtained by considering that the two tiles are different: the first has four possible orientations, as does the second, which can moreover be placed against any of the four sides of the first. This number of combinations is immediately reduced to 32 if we no longer differentiate the two tiles, and further reduced to ten if, in addition, we disregard the pairs of tiles that only differ by rotation.⁠⁶⁠See [⁠16⁠ C. S. Smith and P. Boucher, The tiling patterns of Sebastien Truchet and the topology of structural hierarchy. Leonardo 20, 373–385 (1987) , p. 384, note 5.] for a discussion of these reductions. These combinations and reductions are illustrated by two tables in [⁠18⁠ S. Truchet, Mémoire sur les combinaisons. In Mémoires de mathématique et de physique tirés des registres de l’Académie Royale des Sciences, pp. 363–372, Paris (1704) https://gallica.bnf.fr/ark:/12148/bpt6k3486m/f517], reproduced in Figure ⁠3⁠.

The paper [⁠15⁠ L. Rougetet and M. Boutin, Jeu de parquet et combinaisons, ou la double patrimonialisation d’un objet et de ses savoirs mathématiques. Philos. Sci. (Paris) 26, 91–121 (2022) ], in addition to examining the patrimonialization in various ways (mathematical, playful, pedagogical) of the Truchet tiles, rightly notes that ten equals the number of combinations with possible repetition of two objects among four. This equality does not seem immediately meaningful to us: if we have to choose two of the four squares, with possible repetition, to form the patterns considered by Truchet, and if we can arrange them in a line, regardless of pairwise rotation, the order in which we arrange them has an importance ($ab$ does not produce the same result as $ba$, regardless of pairwise rotation) and some of the resulting patterns are identical after rotation, such as $ab$ and $dc$ ($a$, $b$, $c$, $d$ denote the tiles obtained by successive quarter-turn rotations of the Truchet tile in Figure ⁠2⁠, see also Figure ⁠9⁠). However, these two effects compensate each other: the involutions defined on $\{a,b,c,d{\}}^2$ by $(x,y)\mapsto (y,x)$ and $(x,y)\mapsto (r(y),r(x))$, where $r$ is the “half-turn” that changes $a$ to $c$ and $b$ to $d$, both have four fixed points and six pairs of related couples, i.e., they have the same number of orbits; yet those of the first involution correspond to combinations with possible repetition, and those of the second to patterns of two tiles regardless of pairwise rotation.

The “graphical treatment” of the combinatorial problem evoked by [⁠16⁠ C. S. Smith and P. Boucher, The tiling patterns of Sebastien Truchet and the topology of structural hierarchy. Leonardo 20, 373–385 (1987) ] also consists in the spatial organization of the possible configurations, which reflects the systematic study carried out by Truchet: in each column of his Table I (see Table I in Figure ⁠3⁠), the “first” tile is in the orientation drawn in the first row, while that of the “second” varies according to the row; finally, the four relative positions appear in the four corners of each box of the table. The arrangement of the configurations shows the completeness of the initial search, so all that remains is to identify those that are alike according to the set criteria (Tables II and III in Figure ⁠3⁠).

The author adds that he has begun work on combinations of three, four and five bisected tiles, but that he is not satisfied with it and intends to publish it at a later date (which will not be the case). Of course, complexity increases very rapidly with the number of tiles, as can be seen in Reg Alcorn’s paintings, if only because there are several spatial arrangements of three, four or five tiles: in a line, in an ‘L,’ in a square, in a ‘T,’ in a cross…

Lastly, Truchet presents seven plates of tiling patterns obtained by connecting some of the 64 tile combinations he has listed: they include 24 tilings of size $12\times 12$ tiles and six of size $24\times 18$, chosen from among 100 completed tilings, themselves selected among patterns in “too large a quantity to report them all” [⁠18⁠ S. Truchet, Mémoire sur les combinaisons. In Mémoires de mathématique et de physique tirés des registres de l’Académie Royale des Sciences, pp. 363–372, Paris (1704) https://gallica.bnf.fr/ark:/12148/bpt6k3486m/f517, p. 364].

Another reverend of the same religious order as Father Truchet, Dominique Doüat, took up this work and published a Method for making an infinite number of drawings in 1722 [⁠8⁠ D. Doüat, Méthode pour faire une infinité de desseins différens, avec des carreaux mi-partis de deux couleurs par une ligne diagonale. Jacques Quillau, Imprimeur Juré de l’Université, Paris (1722) https://gallica.bnf.fr/ark:/12148/bpt6k5823204r] containing 72 tilings produced with Truchet’s bisected tiles. We show one of his plates in Figure ⁠4⁠.

Sources. For all Truchet-related information, Jacques André’s website⁠⁷⁠https://jacques-andre.fr/faqtypo/truchet/ is an invaluable mine of documents and references, in addition to his own publications on the subject [⁠1⁠ J. André, De Pacioli à Truchet: trois siècles de géométrie pour les caractères. In 4000 ans d’histoire des mathématiques: les mathématiques dans la longue durée. IREM de Rennes, Rennes, France (2002) https://bibnum.publimath.fr/IWH/IWH02004.pdf, ⁠3⁠ J. André and D. Girou, Father Truchet, the typographic point, the Romain du roi, and tilings. TUGboat 20, 8–14 (1999)https://www.tug.org/TUGboat/Articles/tb20-1/tb62andr.pdf]. In particular, he mentions the possibility of consulting Truchet’s treatise [⁠18⁠ S. Truchet, Mémoire sur les combinaisons. In Mémoires de mathématique et de physique tirés des registres de l’Académie Royale des Sciences, pp. 363–372, Paris (1704) https://gallica.bnf.fr/ark:/12148/bpt6k3486m/f517] on the Bibliothèque nationale de France’s Gallica documentary database (with plates of engravings ahead of the memoir), as well as in English translation in [⁠16⁠ C. S. Smith and P. Boucher, The tiling patterns of Sebastien Truchet and the topology of structural hierarchy. Leonardo 20, 373–385 (1987) ]. Doüat’s work [⁠8⁠ D. Doüat, Méthode pour faire une infinité de desseins différens, avec des carreaux mi-partis de deux couleurs par une ligne diagonale. Jacques Quillau, Imprimeur Juré de l’Université, Paris (1722) https://gallica.bnf.fr/ark:/12148/bpt6k5823204r] (which André makes available, preceded by a rich introduction) and the article Carreau (Architecture) [⁠7⁠ D. Diderot, Carreau s. m. (Architecture). In Encyclopédie ou dictionnaire raisonné des sciences, des arts et des métiers. Vol. II., pp. 699–701, Briasson, Paris (1752) https://gallica.bnf.fr/ark:/12148/bpt6k50534p/f705] from Diderot and d’Alembert’s Encyclopédie, discussed below, are also available on Gallica in facsimile. For all these documents, links to Gallica are provided in the bibliography. André also points to the transcribed version of the Encyclopédie on the ARTFL project site,⁠⁸⁠https://encyclopedie.uchicago.edu see also the Édition Numérique Collaborative et CRitique de l’Encyclopédie which combines transcription and facsimile of the first edition.⁠⁹⁠https://enccre.academie-sciences.fr/encyclopedie/

On Jacques André’s website, one can also find a document [⁠2⁠ J. André, Les planches de pavages de Truchet. (2010)https://jacques-andre.fr/faqtypo/truchet/truchet-planches.pdf] featuring illustrations of Truchet tilings from several sources: by Truchet himself, in his treatise [⁠18⁠ S. Truchet, Mémoire sur les combinaisons. In Mémoires de mathématique et de physique tirés des registres de l’Académie Royale des Sciences, pp. 363–372, Paris (1704) https://gallica.bnf.fr/ark:/12148/bpt6k3486m/f517] and in the Description des arts et métiers, an encyclopedia whose project was launched by Colbert, directed in particular by Réaumur, to which he contributed⁠¹⁰⁠The plates date from 1705, but this encyclopedia only began to be published in fascicules from 1761 onwards.; by Doüat [⁠8⁠ D. Doüat, Méthode pour faire une infinité de desseins différens, avec des carreaux mi-partis de deux couleurs par une ligne diagonale. Jacques Quillau, Imprimeur Juré de l’Université, Paris (1722) https://gallica.bnf.fr/ark:/12148/bpt6k5823204r]; from the Encyclopédie [⁠7⁠ D. Diderot, Carreau s. m. (Architecture). In Encyclopédie ou dictionnaire raisonné des sciences, des arts et des métiers. Vol. II., pp. 699–701, Briasson, Paris (1752) https://gallica.bnf.fr/ark:/12148/bpt6k50534p/f705], whose Table des 64 combinaisons is reproduced (while pointing out an error); and from a later work by an architect (Lemaire, 1862), from which two similarly inspired plates are featured.

In the Encyclopédie. Diderot faithfully reproduces the contents of Truchet’s treatise in the article ‘Carreau’ of the Encyclopédie [⁠7⁠ D. Diderot, Carreau s. m. (Architecture). In Encyclopédie ou dictionnaire raisonné des sciences, des arts et des métiers. Vol. II., pp. 699–701, Briasson, Paris (1752) https://gallica.bnf.fr/ark:/12148/bpt6k50534p/f705]: he presents the 64 combinations obtained by differentiating the two tiles under consideration, as well as the reductions to 32 and ten combinations we have described. He goes on to add a final (double) reduction, consisting of identifying identical combinations by color inversion or by flipping (the latter identification is described as follows: “if we suppose them traced on transparent paper, we will see some of them by looking through the paper, the same way we see the others on the paper itself” [⁠7⁠ D. Diderot, Carreau s. m. (Architecture). In Encyclopédie ou dictionnaire raisonné des sciences, des arts et des métiers. Vol. II., pp. 699–701, Briasson, Paris (1752) https://gallica.bnf.fr/ark:/12148/bpt6k50534p/f705, p. 700]). This leaves only four classes of combinations. He concludes the reduction as follows:

Perhaps if we had looked for a way of arranging the combinations of these tiles on paper, we would have found a law that would have dispensed with the previous enumeration: but this is what no one has yet attempted, nor the combination of several tiles, and even less the combination of tiles of several colors.

It is noteworthy that Diderot concludes this study by highlighting a number of gaps in the knowledge of the time on this subject, which can be considered open questions to the scientific community; and it is just as noteworthy that the artist Reg Alcorn happily exploited a variant of this last gap, by declining at will the colors of the halves of the squares he laid out on his canvas, taking full advantage of his artistic freedom and finding there a field in which to express his talent. To describe the way he arranges them, we’ll introduce a second, more recent and complex mathematical object a little further down, in Section ⁠2⁠.

Another enumeration of combinations. Before that, let us try to answer Diderot’s first question and show how we can arrive at the four terminal combinations more quickly than by Truchet’s and Diderot’s successive reductions. We start with two empty squares, and there is, disregarding rotation, only one way to assemble them side by side:

We now add a diagonal to each: there are, a priori, two possible choices of the diagonal in each of the two squares, so four possibilities; but they are two by two identical by flipping, which leaves us with the two configurations:

We now need to color one half out of two in each square. Again, in each of the two configurations, there are two choices for the half to be colored in each of the two squares, i.e., a priori four possibilities for each configuration, which would make eight possibilities in total. But each of these is accompanied by one where the colors are reversed, so if we identify the identical combinations by reversing the colors, this divides the number of possibilities by two, and we get the following four combinations:

The result points the way to another, even more straightforward demonstration: allowing rotation, the two tiles can be arranged in a line and, allowing flipping and color inversion, we get the following pattern first.

It remains to choose the second motif from the possible four.

2 The Ulam spiral

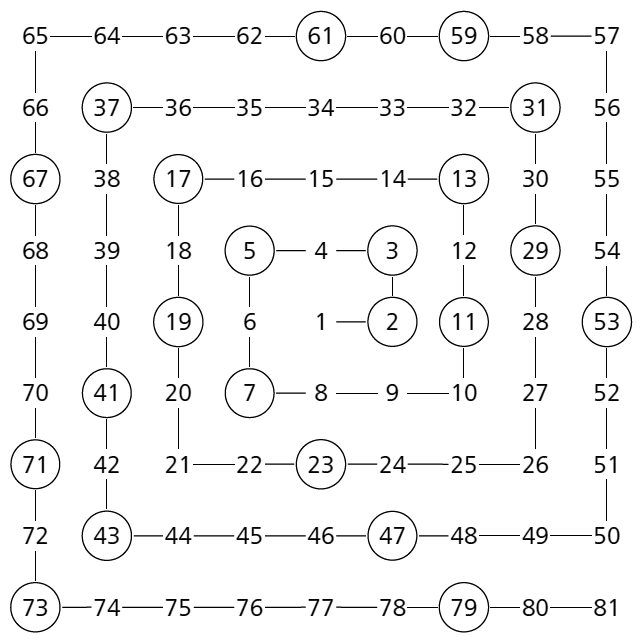
Now we come to our second mathematical ingredient. Creativity from boredom. According to Martin Gardner,⁠¹¹⁠American writer (1914–2010), great popularizer of mathematics. who tells the story in an article for the popular science magazine Scientific American [⁠11⁠ M. Gardner, Mathematical games: The remarkable lore of the prime numbers. Scientific American 210.3 120–130 (1964) ], the mathematician Stanislaw Ulam, bored while attending a conference in the autumn of 1963, began to draw a grid on a sheet of paper to represent a chessboard; changing his mind, he began to number the intersections starting from the center of the grid and spiraling around it in an anti-clockwise direction; then he began to circle the prime numbers and, to his great surprise, saw lines forming along the diagonals (Figure ⁠5⁠).

As Gardner points out, this fact is not very significant for a small spiral, insofar as all the integers belonging to a line of diagonal direction have the same parity, all the primes (except one⁠¹²⁠Or rather except two!) are odd and the density of primes is high among the smallest integers. So in the $9\times 9$ spiral shown in Figure ⁠5⁠, the 21 odd primes are distributed among just 41 possible positions, forming lines parallel to the diagonals…

Consolidation. However, Ulam was able to verify with two collaborators, Stein and Wells [⁠17⁠ M. L. Stein, S. M. Ulam and M. B. Wells, A visual display of some properties of the distribution of primes. Amer. Math. Monthly 71, 516–520 (1964) ], that the observed phenomenon was not confined to small integers, but appeared to be a general property of prime numbers. To do this, they used the MANIAC II computer at their research institution, the Los Alamos laboratory of the University of California, as well as magnetic tapes containing tables of prime numbers, to obtain spirals covering much larger numbers of integers (photos of spirals obtained with 10000 and 65000 integers are reproduced in [⁠11⁠ M. Gardner, Mathematical games: The remarkable lore of the prime numbers. Scientific American 210.3 120–130 (1964) ], they resemble the spiral on the right in Figure ⁠5⁠, at different scales).

As impressive as these images of unexpected prime number alignments may be, so much so that Ulam’s spiral made the front page of the issue of Scientific American in which Gardner’s article appeared, Ulam and his collaborators explain that they are due to the large numbers of prime values taken by certain quadratic functions of the integers, of the type $n\mapsto a{n}^2+bn+c$ with $a,b,c\in \mathbb{Z}$, such as Euler’s famous formula

for which all the values for $n$ between 0 and 39 are distinct primes (!) and which takes about 47.5% of prime values among its values up to 10000000 [⁠17⁠ M. L. Stein, S. M. Ulam and M. B. Wells, A visual display of some properties of the distribution of primes. Amer. Math. Monthly 71, 516–520 (1964) , p. 520]. Ulam and his colleagues have identified other quadratic forms with high rate $\tau$ of prime values up to 10000000 including

However, the reporter of the article pointed out that the integer values of the first are included in the sequence of numbers produced by Euler’s formula (on even integers):

The rate of $46.6\%$ of prime values among values up to $10^7$ of $E(2n+42)$ is roughly the rate of prime values among values up to $10^7$ of $E$ at even integers; by comparison with the overall rate, that at odd integers must be $48.4\%$. We do not know whether this slight difference between the rates for even and odd integers is asymptotically confirmed. We shall see below that our knowledge of the asymptotic behavior of the number of prime values of polynomials is essentially conjectural.

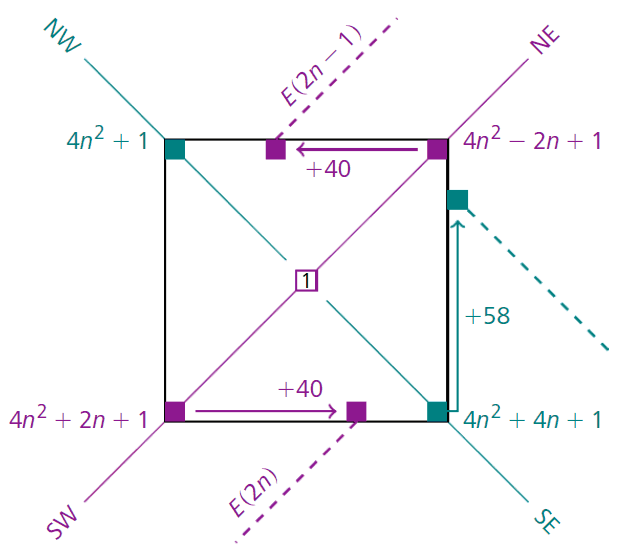
Alignments parallel to semi-diagonals. It is easy to position oneself in Ulam’s spiral by observing (on Figure ⁠5⁠) that the piece of spiral that goes from 1 to $(2n+1{)}^2$ for an integer $n$ forms a square, each side of which contains $2n+1$ integers, centered at 1, with the number $(2n+1{)}^2=4n^2+4n+1$ in the bottom right-hand corner. We immediately deduce the expressions of the numbers at the other corners of the square of size $2n+1$. They form the four semi-diagonals starting from 1, and are plotted on Figure ⁠6⁠.

For example, the numbers of the southeast semi-diagonal are the squares of odd integers, of the form $4n^2+4n+1$, so that the values of the second quadratic form mentioned in (⁠2⁠), $(4n^2+4n+1)+58$, occupy, for $n$ large enough, the translation of this semi-diagonal by 58 upwards (we turn counter-clockwise, following Ulam’s example).

Similarly, the numbers of the northeast (resp. southwest) semi-diagonal are integers of the form $4n^2-2n+1$ (resp. $4n^2+2n+1$), so that the values of Euler’s formula (⁠1⁠) at odd integers, $E(2n-1)=(4n^2-2n+1)+40$ (resp. at even ones, $E(2n)=(4n^2+2n+1)+40$), occupy, for $n$ large enough, the translation of the northeast (resp. southwest) semi-diagonal by 40 to the left (resp. right).

We therefore see in Figure ⁠7⁠ alignments of prime numbers in directions parallel to the diagonals, produced by the quadratic forms (⁠1⁠) and (⁠2⁠), which according to [⁠17⁠ M. L. Stein, S. M. Ulam and M. B. Wells, A visual display of some properties of the distribution of primes. Amer. Math. Monthly 71, 516–520 (1964) ] take many prime values at integers, up to $10^7$. To find out whether this phenomenon persists beyond this value, when the size of the spiral is further increased, we need to look at the asymptotic behavior of these polynomials.

Asymptotic behavior. Hardy and Littlewood’s “Conjecture F” (1923) predicts the asymptotic behavior of the number of values of the variable, natural number less than a positive real $x$, for which $r$ polynomials with integer coefficients simultaneously take prime values, in the form of a constant depending on the respective polynomials multiplied by the function $x/(\ln x{)}^r$. See [⁠5⁠ K. Conrad, Hardy–Littlewood constants. In Mathematical properties of sequences and other combinatorial structures (Los Angeles, CA, 2002), pp. 133–154, Kluwer Acad. Publ., Boston, MA (2003) ] for more details in the general case.

In [⁠13⁠ M. J. Jacobson, Jr. and H. C. Williams, New quadratic polynomials with high densities of prime values. Math. Comp. 72, 499–519 (2003) ], Jacobson and Williams study polynomials of degree 2 that generalize Euler’s formula, of the form $f_A(x)=x^2+x+A$ with $A\in \mathbb{Z}$. Denoting by $P_A(n)$ the number of prime values taken by $f_A$ at natural integers at most $n$ and by $\Delta =1-4A$ the discriminant of $f_A$, they state Conjecture F as follows:

where the Hardy–Littlewood constant$C(\Delta )$ is defined by the Euler product:

It is a product on odd primes $p$, with $(\frac{\Delta }{p})$ denoting the Legendre symbol for $\Delta$ on $p$. One can check by calculation (via integration by parts) or by using the formulation of the conjecture given in [⁠5⁠ K. Conrad, Hardy–Littlewood constants. In Mathematical properties of sequences and other combinatorial structures (Los Angeles, CA, 2002), pp. 133–154, Kluwer Acad. Publ., Boston, MA (2003) ] (note that the constant is defined here by an Euler product over all primes) that the equivalence (⁠3⁠) can also be written as

Under this conjecture, the constant $C(\Delta )$ has a decisive influence on the asymptotic behavior of the number of prime values taken by $f_A$.

The numerical results support Conjecture F. For $A=41$, we have $C(-163)=3.3197732$ and the Euler polynomial $x^2+x+41$ takes 87% of prime values up to 100 (estimated value using (⁠4⁠): $72\%$) and $47.5\%$ up to $3162=\lfloor \sqrt{10^7}\rfloor$ according to [⁠17⁠ M. L. Stein, S. M. Ulam and M. B. Wells, A visual display of some properties of the distribution of primes. Amer. Math. Monthly 71, 516–520 (1964) ] (estimated value: $41.2\%$). We know from [⁠13⁠ M. J. Jacobson, Jr. and H. C. Williams, New quadratic polynomials with high densities of prime values. Math. Comp. 72, 499–519 (2003) ] that this rate is $22.08\%$ up to $10^7$ (estimated value: $20.6\%$) and that, for $A^{\prime }=3399714628553118047$, we have

and $25.17\%$ of prime values up to $10^7$; even if this rate is lower than the estimated value ($33.3\%$), it is higher than the corresponding rate for $A=41$, which seems to corroborate the fact that a larger Hardy–Littlewood constant corresponds asymptotically to a larger number of prime values.

The value of $C(\Delta )$ associated with the integer $A^{\prime }$ considered above was the largest known before the calculations presented in [⁠13⁠ M. J. Jacobson, Jr. and H. C. Williams, New quadratic polynomials with high densities of prime values. Math. Comp. 72, 499–519 (2003) ]. The prepublication [⁠4⁠ H. Cohen, High precision computations of Hardy–Littlewood constants. Preprint, (1998) https://oeis.org/A221712/a221712.pdf, §4.2] explains how to determine a high-precision approximate value of $C(\Delta )$ and also gives as an example the much smaller value for $A=75$, $C(-299)=0.3109767$. The maximum value for $C(\Delta )$ found by Jacobson and Williams is $5.65726388$ (under the generalized Riemann hypothesis), corresponding to an integer with 71 decimal digits.

Arithmetic progressions. One may also see in [⁠5⁠ K. Conrad, Hardy–Littlewood constants. In Mathematical properties of sequences and other combinatorial structures (Los Angeles, CA, 2002), pp. 133–154, Kluwer Acad. Publ., Boston, MA (2003) ] that, while the general Conjecture F is supported by numerical calculations and sieve methods, it is only proven in the case of one polynomial of degree 1: it then comes down to Dirichlet’s arithmetic progressions theorem (in the quantitative version proved by de La Vallée Poussin), which states that for all coprime integers $a,b$ the polynomial $ax+b$ takes infinitely many prime values (uniformly distributed in the invertible classes modulo $a$). More precisely, denoting by $P_{a,b}(n)$ the number of prime values of $ax+b$ at natural numbers at most $n$, we have the equivalence

where $\phi$ is the Euler totient function; this confirms the equivalence (⁠4⁠) and specifies the Hardy–Littlewood constant in this particular case. This result in degree 1 also has a graphic interpretation: let us write the integers in a rectangular grid of given width, starting at the top left and filling the grid line by line. The numbers $an+b$ for $n\in \mathbb{N}$ then lie on a straight line (cut into pieces by the grid), so the corresponding prime values again produce alignments.

In all other cases, we cannot even prove that the number whose asymptotic behavior the conjecture predicts, tends towards infinity with $x$. For example, the integer values of the two polynomials $x$ and $x+2$ that are simultaneously prime are the twin primes, and we do not know whether they are infinite or not.

In degree 1, we know even more thanks to Green and Tao’s Theorem [⁠12⁠ B. Green and T. Tao, The primes contain arbitrarily long arithmetic progressions. Ann. of Math. (2) 167, 481–547 (2008) ]: not only do arithmetic progressions contain an infinite number of primes, but there are arithmetic progressions of primes of any length: for any natural number $k$, there are primes $p_1$, $p_2$, …, $p_k$ which are consecutive terms of an arithmetic sequence, i.e., such that the differences $p_{i+1}-p_i$ are constant. The proof of the theorem is not constructive, and finding such sequences is difficult, as the common difference is likely to be very large.⁠¹³⁠The current record is for $k=27$, set by Gahan in 2019, see https://oeis.org/A327760.

Small variable values. Several authors have studied the first values of other polynomials of degree 2, with smaller coefficients and for smaller values of the variable, and therefore more likely to explain the lines that show on the small-scale plots of Ulam’s spiral. The polynomial of degree 2:

holds the current record for the number of consecutive distinct prime values: 45 (between $-33$ and 11, established by Ruby in 1989); it therefore surpasses the Euler polynomial (only two other polynomials are known for which this is true, due to Fung and dating from 1988). In addition, it takes 49 distinct prime values in 50 consecutive values of the variable, with five possible starts between $-41$ and $-33$. See the introduction and Section 2 of [⁠9⁠ F. Dress and M. Olivier, Polynômes prenant des valeurs premières. Experiment. Math. 8, 319–338 (1999) ] for details.

In that paper, Dress and Olivier present the results of their numerical search for polynomials with a large number of prime values, counting only the distinct prime values taken for 50, 100, 500 or 1000 consecutive values of the variable. In the latter case, they significantly improve on previous results with the polynomials

• $x^2+x-1354363$: 698 prime values (from $x=1139$ to $x=2138$);

• $x^2+x-752293$ and $4x^2+2x-349513$: 685 prime values;

• $4x^2+2x-501229$: 684 prime values.

Note that $36x^2+18x-1801=E(6x+1)-1844$ and that, for any $A\in \mathbb{Z}$:

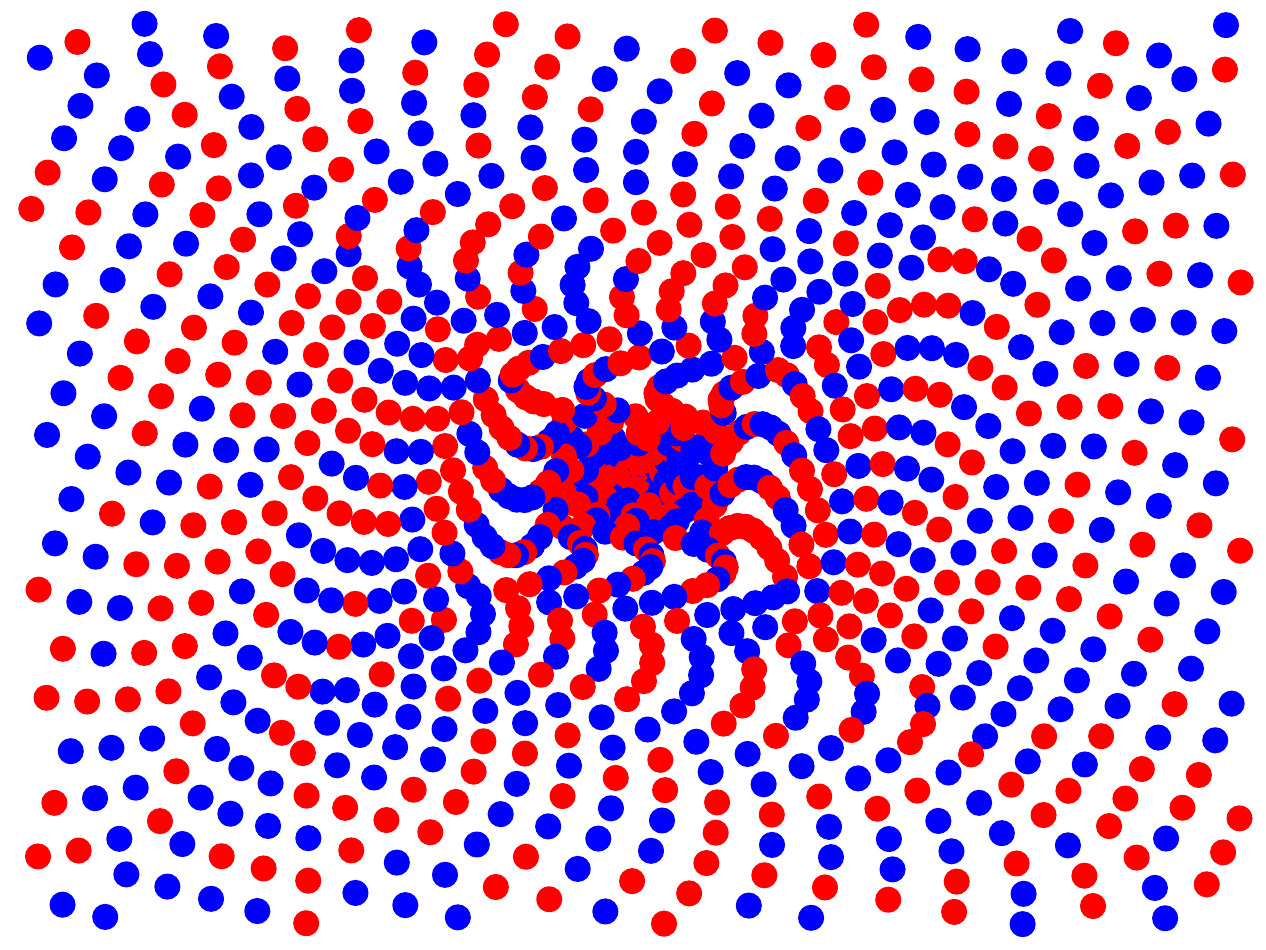
so that the polynomials we have just discussed, like Euler’s formula, produce alignments in Ulam’s spiral parallel to the northeast and/or southwest semi-diagonals, provided the value of the variable is sufficiently large. A number of other polynomials taking a large number of prime values appear in [⁠9⁠ F. Dress and M. Olivier, Polynômes prenant des valeurs premières. Experiment. Math. 8, 319–338 (1999) ], which are neither of this form nor of the second identified by Ulam and his collaborators (⁠2⁠), including in degree 2. A precise description of the alignments that may appear in Ulam’s spiral is found in [⁠14⁠ S. Marquès and S. Vinatier, Alignments in Ulam’s spiral. (Work in progress) (2025) ], along with figures showing the distribution of values of some of these other polynomials (in the spiral-wound plane as for Ulam’s spiral), such as the one in Figure ⁠8⁠.

3 The genesis of the Transitions series

At the origin of the Transitions series, there is … a desire for geometry! Like several other artists before him, Reg Alcorn was looking for a geometric process to structure the canvases of his new series. Among the artists who followed this path, some of them having links to mathematics, are Mondrian (1872–1944), Kandinsky (1866–1944), Vasarely (1906–1997), Morellet (1926–2016) and, of course, Picasso (1881–1973) and the Cubist movement in general, for the analysis of perception and the geometrization of space.

3.1 Reg Alcorn’s approach

For his series of paintings Transitions, the artist has developed a systematic procedure⁠¹⁴⁠Although he might occasionally deviate from it, over the course of the two hundred paintings in this series. determined by the two mathematical ingredients presented above: Truchet tiles and Ulam’s spiral. In fact, to the four tiles obtained by turning the Truchet tile in Figure ⁠2⁠, he adds two: an all-white square and an all-black square. It is convenient to codify them as in Figure ⁠9⁠.

He then chooses a sequence of some of these tiles, of any length, for example $daadb$, and – instead of arranging it in a line, which would look like this:

– he winds it in a spiral from the center of the painting, repeating the sequence identically until the painting is filled. In our example, the first steps are:

or the first occurrence of the sequence, then:

and

with two, three, four and five occurrences respectively (a complete square is obtained). Figure ⁠10⁠ shows the result with 20 occurrences of the sequence (i.e., 100 tiles forming a square of 10$\times$10).

We realize immediately that the very simple process we have implemented quickly produces complex, unpredictable patterns, even though they are determined by the sequence chosen at the outset and, in particular, are highly dependent on its length. For example, it can be seen in Figure ⁠11⁠ that sequences with lengths in multiples of four produce much more regular patterns than the example of length five chosen above, notably because the numbers belonging to any of the pattern’s semi-diagonals are always congruent modulo 4. This means that the same tile can be found all along (resp., at least every other time) a semi-diagonal of a pattern produced by a sequence of length four (resp., eight). It is worth noting that, even in this case, reversing two tiles will produce very different effects.

An atlas of sequences is in preparation, which promises to show the incredible richness of this process, complementing the numerous canvases created by the artist, more examples of which are given below.

3.2 Playing with color

Once the sequence has been selected and the configuration of the painting determined, Reg Alcorn’s art consists in choosing the colors that will replace the black and white of the areas drawn by the completed paving, accentuating particular motifs, sometimes revealing different ones depending on the distance from the viewer,⁠¹⁵⁠It is striking that, with a completely different take on Truchet’s tilings, [⁠16⁠ C. S. Smith and P. Boucher, The tiling patterns of Sebastien Truchet and the topology of structural hierarchy. Leonardo 20, 373–385 (1987) ] also stresses the differences in perception depending on distance from the motif or the scale at which it is viewed. provoking amazing visual effects as in the paintings displayed in Figure ⁠12⁠, where the complex juxtapositions of colors puzzle and draw the eye in, and can even, in full size, make us doubt the reality of what we are actually looking at.

Combining colors. The basic rule is to choose two main colors, red and green for example, which complement each other well, and assign one to the white areas created by the paving, and the other to the black areas. However, in the world of painting, things are not all black and white, and different combinations of the two colors can replace either one or the other for a given area, obtained either by mixing them in varying proportions, or by superimposing one on the other. The choice of one variant or another may be guided, for example, by the shapes that appear and whether or not the artist wishes to emphasize them, or simply by the color harmony of the painting.

Then, during the slow, delicate work of filling in the areas, the artist gives free rein to his inspiration to introduce a third, warmer color here, a cooler one there, as the overall picture takes shape in his mind, and he senses whether or not to broaden his palette. In the end, there are no real rules when it comes to the colors: the constraint of the paving patterns is the framework within which the artist’s freedom to choose, arrange and interact with them can fully expand. In his words:

Coming across a picture of the Ulam spiral in a completely different context, I saw the potential. The creation of the paintings at first depends largely on these calculations, but in the elaboration, the eye and intuition also come into play.

Precision. Long an adept of fast painting, where brushstrokes amalgamate colors into rich, vibrant textures with slightly blurred outlines, Reg Alcorn adopted a different way of painting for the Transitions series: slow, precise work, very sharp contours, which he had previously experimented with in geometrically patterned canvases inspired in particular by Penrose tilings.

Although the colors are well delineated on the canvas, predicting the effect their juxtaposition will produce in the patterns created by the sequence of Truchet tiles is a challenge that only the artist’s long experience and sense of color can meet. And there are surprising outcomes in certain cases, when the colors “vibrate” in contact with each other, whenever the eye is at the right distance from the canvas. All this is the fruit of long-term research, as he explains:

I spent a long time trying to develop a formal grammar capable of exploiting these combinations, in order to create compelling yet legible configurations for any harmony, and to highlight the colors’ distinct identities.

Pigments. Note that the chemical composition of the pigments is very important for this work: for example, the red-green sector shows significant variations in visual impact depending on whether, for example, cadmium red dark is used in combination with phthalocyanine green, or iron oxide red with green earth.

There are actually a dozen top-of-the-range reds, according to paint manufacturers, made of either mineral, vegetable or synthetic pigments, with differences in hue, transparency or opacity. Their texture depends on the thickness of the paint, the additives and tools used, the texture of the canvas fabric and its preparation for the color. Let us take two colors as examples: cadmium red light, an opaque, vivid color with great visual impact, and alizarin crimson red, a transparent, very dark color with a violet-red tendency. Their juxtaposition enhances their identities, while their overlay modifies both colors.

The paintings in the “Transitions” series invite us to discover a chromatic perspective, giving the illusion that colors are at different distances. Composing these paintings, I embarked on an exciting odyssey, exploiting the alchemy of colors and multiple combinations without being committed to representativeness. This is the heart of “Transitions.”

3.3 Variations

The rule we have described for determining the paintings’ motifs, that is, the choice of a sequence of Truchet tiles wound into a spiral, has also been subject to exceptions, even transgressions, in the course of the very many canvases that have been created. These have often proved to be judicious and enriching in terms of new perspectives. Some paintings, for example, are constructed from several spirals starting from different foci, which can give the impression of a more realistic painting: with five foci, one thinks almost instinctively of the more or less symmetrical five-pointed shapes so familiar in the natural environment, like that of a silhouette with a head, two arms and two legs, somehow blurred by the pictorial process, unless the colors chosen by the painter make it appear.

In other paintings, Truchet tiles are replaced by “Pythagorean” rectangles cut diagonally into two triangles of sides $3,4,5$, wound into a spiral in the same way as before. The first consequence is that the canvases are no longer necessarily square, which was almost always the case before, as a matter of construction; the second is that the lines delimiting the spiral are less blended into the overall motif, revealing more of the painting’s structure. Finally, the elongated triangles give rise to smoother, more fluid shapes than Truchet’s tiles. Of course, the artist also played with mixing “Greek” tiles with Truchet’s, or even with squares cut into four triangles along the diagonals – there are countless combination possibilities… An example is shown in Figure ⁠13⁠.

3.4 From so simple a beginning

A stunning characteristic of Reg Alcorn’s process is that, despite its great simplicity, it produces extraordinarily rich and complex patterns. Music is another artistic field where this principle is frequently found.

Electronic musician Grand Ciel experimented with it, notably by mixing loops of very simple sounds of different lengths (on three, four and five beats, for example), on the occasion of a conference-performance organized by the IREM de Limoges for the Fête de la Science 2019, at the Musée national Adrien Dubouché in Limoges, as part of the Year of Mathematics. This show entitled From so simple a beginning sought to dramatize that principle, with a live performance by the painter and musician improvising together, following a two-part lecture by the first author and his colleague Olivier Prot, to introduce the theme, the Ulam spiral and Reg Alcorn’s method.

During a second, longer performance of the show, we also proposed an example of a mathematical question in which complexity appears unexpectedly in a problem that is easy to state, in this case the Jacobsthal function that associates with any integer $n$ the largest difference between two consecutive integers prime to $n$, and for which only about sixty terms are known when applied to primorials.⁠¹⁶⁠https://oeis.org/A048670 The firsts are

and the following is not 38 but 40!

The show’s title quotes Charles Darwin [⁠6⁠ C. Darwin, On the origin of species by means of natural selection, or the preservation of favoured races in the struggle for life. John Murray, London (1859) ], to reflect the fact that the mentioned characteristic, far from applying only to the arts or mathematics, is intrinsic to the evolution of life:

From so simple a beginning, endless forms most beautiful and most wonderful have been, and are being, evolved.

Acknowledgements. The authors are very grateful to the article’s anonymous referees for their careful reading and many helpful suggestions. They also thank Jean-Bernard Bru and Miriam Gellrich Pedra for managing the translation of the original text into English. Special thanks to the Basque Center for Applied Mathematics for funding the translation from French to English. The Magazine of the EMS thanks La Gazette de la Société Mathématique de France for the authorization to republish this English translation of the paper entitled “Les mathématiques vues par un artiste: des objets mathématiques qui inspirent” and published in La Gazette 181 (July 2024).

Stéphane Vinatier is a Professor in Mathematics at the University of Limoges, France. His research is conducted within the XLIM research institute, UMR CNRS 7252. Specialized in algebraic number theory, focusing on the Galois action on invariants in number field extensions under specific ramification conditions. He is also interested in other mathematical domains, such as combinatorics. He has contributed to the French network of research institutes in mathematics education, serving as its head for two years. He continues to engage in experimental education projects. stephane.vinatier@unilim.fr William Reginald Alcorn was born in Zambia in 1950 to Irish and Scottish parents. He developed a passion for painting at a very early age. After studying humanities in England, he traveled around Europe, eventually settling in France. With projects in music, languages, science and, more recently, mathematics, he divides his time between his painting studio and popularizing the arts, notably as part of the activities of the IREM of Limoges. regalcorn.frescoevent@gmail.com

1. ¹

   https://www.reg-alcorn.fr

2. ²

   Institute of Research on Mathematics Education.

3. ³

   Center for Scientific, Technical and Industrial Culture.

4. ⁴

   That is why Reg Alcorn is listed as author of this article, almost entirely written by the first author and based essentially on the artistic investigation of the second.

5. ⁵

   Johannes Kepler, German astronomer (1571–1630).

6. ⁶

   See [⁠16⁠ C. S. Smith and P. Boucher, The tiling patterns of Sebastien Truchet and the topology of structural hierarchy. Leonardo 20, 373–385 (1987) , p. 384, note 5.] for a discussion of these reductions.

7. ⁷

   https://jacques-andre.fr/faqtypo/truchet/

8. ⁸

   https://encyclopedie.uchicago.edu

9. ⁹

   https://enccre.academie-sciences.fr/encyclopedie/

10. ¹⁰

    The plates date from 1705, but this encyclopedia only began to be published in fascicules from 1761 onwards.

11. ¹¹

    American writer (1914–2010), great popularizer of mathematics.

12. ¹²

    Or rather except two!

13. ¹³

    The current record is for $k=27$, set by Gahan in 2019, see https://oeis.org/A327760.

14. ¹⁴

    Although he might occasionally deviate from it, over the course of the two hundred paintings in this series.

15. ¹⁵

    It is striking that, with a completely different take on Truchet’s tilings, [⁠16⁠ C. S. Smith and P. Boucher, The tiling patterns of Sebastien Truchet and the topology of structural hierarchy. Leonardo 20, 373–385 (1987) ] also stresses the differences in perception depending on distance from the motif or the scale at which it is viewed.

16. ¹⁶

    https://oeis.org/A048670

References

1. J. André, De Pacioli à Truchet: trois siècles de géométrie pour les caractères. In 4000 ans d’histoire des mathématiques: les mathématiques dans la longue durée. IREM de Rennes, Rennes, France (2002) https://bibnum.publimath.fr/IWH/IWH02004.pdf
2. J. André, Les planches de pavages de Truchet. (2010)https://jacques-andre.fr/faqtypo/truchet/truchet-planches.pdf
3. J. André and D. Girou, Father Truchet, the typographic point, the Romain du roi, and tilings. TUGboat 20, 8–14 (1999)https://www.tug.org/TUGboat/Articles/tb20-1/tb62andr.pdf
4. H. Cohen, High precision computations of Hardy–Littlewood constants. Preprint, (1998) https://oeis.org/A221712/a221712.pdf
5. K. Conrad, Hardy–Littlewood constants. In Mathematical properties of sequences and other combinatorial structures (Los Angeles, CA, 2002), pp. 133–154, Kluwer Acad. Publ., Boston, MA (2003)
6. C. Darwin, On the origin of species by means of natural selection, or the preservation of favoured races in the struggle for life. John Murray, London (1859)
7. D. Diderot, Carreau s. m. (Architecture). In Encyclopédie ou dictionnaire raisonné des sciences, des arts et des métiers. Vol. II., pp. 699–701, Briasson, Paris (1752) https://gallica.bnf.fr/ark:/12148/bpt6k50534p/f705
8. D. Doüat, Méthode pour faire une infinité de desseins différens, avec des carreaux mi-partis de deux couleurs par une ligne diagonale. Jacques Quillau, Imprimeur Juré de l’Université, Paris (1722) https://gallica.bnf.fr/ark:/12148/bpt6k5823204r
9. F. Dress and M. Olivier, Polynômes prenant des valeurs premières. Experiment. Math. 8, 319–338 (1999)
10. P. Esperet and D. Girou, Coloriage du pavage dit ‘de Truchet.’ Cahiers GUTenberg 31, 5–18 (1998) http://www.numdam.org/item/CG_1998___31_5_0/
11. M. Gardner, Mathematical games: The remarkable lore of the prime numbers. Scientific American 210.3 120–130 (1964)
12. B. Green and T. Tao, The primes contain arbitrarily long arithmetic progressions. Ann. of Math. (2) 167, 481–547 (2008)
13. M. J. Jacobson, Jr. and H. C. Williams, New quadratic polynomials with high densities of prime values. Math. Comp. 72, 499–519 (2003)
14. S. Marquès and S. Vinatier, Alignments in Ulam’s spiral. (Work in progress) (2025)
15. L. Rougetet and M. Boutin, Jeu de parquet et combinaisons, ou la double patrimonialisation d’un objet et de ses savoirs mathématiques. Philos. Sci. (Paris) 26, 91–121 (2022)
16. C. S. Smith and P. Boucher, The tiling patterns of Sebastien Truchet and the topology of structural hierarchy. Leonardo 20, 373–385 (1987)
17. M. L. Stein, S. M. Ulam and M. B. Wells, A visual display of some properties of the distribution of primes. Amer. Math. Monthly 71, 516–520 (1964)
18. S. Truchet, Mémoire sur les combinaisons. In Mémoires de mathématique et de physique tirés des registres de l’Académie Royale des Sciences, pp. 363–372, Paris (1704) https://gallica.bnf.fr/ark:/12148/bpt6k3486m/f517
19. S. Vinatier and R. Alcorn, Les maths vues par un artiste: une expérience de diffusion de la culture mathématique via l’art et l’histoire de l’art. Gaz. Math. 144 48–53 (2015)