The circular restricted three-body problem: a modern symplectic viewpoint

Agustin Moreno

doi:10.4171/mag/227

We give an overview of recent advances on the circular restricted three-body problem, from the perspective of modern symplectic geometry, and describe a “symplectic toolkit” created in connection to spacecraft trajectory design. This is based on the author’s recent book draft.

1 Introduction

The three-body problem is the dynamical system corresponding to three masses under gravitational interaction, as described by Newton’s law. It is one of those ancient conundrums that has withstood the ages, maturing like a complex wine. Its study goes back at least to the times of Newton, and its history is tied up with some of the most brilliant scientific figures, like Kepler, Poincaré, Arnold, Moser, and so many others, who had the courage to try to delve into its well-hidden secrets. The aim of this short note is to describe some of the recent advances in a special case of this problem, made possible through the modern methods of symplectic geometry. In what follows, we will restrict our attention to the circular and restricted three-body problem (or CR3BP for short), corresponding to the case where one of the masses is negligible, and the other two move in circles around their common center of mass. We will focus on the spatial problem, where the negligible mass moves in three-space, as opposed to the planar problem, where it moves in the plane. Despite the simplifications and approximations, this is still an outstanding open challenge.

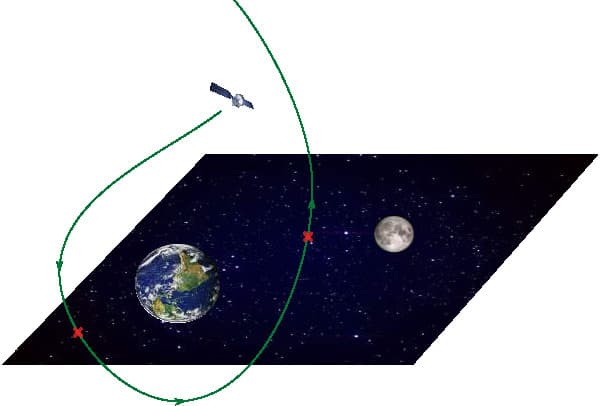
The CR3BP is not only interesting from a theoretical point of view, but also from a practical perspective, due to its deep connections to astronomy and space exploration. Namely, the CR3BP is one of the most basic models approximating the motion of a spacecraft under the influence of a planet–moon system. This is a modern interpretation: unlike the times of Newton, when space travel was but a wild opium dream, in the current day and age, when mission proposals to remote regions of our expanding Universe are common currency, the CR3BP is one of the preeminent models used for spacecraft trajectory design. In the context of astrodynamics, the CR3BP is then the theoretical starting point supporting the high-fidelity (or ephemeris) numerical studies which go into actual mission proposals. While finding trajectories that meet the requirements of an actual mission is a very complicated art, the families of periodic orbits found in the CR3BP, as well as the stable/unstable manifolds of some of them, can be used as building blocks for designing the desired trajectories, and to transfer between them.

We will first discuss some of the theoretical aspects, and then those aspects which are closer to applications. In particular, we will describe a “symplectic toolkit” created with the needs of trajectory design in mind, the result of a collaboration of the author with NASA engineers. More details can be found in the author’s recent book draft [⁠13⁠ A. Moreno, The symplectic geometry of the three-body problem. arXiv:2101.04438v3 ([v1] 2021, [v3] 2024) ] (see also Quanta Magazine’s recent article [⁠19⁠ L. Sloman, Geometers engineer new tools to wrangle spacecraft orbits. Quanta Magazine (2024) https://www.quantamagazine.org/geometers-engineer-new-tools-to-wrangle-spacecraft-orbits-20240415]).

2 The CR3BP

We consider three bodies: Earth (E), the Moon (M) and a satellite (S), with masses $m_{E}$ , $m_{M}$ , and $m_{S}$ . One has the following cases and assumptions:

(Restricted case) $m_{S} = 0$ , i.e., the satellite is negligibly small when compared with the primaries E and M;
(Circular assumption) Each primary moves in a circle, centered around the common center of mass of the two (as opposed to general ellipses);
(Planar case) S moves in the ecliptic plane containing the primaries;
(Spatial case) The planar assumption is dropped, and S is allowed to move in three-dimensional space.

We denote the mass ratio by $μ = \frac{m _{M}}{m _{E} + m _{M}} \in [0, 1],$ and we normalize so that $m_{E} + m_{M} = 1$ , and so $μ = m_{M}$ can be thought of as the mass of the Moon. In rotating coordinates, in which both primaries are at rest, the Hamiltonian describing the problem is actually autonomous. If the positions of the Earth and the Moon are $E = (μ, 0, 0)$ and $M = (- 1 + μ, 0, 0)$ , the Hamiltonian is

H : R^{3} \ {E, M} \times R^{3} \to R,

H (q, p) = \frac{1}{2} ∥ p ∥^{2} - \frac{μ}{∥ q - M ∥} - \frac{1 - μ}{∥ q - E ∥} + p_{1} q_{2} - p_{2} q_{1} .

By conservation of energy, this means that $H$ is a preserved quantity of the Hamiltonian motion. The planar problem is the subset ${p_{3} = q_{3} = 0},$ which is clearly invariant under the Hamiltonian dynamics. The two parameters in the problem are the Jacobi constant $c$ (the energy value), and $μ$ .

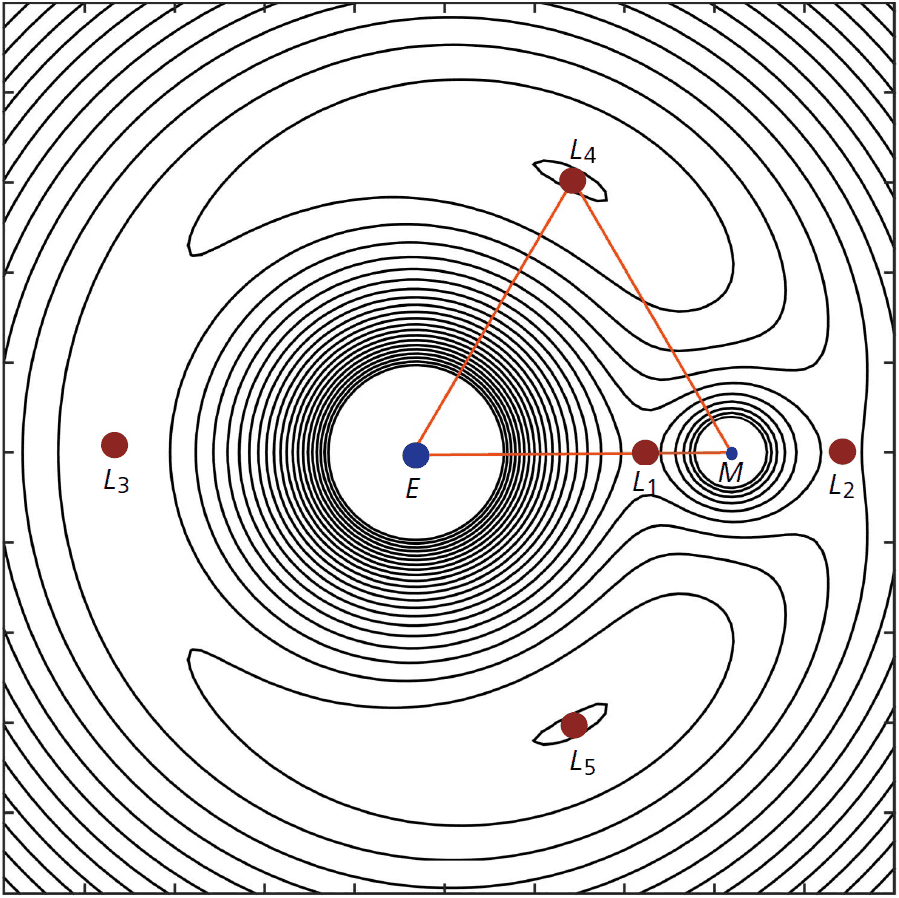
As computed by Euler and Lagrange, there are precisely five critical points of $H$ , called the Lagrangian points $L_{i} = L_{i} (μ),$ $i = 1, \dots, 5$ , ordered so that $H (L_{1}) < H (L_{2}) < H (L_{3}) < H (L_{4}) = H (L_{5})$ . The low-energy range corresponds to $c < H (L_{1})$ (or slightly above).

For $c \in R$ , consider the energy hypersurface $Σ_{c} = H^{- 1} (c)$ . If

π : R^{3} \ {E, M} \times R^{3} \to R^{3} \ {E, M}, π (q, p) = q,

is the projection onto the position coordinate, we define the Hill region of energy $c$ as

K_{c} = π (Σ_{c}) \in R^{3} \ {E, M} .

This is the region in space where the satellite of energy $c$ is allowed to move. If $c < H (L_{1})$ , then $K_{c}$ has three connected components: a bounded one around the Earth, another bounded one around the Moon, and an unbounded one. Denote the first two components by $K_{c}^{E}$ and $K_{c}^{M}$ , and set $Σ_{c}^{E} = π^{- 1} (K_{c}^{E}) \cap Σ_{c}$ , $Σ_{c}^{M} = π^{- 1} (K_{c}^{M}) \cap Σ_{c}$ . As $c$ crosses the value $H (L_{1})$ , $K_{c}^{E}$ and $K_{c}^{M}$ get glued together into a new connected component, $K_{c}^{E, M}$ , topologically their connected sum. Then, the satellite in principle has enough energy to transfer between Earth and the Moon. See Figure ⁠1⁠.

*Figure 1.* The Hill regions and the Lagrange points for the planar problem. 🅭🅯 CC BY 4.0

3 Theoretical aspects

3.1 The Poincaré–Birkhoff theorem, and the planar CR3BP

Poincaré [⁠16⁠ H. Poincaré, Les méthodes nouvelles de la mécanique céleste. Tome I. Les Grands Classiques Gauthier-Villars, Paris (1892); reprint: Les Grands Classiques Gauthier-Villars, Lib. Sci. Tech. Albert Blanchard, Paris (1987) , ⁠17⁠ H. Poincaré, Sur un théorème de géométrie. Rend. Circ. Mat. Palermo 33, 375–407 (1912) ] reduced the problem of finding periodic orbits in the planar CR3BP to:

finding a global surface of section for the dynamics;
proving a fixed point theorem for the resulting first-return map.

This is the setting for the celebrated Poincaré–Birkhoff theorem.

3.2 Collision regularization

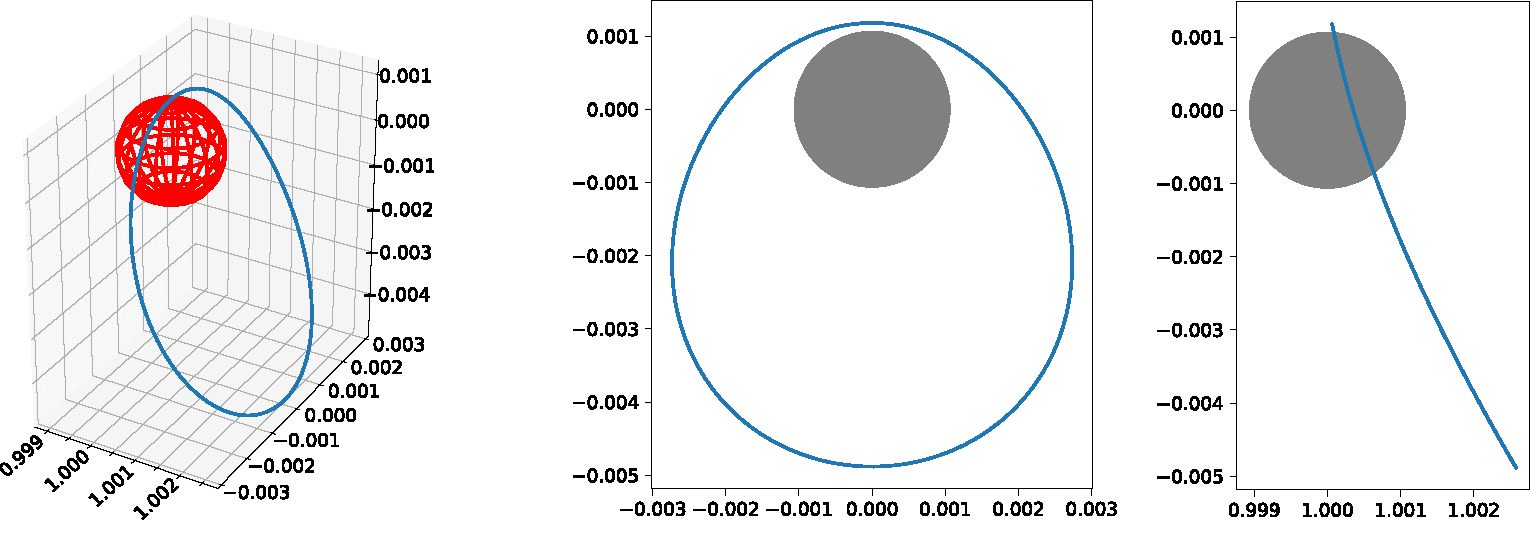
The $5$ -dimensional energy hypersurfaces in the spatial CR3BP are non-compact, due to collisions of the massless body $S$ with one of the primaries. Two-body collisions can be regularized via Moser’s recipe. The bounded components $Σ_{c}^{E}$ and $Σ_{c}^{M}$ (for $c < H (L_{1})$ ), as well as $Σ_{c}^{E, M}$ (for $c \in (H (L_{1}), H (L_{1}) + ε)$ ), are thus compactified to compact manifolds $\overline{Σ}_{c}^{E} ≅ \overline{Σ}_{c}^{M} ≅ S^{3} \times S^{2}$ , and $\overline{Σ}_{c}^{E, M} ≅ S^{2} \times S^{3} # S^{2} \times S^{3}$ . In the planar problem, we obtain copies of $R P^{3}$ and $R P^{3} # R P^{3}$ . We use the notation $\overline{Σ}_{P, c}^{E}$ , $\overline{Σ}_{P, c}^{M}$ and $\overline{Σ}_{P, c}^{E, M}$ for the corresponding planar regularized energy level sets.

3.3 The advent of contact geometry in the CR3BP

It was only recently that the modern techniques from contact and symplectic geometry (holomorphic curves, Floer theory, etc.) have been made to bear on the CR3BP. This is due to the following result.

Theorem 1 ([] (planar problem), [] (spatial problem)).

If $c < H (L_{1})$ , the regularized hypersurfaces $\overline{Σ}_{c}^{E}, \overline{Σ}_{c}^{M}, \overline{Σ}_{P, c}^{E}, \overline{Σ}_{P, c}^{M}$ carry contact structures. The same holds for $\overline{Σ}_{c}^{E, M}$ and $\overline{Σ}_{P, c}^{E, M}$ , if $c \in (H (L_{1}), H (L_{1}) + ε)$ for sufficiently small $ε > 0$ .

3.4 Open book decompositions

We have the following fundamental notion from smooth topology.

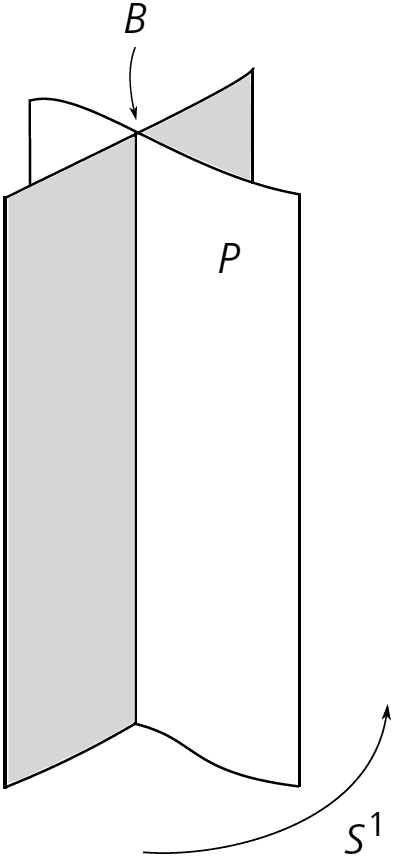
Definition 3.1 (Open book decomposition). Let $M$ be a closed manifold. A (concrete) open book decomposition on $M$ is a fibration $π : M \ B \to S^{1}$ , where $B \subset M$ is a closed, codimension- $2$ submanifold with trivial normal bundle. We further assume that $π (b, r, θ) = θ$ along some collar neighborhood $B \times D^{2} \subset M$ , where $(r, θ)$ are polar coordinates on the disk factor.

The submanifold $B$ is called the binding, and the closures of the fibers $P = P_{θ} = \overline{π^{- 1}} (θ)$ are called the pages, which satisfy $\partial P_{θ} = B$ for every $θ$ . We usually denote a concrete open book by the pair $(π, B)$ , but also use the abstract notation $M = OB (P, φ)$ , where $φ$ is a diffeomorphism $φ : P \to P$ with $φ = i d$ near $B$ (the monodromy). See Figure ⁠2⁠.

*Figure 2.* A neighborhood of the binding look precisely like the pages of an open book, whose front cover has been glued to its back cover via some gluing map (the monodromy). 🅭🅯 CC BY 4.0

If $M$ is oriented and endowed with an open book decomposition, then the natural orientation on the circle induces orientations on the pages, which in turn induce the boundary orientation on the binding.

Definition 3.2 (Giroux). Let $(M, ξ)$ be an oriented contact manifold, and $(π, B)$ an open book decomposition on $M$ . Then $ξ$ is supported by the open book if one can find a positive contact form $α$ for $ξ$ (called a Giroux form) such that:

(i) $α_{B} := α ∣_{B}$ is a positive contact form for $B$ ;

(ii) $d α ∣_{P}$ is a positive symplectic form on the interior of every page $P$ .

Here, a positive contact form is a contact form $α$ on $M^{2 n - 1}$ such that the orientation induced by the volume form $α \land d α^{n - 1}$ coincides with the given orientation on $M$ .

We say that the open book is adapted to the dynamics of $α$ if ⁠(i)⁠ and ⁠(ii)⁠ hold. One has the following fundamental result.

Theorem 2 (Giroux []).

Every open book decomposition supports a unique isotopy class of contact structures. Any contact structure admits a supporting open book decomposition.

Here, two contact structures are said to be isotopic if they can be joined by a smooth path $ξ_{t}$ of contact structures. By Gray’s stability result, isotopic contact structures are contactomorphic, i.e., there exists a diffeomorphism which carries one to the other.

Remark 3.3. In fact, Giroux’s result is stronger, as there is in fact a correspondence between contact structures up to isotopy and open books up to a notion of positive stabilization. Giroux proved this in dimension $3$ , and the result was recently established in higher dimensions by Breen, Honda, and Huang [⁠3⁠ J. Breen, K. Honda and Y. Huang, The Giroux correspondence in arbitrary dimensions. arXiv:2307.02317v2 ([v1] 2023, [v2] 2024) ].

We usually write $(M, ξ) = OB (P, φ)$ to indicate that the contact structure $ξ$ is supported by the open book $(P, φ)$ .

The Giroux correspondence reduces the topological study of contact manifolds to the topological study of open books. However, this result holds only when the (isotopy class of the) contact structure is fixed, and the contact form (and hence the dynamics) is auxiliary; Giroux’s result is not dynamical, but rather topological/geometrical. But this will serve as motivation for what comes next.

3.5 Open books in the CR3BP

Let $\overline{Σ}_{c}$ stand for either $\overline{Σ}_{c}^{E}$ , $\overline{Σ}_{c}^{M}$ or $\overline{Σ}_{c}^{E, M}$ (for the spatial problem). The following result generalizes the approach of Poincaré in the planar problem (i.e., step ⁠(1)⁠) to the spatial problem. Combining Theorem ⁠1⁠ with the Giroux correspondence, we know there exist supporting open book decompositions on $\overline{Σ}_{c}$ when $c$ belongs to the low-energy range. However, as we emphasized already, this correspondence does not give adapted open books whenever the dynamics is fixed. The content of the following result is that the given dynamics of the spatial CR3BP in the low-energy range, and near the primaries, is given by a contact form which is a Giroux form for some concrete open book.

Theorem 3 (Moreno–van Koert []).

For any $μ \in [0, 1]$ , if $c$ lies in the low-energy range, $\overline{Σ}_{c}$ admits a supporting open book decomposition for energies $c < H (L_{1})$ that is adapted to the dynamics. Furthermore, if $μ < 1$ , then there is $ε > 0$ such that the same holds for $c \in (H (L_{1}), H (L_{1}) + ε)$ . The open books have the following abstract form:

\overline{Σ}_{c} ≅ ⎩ ⎨ ⎧ (S^{*} S^{3}, ξ_{std}) = OB (D^{*} S^{2}, τ^{2}), (S^{*} S^{3}, ξ_{std}) # (S^{*} S^{3}, ξ_{std}) = OB (D^{*} S^{2} ♮ D^{*} S^{2}, τ_{1}^{2} \circ τ_{2}^{2}), if c < H (L_{1}), if c \in (H (L_{1}), H (L_{1}) + ε), i f μ < 1.

In all cases, the binding is the planar problem is

B = \overline{Σ}_{P, c} = ⎩ ⎨ ⎧ (S^{*} S^{2}, ξ_{std}), (S^{*} S^{2}, ξ_{std}) # (S^{*} S^{2}, ξ_{std}), if c < H (L_{1}) if c \in (H (L_{1}), H (L_{1}) + ε), i f μ < 1.

Here, $D^{*} S^{2}$ is the unit cotangent bundle of the $2$ -sphere, $τ$ is the positive Dehn–Seidel twist, and $D^{*} S^{2} ♮ D^{*} S^{2}$ denotes the boundary connected sum of two copies of $D^{*} S^{2}$ . The monodromy of the second open book is the composition of the square of the positive Dehn–Seidel twists along both zero sections (they commute).

*Figure 3.* Theorem ⁠3⁠ admits a physical interpretation: away from collisions, the orbits of the negligible mass point intersect the plane containing the primaries transversely. The “pages” ${q_{3} = 0, p_{3} > 0}$ , ${q_{3} = 0, p_{3} < 0}$ of the “physical” open book $(q, p) \mapsto \frac{q _{3} + i p _{3}}{∥ q _{3} + i p _{3} ∥} \in S^{1}$ , are global hypersurfaces of section outside of the collision locus. 🅭🅯 CC BY 4.0

4 Practical aspects

A given Hamiltonian system usually depends on parameters (e.g., energy or mass parameters), which one may vary. Under such deformations, periodic orbits may undergo bifurcation, a mechanism by which new families of periodic trajectories arise. The way different families can connect to each other is encoded in the topology of a bifurcation graph. The aim of this chapter is then to introduce a “symplectic toolkit,” extracted from the modern methods of symplectic geometry, and designed to systematically map out how different orbit families merge together.

4.1 Symplectic data analysis

The “symplectic toolkit” consists of the following elements:

Floer numbers: Integers that are invariant under bifurcation, and so can help predict the existence of orbits.
The $B$ -signs [⁠7⁠ U. Frauenfelder and A. Moreno, On GIT quotients of the symplectic group, stability and bifurcations of periodic orbits (with a view towards practical applications). J. Symplectic Geom. 21, 723–773 (2023) ]: a $\pm$ sign associated to each elliptic or hyperbolic orbits, which helps predict bifurcations, and generalizes the classical Krein theory [⁠9⁠ M. G. Kreĭn, On the application of an algebraic proposition in the theory of matrices of monodromy. Uspehi Matem. Nauk (N.S.) 6, 171–177 (1951) , ⁠10⁠ M. G. Kreĭn, On the theory of entire matrix functions of exponential type. Ukrain. Mat. Žurnal 3, 164–173 (1951) ].
Global topological methods: the (geometric invariant theory) GIT-sequence [⁠7⁠ U. Frauenfelder and A. Moreno, On GIT quotients of the symplectic group, stability and bifurcations of periodic orbits (with a view towards practical applications). J. Symplectic Geom. 21, 723–773 (2023) ], a sequence of spaces whose global topology encodes bifurcations, and refines Broucke’s stability diagram [⁠4⁠ R. Broucke, Stability of periodic orbits in the elliptic, restricted three-body problem. AIAA J. 7, 1003–1009 (1969) ] by adding the $B$ -signs.
CZ-index [⁠6⁠ C. Conley and E. Zehnder, Morse-type index theory for flows and periodic solutions for Hamiltonian equations. Comm. Pure Appl. Math. 37, 207–253 (1984) , ⁠18⁠ J. Robbin and D. Salamon, The Maslov index for paths. Topology 32, 827–844 (1993) ]: a winding number associated to non-degenerate orbits, extracted from the topology of the symplectic group. It can be used to determine which families connect to which.

4.2 Numerical work

We now describe some numerical work where we put the symplectic toolkit into practical use. This is based on the article [⁠14⁠ A. Moreno, C. Aydin, O. van Koert, U. Frauenfelder and D. Koh, Bifurcation graphs for the CR3BP via symplectic methods: On the Jupiter–Europa and Saturn–Enceladus systems. J. Astronaut. Sci. 71, article no. 51 (2024) ].

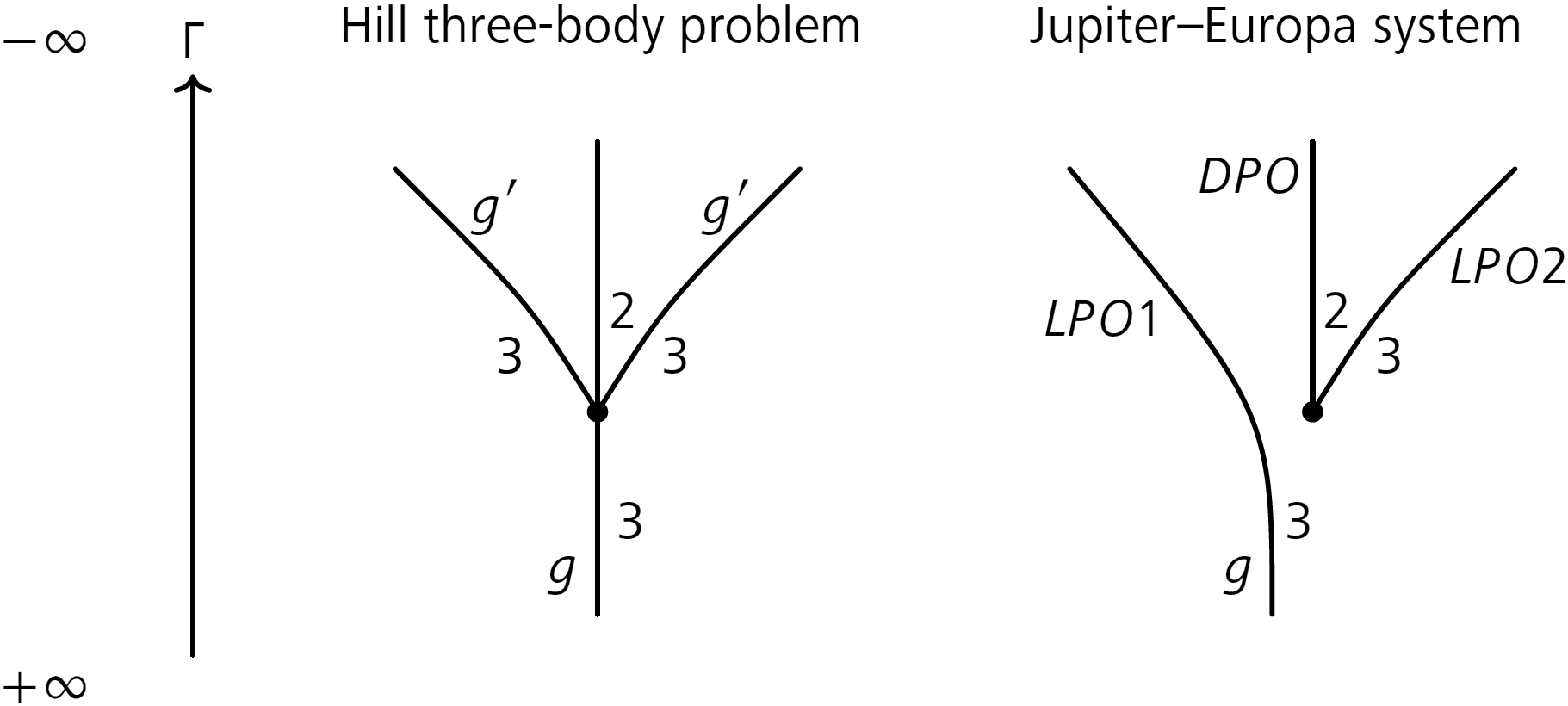
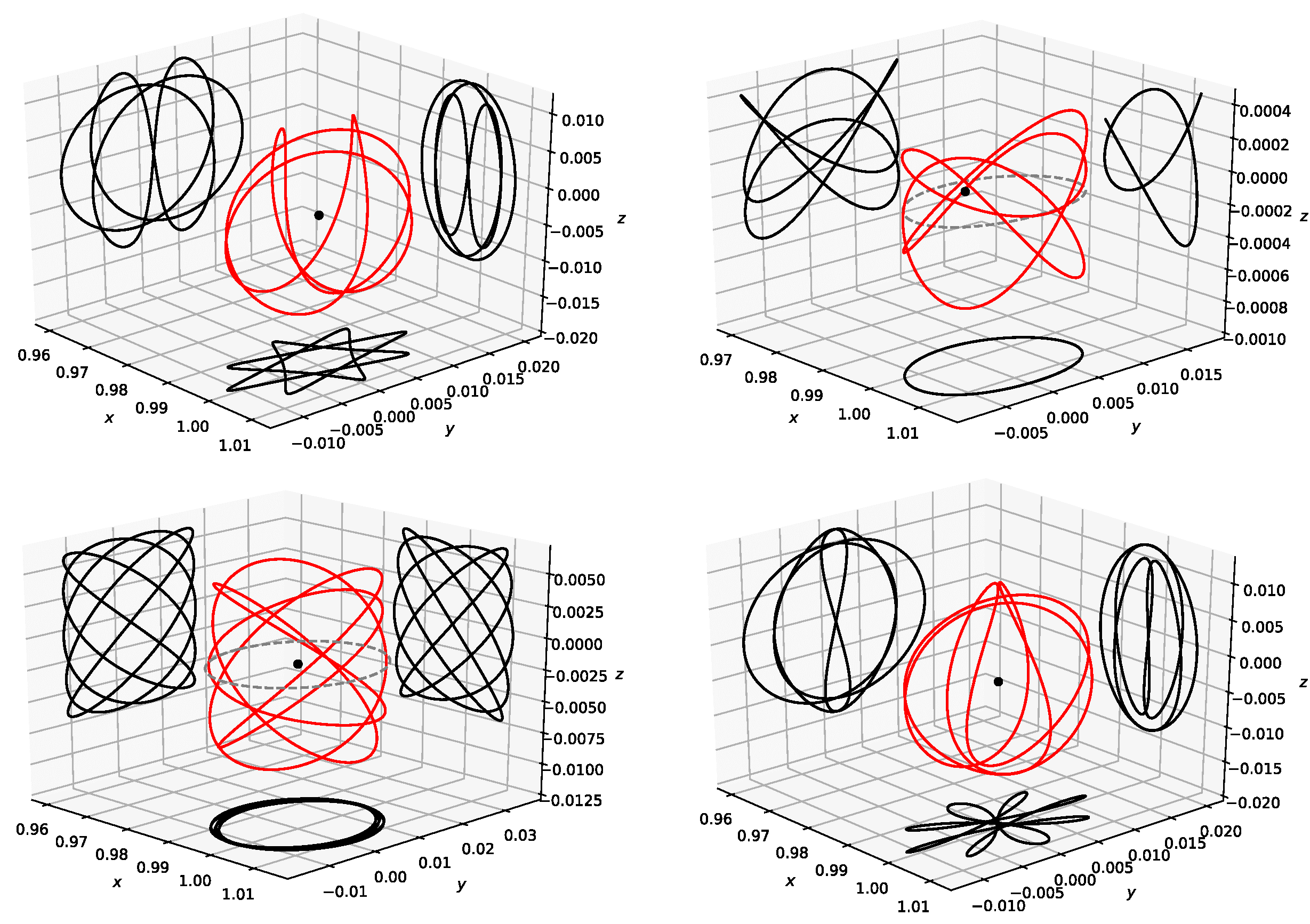
We consider the Jupiter–Europa system (JE), which corresponds to a CR3BP with $μ = 2.5266448850435 e^{- 05}$ , and the Saturn–Enceladus system (SE), $μ = 1.9002485658670 e^{- 07}$ . These two systems are of tremendous current interest for space agencies such as NASA, as they may have conditions suitable for real life problems. Starting from the Hill 3BP, we deform to JE and to SE. One symmetry is broken, and families behave more generically. In what follows, we use $Γ = - 2 c$ .

4.3 Planar direct/prograde orbits

The planar pitchfork bifurcation described by Hénon [⁠12⁠ H. Michel, Numerical exploration of the restricted problem. V. Hill’s case: Periodic orbits and their stability. Astron. Astrophys. 1, 223–238 (1969) ] in the Hill 3BP (concerning planar orbit families $f, g, g^{'}$ ) becomes a generic broken bifurcation in the planar JE CR3BP, see Figure ⁠4⁠.

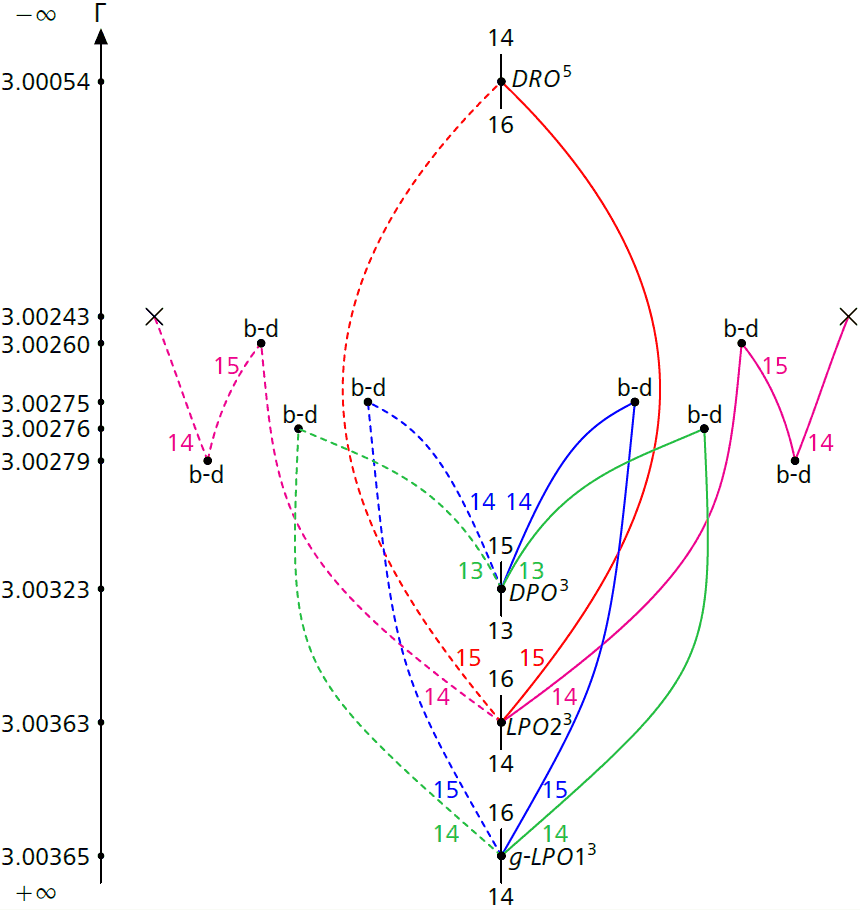
*Figure 4.* Bifurcations of planar direct/prograde orbits with corresponding CZ-index. 🅭🅯 CC BY 4.0

4.4 Spatial bifurcation graphs between planar prograde and retrograde orbits

A bifurcation graph relating third covers of the direct orbits $g, g^{'}$ , and fifth covers of planar retrograde orbits $f$ , connected via spatial families, was obtained by Aydin [⁠2⁠ C. Aydin, From Babylonian lunar observations to Floquet multipliers and Conley–Zehnder indices. J. Math. Phys. 64, article no. 082902 (2023) ]. We deformed it to JE in Figure ⁠5⁠.

*Figure 5.* Bifurcation graph for JE, between $g$ - $L PO 1^{3}$ , $D P O^{3}$ , $L PO 2^{3}$ , and $D R O^{5}$ . 🅭🅯 CC BY 4.0

*Figure 6.* Prograde to retrograde spatial connection, red CZ-index 15 in Figure ⁠5⁠. 🅭🅯 CC BY 4.0

4.5 Halo orbits in SE

We consider halo orbits coming out of the Lagrange point $L_{2}$ in SE. This family appears also in NASA’s technical report on the Enceladus Orbilander [⁠11⁠ S. M. MacKenzie, K. W. Kirby and P. J. Greenauer, Enceladus Orbilander: A flagship mission concept for astrobiology. Tech. rep. 20205008712, The Johns Hopkins Applied Physics Laboratory and NASA (2020) https://ntrs.nasa.gov/citations/20205008712], and is meant to be used to visit the poles in future missions. The corresponding family for the Earth–Moon system is currently very popular, as it will be where NASA’s Gateway Space Station will be parked. The most interesting part of the family in SE occurs just after the CZ-index jumps from 3 to 4, where orbits are stable and close to the water plumes.

*Figure 7.* Halo-polar orbit ( $Γ = 3.000034709155895$ ) with an altitude of 29 km. The CZ-index has just jumped to 4, and is doubly elliptic. 🅭🅯 CC BY 4.0

Agustin Moreno is a junior professor in the Department of Mathematics at Heidelberg University in Germany, as well as a former member of the School of Mathematics at the Institute for Advanced Study, Princeton. He holds degrees from the University of Cambridge, and from the Humboldt University in Berlin, where he finished his PhD (started at the University College London, UK). He has been affiliated with the Berlin Mathematical School, and has been a research fellow at the Mittag-Leffler Institute in Sweden – an institution famously tied to the work of Poincaré on the three-body problem – where much of his work on the very same problem was carried out. Agustin Moreno’s research lies at the crossroads of geometry, topology, dynamics and mathematical physics, with further interest in applications to space mission design, which he pursues in collaboration with navigational engineers at NASA and aerospace engineers at the University of Colorado, Boulder, USA. agustin.moreno2191@gmail.com

References

P. Albers, U. Frauenfelder, O. van Koert and G. P. Paternain, Contact geometry of the restricted three-body problem. Comm. Pure Appl. Math. 65, 229–263 (2012)
C. Aydin, From Babylonian lunar observations to Floquet multipliers and Conley–Zehnder indices. J. Math. Phys. 64, article no. 082902 (2023)
J. Breen, K. Honda and Y. Huang, The Giroux correspondence in arbitrary dimensions. arXiv:2307.02317v2 ([v1] 2023, [v2] 2024)
R. Broucke, Stability of periodic orbits in the elliptic, restricted three-body problem. AIAA J. 7, 1003–1009 (1969)
W. Cho, H. Jung and G. Kim, The contact geometry of the spatial circular restricted 3-body problem. Abh. Math. Semin. Univ. Hambg. 90, 161–181 (2020)
C. Conley and E. Zehnder, Morse-type index theory for flows and periodic solutions for Hamiltonian equations. Comm. Pure Appl. Math. 37, 207–253 (1984)
U. Frauenfelder and A. Moreno, On GIT quotients of the symplectic group, stability and bifurcations of periodic orbits (with a view towards practical applications). J. Symplectic Geom. 21, 723–773 (2023)
E. Giroux, Géométrie de contact: de la dimension trois vers les dimensions supérieures. In Proceedings of the International Congress of Mathematicians, Vol. II (Beijing, 2002), Higher Ed. Press, Beijing, 405–414 (2002)
M. G. Kreĭn, On the application of an algebraic proposition in the theory of matrices of monodromy. Uspehi Matem. Nauk (N.S.) 6, 171–177 (1951)
M. G. Kreĭn, On the theory of entire matrix functions of exponential type. Ukrain. Mat. Žurnal 3, 164–173 (1951)
S. M. MacKenzie, K. W. Kirby and P. J. Greenauer, Enceladus Orbilander: A flagship mission concept for astrobiology. Tech. rep. 20205008712, The Johns Hopkins Applied Physics Laboratory and NASA (2020) https://ntrs.nasa.gov/citations/20205008712
H. Michel, Numerical exploration of the restricted problem. V. Hill’s case: Periodic orbits and their stability. Astron. Astrophys. 1, 223–238 (1969)
A. Moreno, The symplectic geometry of the three-body problem. arXiv:2101.04438v3 ([v1] 2021, [v3] 2024)
A. Moreno, C. Aydin, O. van Koert, U. Frauenfelder and D. Koh, Bifurcation graphs for the CR3BP via symplectic methods: On the Jupiter–Europa and Saturn–Enceladus systems. J. Astronaut. Sci. 71, article no. 51 (2024)
A. Moreno and O. van Koert, Global hypersurfaces of section in the spatial restricted three-body problem. Nonlinearity 35, 2920–2970 (2022)
H. Poincaré, Les méthodes nouvelles de la mécanique céleste. Tome I. Les Grands Classiques Gauthier-Villars, Paris (1892); reprint: Les Grands Classiques Gauthier-Villars, Lib. Sci. Tech. Albert Blanchard, Paris (1987)
H. Poincaré, Sur un théorème de géométrie. Rend. Circ. Mat. Palermo 33, 375–407 (1912)
J. Robbin and D. Salamon, The Maslov index for paths. Topology 32, 827–844 (1993)
L. Sloman, Geometers engineer new tools to wrangle spacecraft orbits. Quanta Magazine (2024) https://www.quantamagazine.org/geometers-engineer-new-tools-to-wrangle-spacecraft-orbits-20240415

Cite this article

Agustin Moreno, The circular restricted three-body problem: a modern symplectic viewpoint. Eur. Math. Soc. Mag. 135 (2025), pp. 33–38

DOI 10.4171/MAG/227

🅭🅯

This open access article is published by EMS Press under a CC BY 4.0 license, with the exception of logos and branding of the European Mathematical Society and EMS Press, and where otherwise noted.

Back to Issue 135

[bib-bib1] P. Albers, U. Frauenfelder, O. van Koert and G. P. Paternain, Contact geometry of the restricted three-body problem. Comm. Pure Appl. Math. 65, 229–263 (2012)

[bib-bib2] C. Aydin, From Babylonian lunar observations to Floquet multipliers and Conley–Zehnder indices. J. Math. Phys. 64, article no. 082902 (2023)

[bib-bib3] J. Breen, K. Honda and Y. Huang, The Giroux correspondence in arbitrary dimensions. arXiv:2307.02317v2 ([v1] 2023, [v2] 2024)

[bib-bib4] R. Broucke, Stability of periodic orbits in the elliptic, restricted three-body problem. AIAA J. 7, 1003–1009 (1969)

[bib-bib5] W. Cho, H. Jung and G. Kim, The contact geometry of the spatial circular restricted 3-body problem. Abh. Math. Semin. Univ. Hambg. 90, 161–181 (2020)

[bib-bib6] C. Conley and E. Zehnder, Morse-type index theory for flows and periodic solutions for Hamiltonian equations. Comm. Pure Appl. Math. 37, 207–253 (1984)

[bib-bib7] U. Frauenfelder and A. Moreno, On GIT quotients of the symplectic group, stability and bifurcations of periodic orbits (with a view towards practical applications). J. Symplectic Geom. 21, 723–773 (2023)

[bib-bib8] E. Giroux, Géométrie de contact: de la dimension trois vers les dimensions supérieures. In Proceedings of the International Congress of Mathematicians, Vol. II (Beijing, 2002), Higher Ed. Press, Beijing, 405–414 (2002)

[bib-bib9] M. G. Kreĭn, On the application of an algebraic proposition in the theory of matrices of monodromy. Uspehi Matem. Nauk (N.S.) 6, 171–177 (1951)

[bib-bib10] M. G. Kreĭn, On the theory of entire matrix functions of exponential type. Ukrain. Mat. Žurnal 3, 164–173 (1951)

[bib-bib11] S. M. MacKenzie, K. W. Kirby and P. J. Greenauer, Enceladus Orbilander: A flagship mission concept for astrobiology. Tech. rep. 20205008712, The Johns Hopkins Applied Physics Laboratory and NASA (2020) https://ntrs.nasa.gov/citations/20205008712

[bib-bib12] H. Michel, Numerical exploration of the restricted problem. V. Hill’s case: Periodic orbits and their stability. Astron. Astrophys. 1, 223–238 (1969)

[bib-bib13] A. Moreno, The symplectic geometry of the three-body problem. arXiv:2101.04438v3 ([v1] 2021, [v3] 2024)

[bib-bib14] A. Moreno, C. Aydin, O. van Koert, U. Frauenfelder and D. Koh, Bifurcation graphs for the CR3BP via symplectic methods: On the Jupiter–Europa and Saturn–Enceladus systems. J. Astronaut. Sci. 71, article no. 51 (2024)

[bib-bib15] A. Moreno and O. van Koert, Global hypersurfaces of section in the spatial restricted three-body problem. Nonlinearity 35, 2920–2970 (2022)

[bib-bib16] H. Poincaré, Les méthodes nouvelles de la mécanique céleste. Tome I. Les Grands Classiques Gauthier-Villars, Paris (1892); reprint: Les Grands Classiques Gauthier-Villars, Lib. Sci. Tech. Albert Blanchard, Paris (1987)

[bib-bib17] H. Poincaré, Sur un théorème de géométrie. Rend. Circ. Mat. Palermo 33, 375–407 (1912)

[bib-bib18] J. Robbin and D. Salamon, The Maslov index for paths. Topology 32, 827–844 (1993)

[bib-bib19] L. Sloman, Geometers engineer new tools to wrangle spacecraft orbits. Quanta Magazine (2024) https://www.quantamagazine.org/geometers-engineer-new-tools-to-wrangle-spacecraft-orbits-20240415